计算机存储内部数据的原理，编程语言的发展史和分类，python解释器的下载和安装，计算机cmd窗口的使用，环境变量和解释器多版本共存方法

计算机内部存储数据的原理

计算机内部只认识01二进制.
存储单位:0和1分别代表一个比特位（bit）.8bit=1bytes(字节） 1024kb=1MB  1024MB=1GB  1024GB=1TB

编程语言的发展史

1.机器语言
机器能够直接识别出来的程序语言或着指令代码.优势:执行速度快直接执行资源占用少, 劣势:学习难度大编程繁杂.
2.汇编语言
用简单的字母代表一串二进制比如a，b，c，d将机器语言做了简单的编译.优势：执行速度快，劣势：学习难度大，推广和移植能力差.
3.高级语言
接近数学语言或者是人的自然语言.优势:学习难度大大降低，编程效率大大提高.劣势:执行速度相比较慢了.
'（注意高级语言的存在必须要有翻译官的存在进行翻译）'

编程语言的分类

1.编译型语言
 常见的语言:# C++，直接编译结果.优点:方便，劣势:不方便修改bug
2.解释型语言
常见的语言: # python.每执行一次都要翻译一次.优势:方便更改bug，劣势:执行效率低
'识别C++语言,安装C++编译器.识别python语言,安装python解释器'

python解释器的下载与安装

到官网：https://www.python.org/ 上下载.'根据自己的电脑系统选择系统'

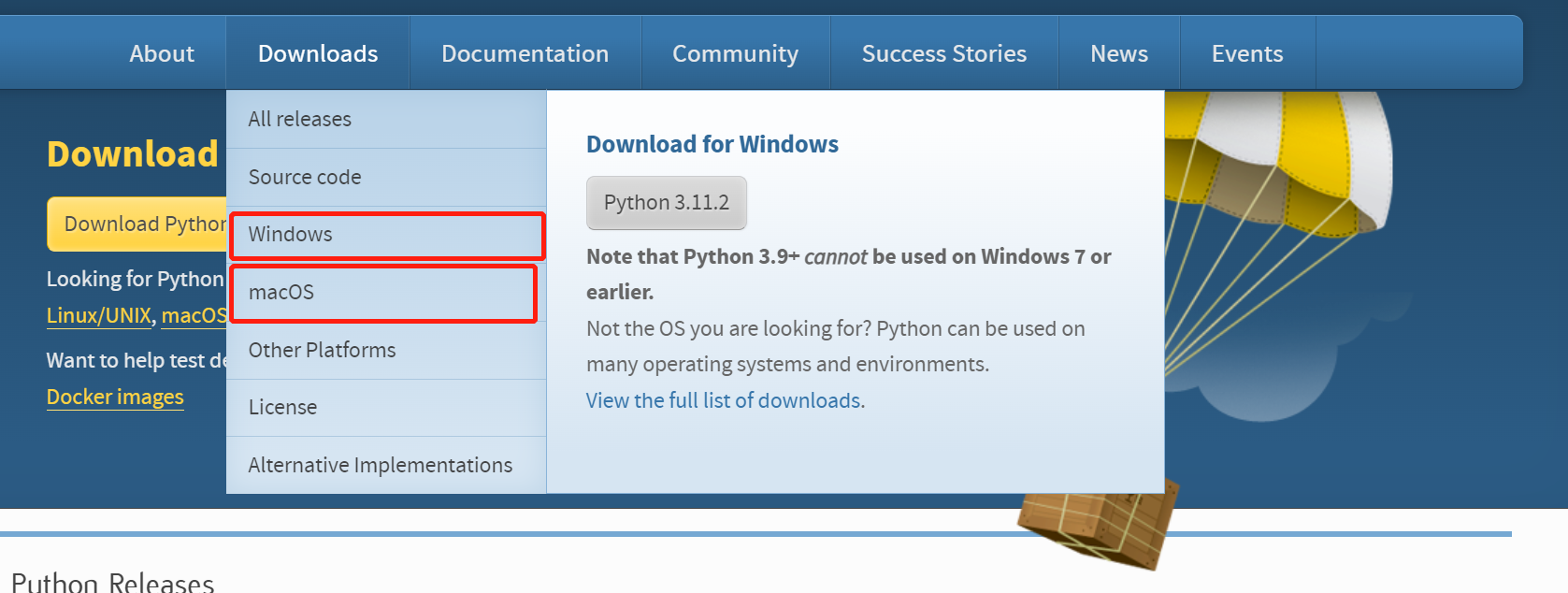
根据自己需要下载的版本选择对应的版本

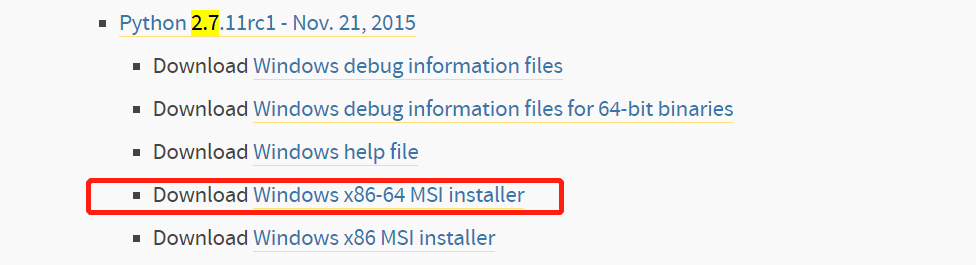
'''注意:安装之前如果已经安装了相同版本的解释器，要提前卸载，在安装，防止冲突（注意不要放入c盘中减小下路径）'''

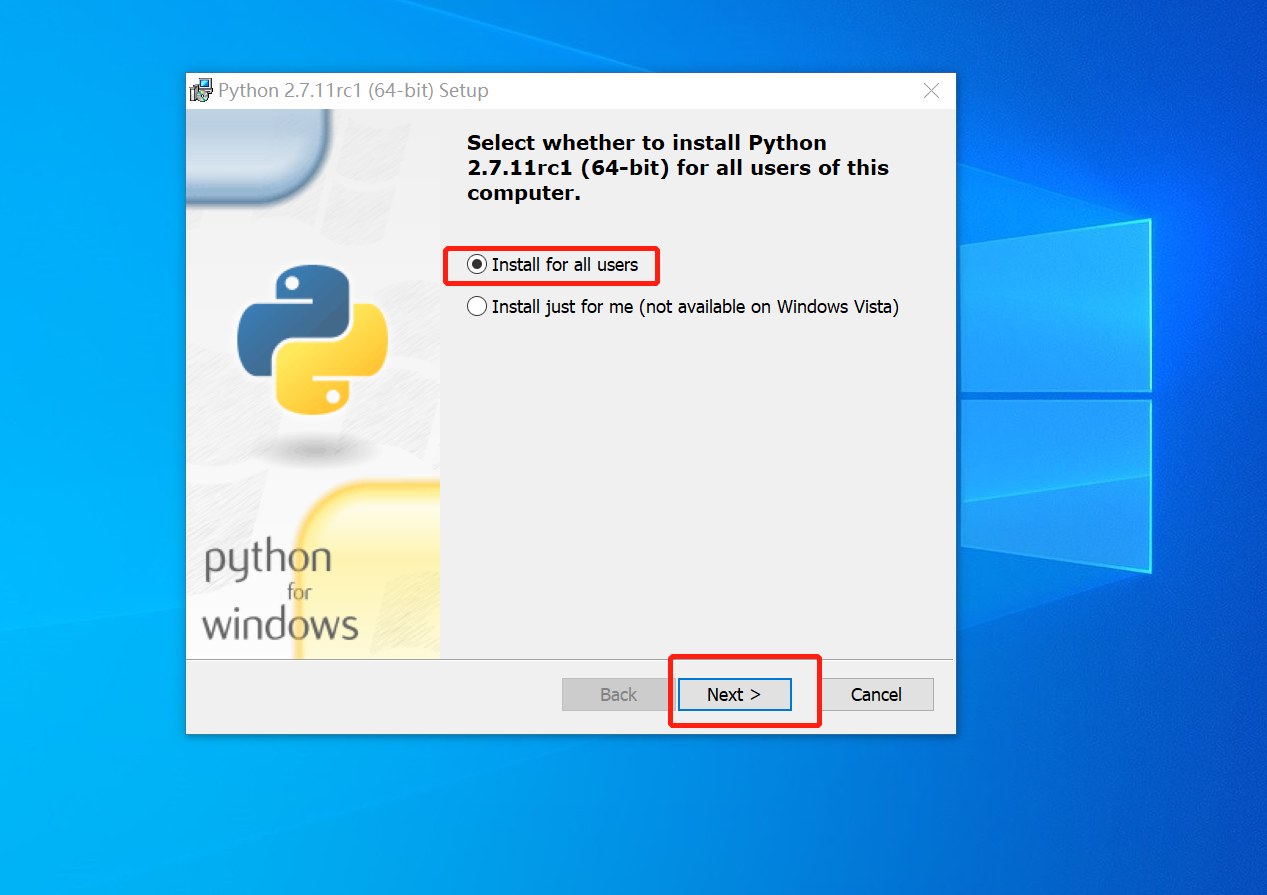
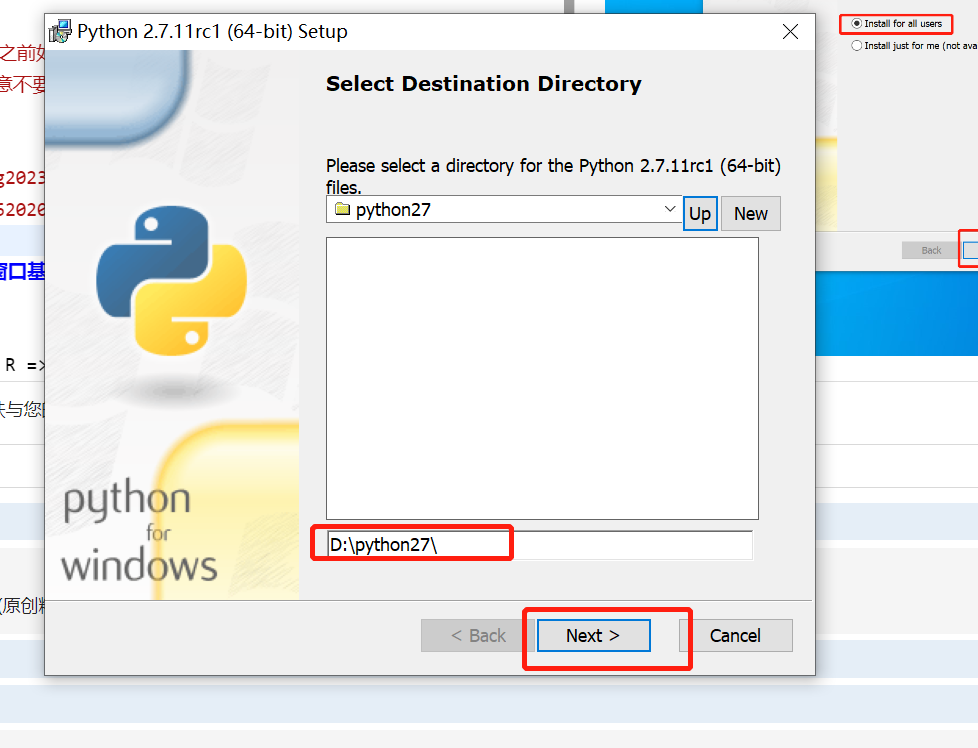
计算机cmd窗口基本使用

1.windows + R => 输入cmd即可进入运行

2.改变硬盘比如：'d加：'（要在英文状态下）

3按cd键再按空格加路径名称回车就切换了路径

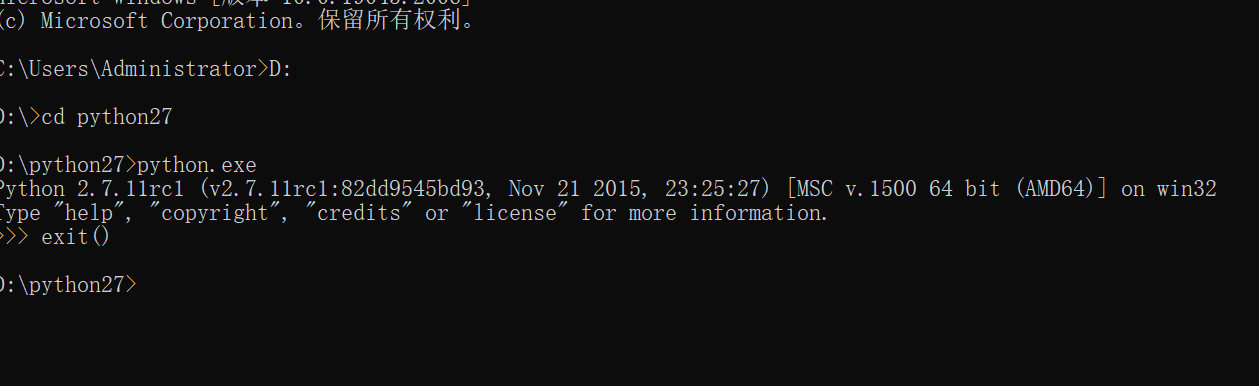
4.执行 python.exe进入python环境，退出python解释器：'exit()'

路径的基本概念

就是数据存储的位置
相对路径:需要拿一个参照物来参考，位置范围广概念不清晰不好找.
绝对路径：一个具体的位置只需要去这个位置就能找到.

环境变量

就是一个公共的仓库，右键此电脑，点击属性

打开高级系统设置

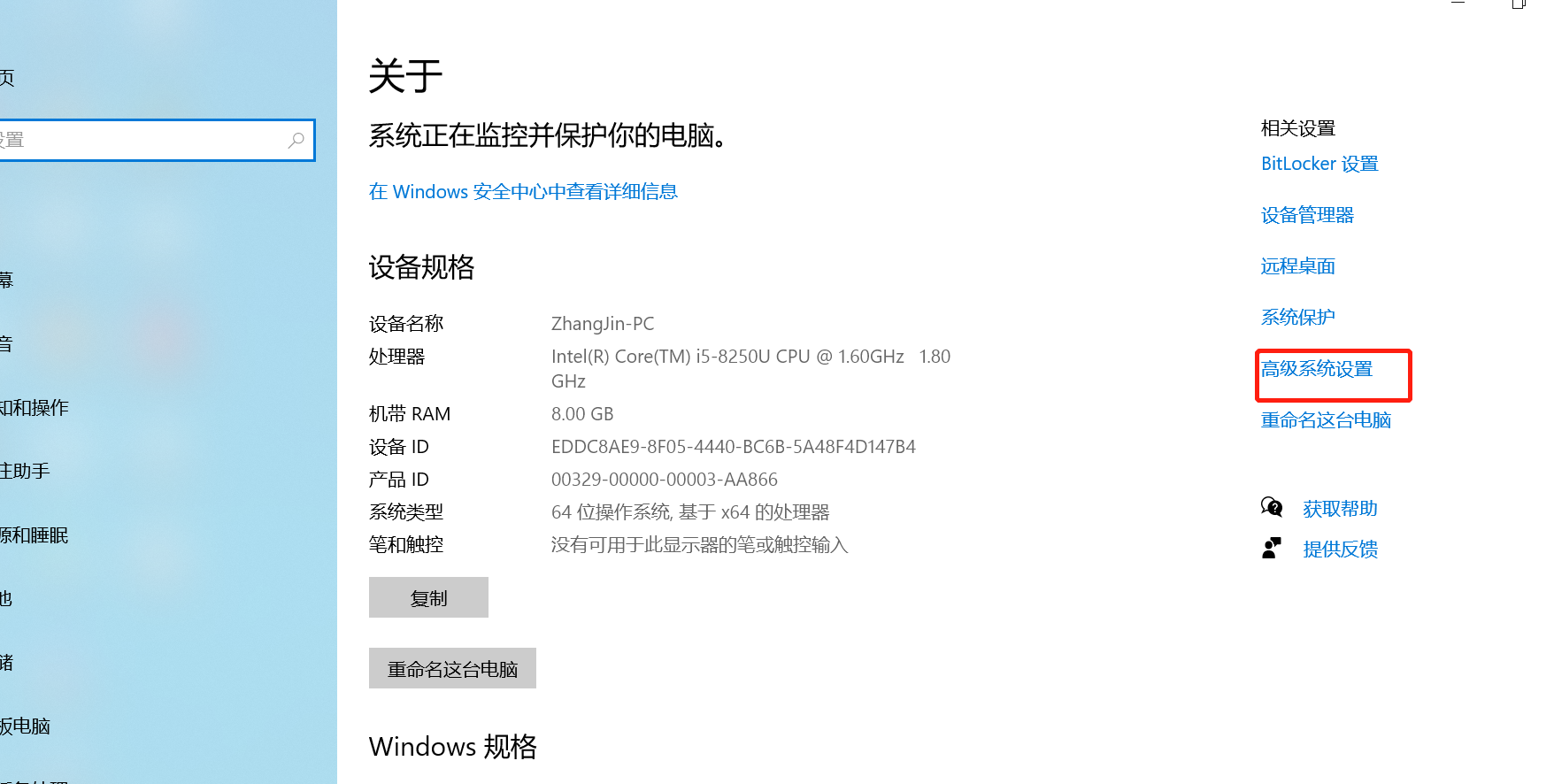
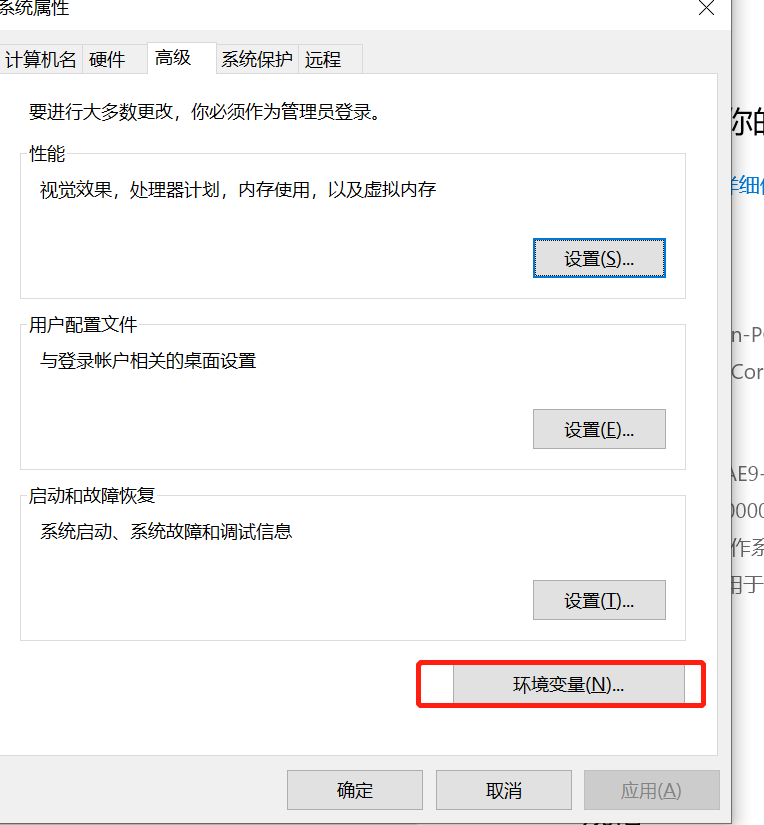
点开环境变量

选择Path（就是环境变量）选系统变量选项

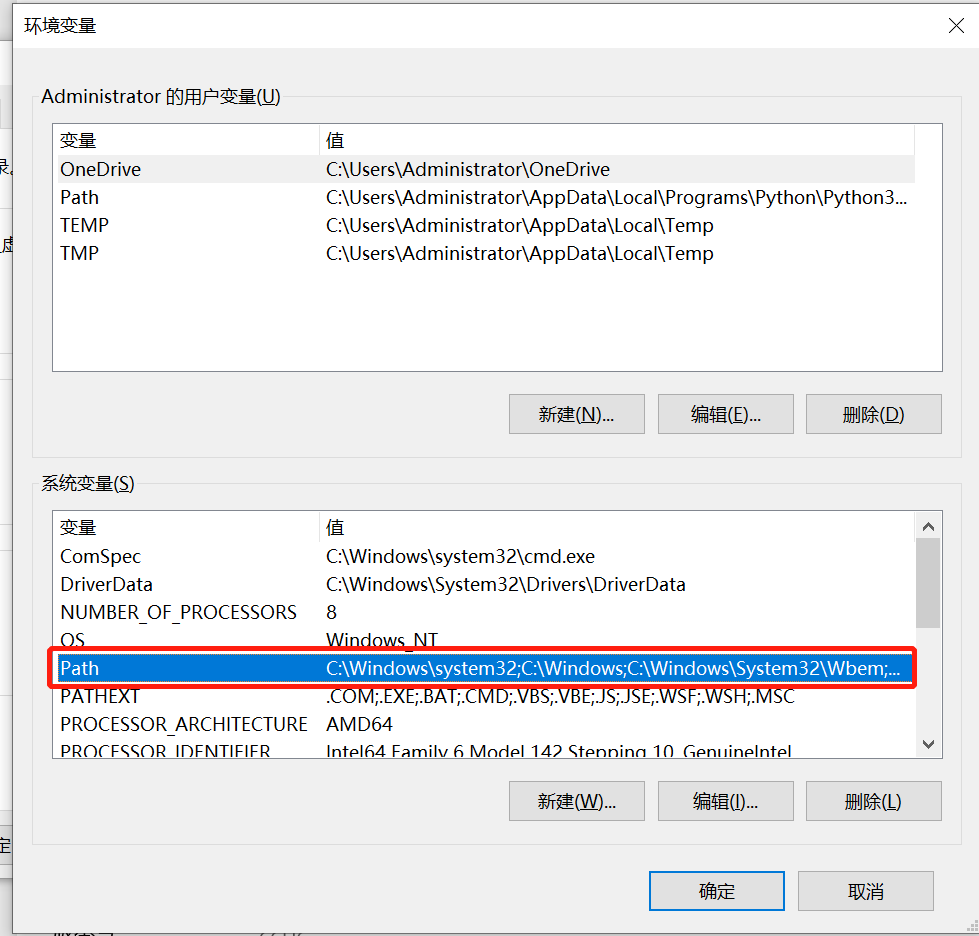
解释器多版本共存

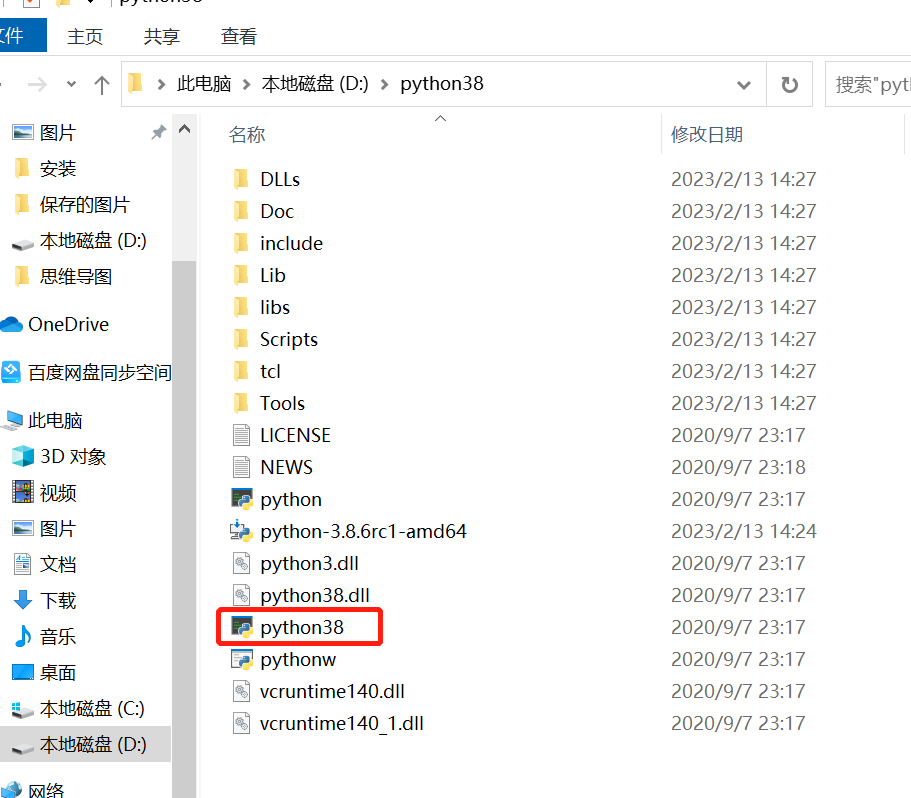
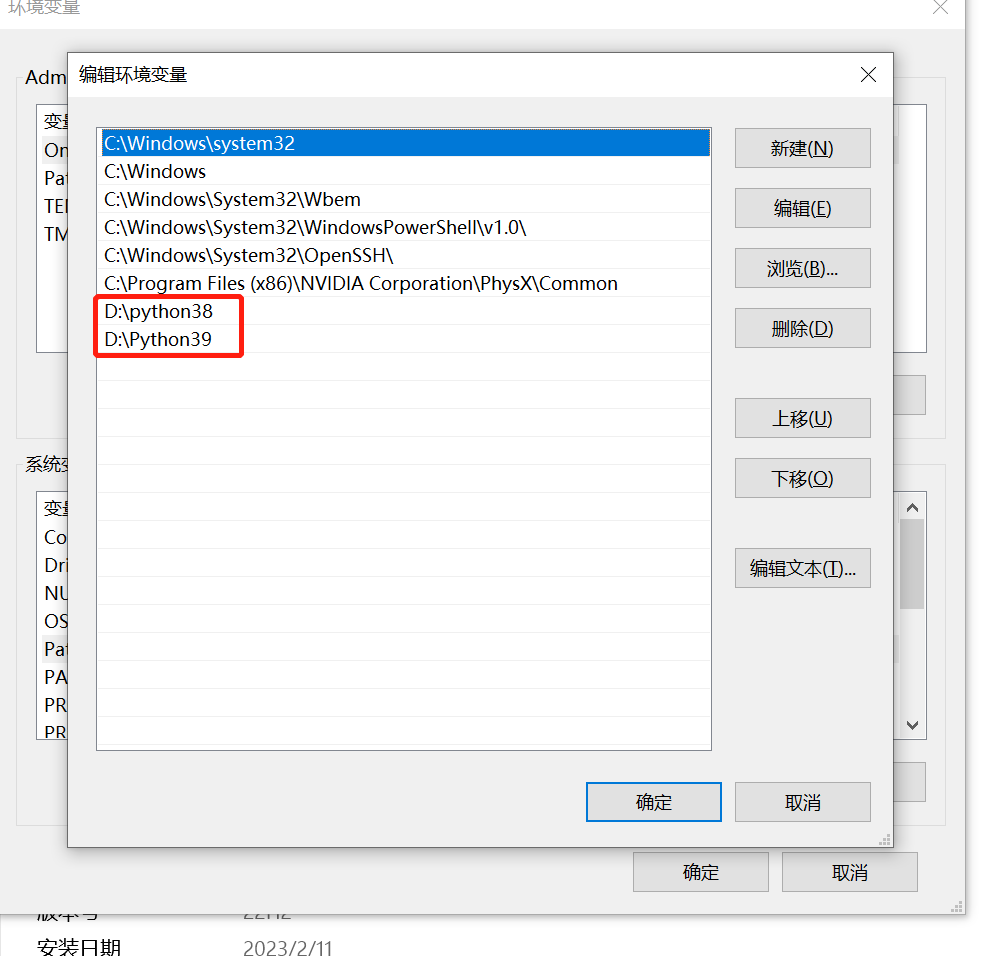
把每个解释器的路径放在在环境变量中，拷贝原来的python重命名为自己的名字比如python38.放两个解析器程序路径到path中形成多开版本共存.

第一个python程序

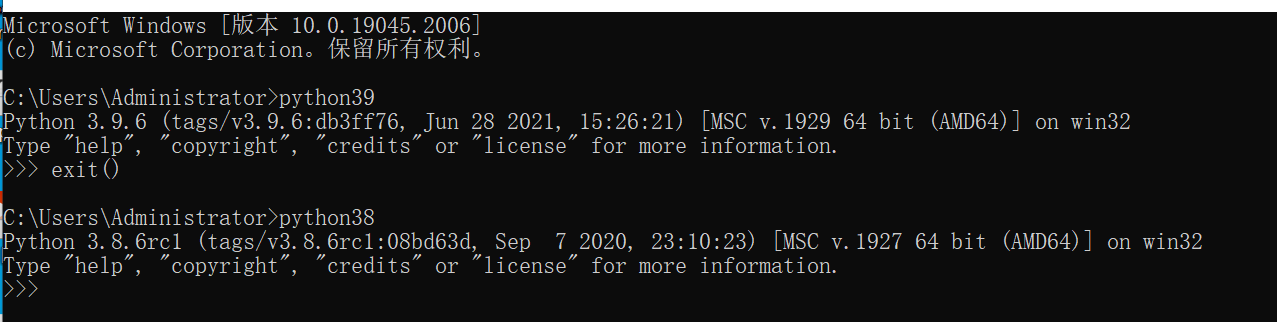
cmd窗口直接进入python环境（代码不能永久保存，没有代码提示功能）

通过解释器路径打开代码环境（可以永久保存代码，但是还是没有代码提示功能）

pycharm的下载

去https://www.jetbrains.com/pycharm/上下载根据系统下载