uva 1416 Warfare And Logistics

题意：

给出一个无向图，定义这个无向图的花费是

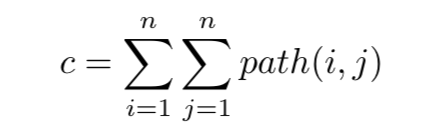
其中path(i,j)，是i到j的最短路。

去掉其中一条边之后，花费为c’，问c’ – c的最大值，输出c和c’。

思路：

枚举每条边，每次把这条边去掉，然后以每个点为起点，跑一次Dijkstra，再计算总花费。

这样的复杂度为O(mn^2log(n))，这个复杂度刚好卡着时间过，所以是暴力，更优的方法是最短路树（待学习。

代码：

 #include <stdio.h>
 #include <string.h>
 #include <vector>
 #include <queue>
 using namespace std;

 struct edge
 {
     int to,cost;
     int id;

     edge(int uu,int vv,int idd)
     {
         to = uu;
         cost = vv;
         id = idd;
     }
 };

 const int maxn = ;

 typedef pair<long long,int> pii;
 long long d[maxn];
 vector<edge> g[maxn];
 bool ma[];

 void adde(int st,int en,int cost,int id)
 {
     g[st].push_back(edge(en,cost,id));
 }

 void dij(int s,int n)
 {
     for (int i = ;i <= n;i++) d[i] = 1e16;

     priority_queue<pii,vector<pii>,greater<pii> > pq;

     pq.push(pii(,s));

     d[s] = ;

     //printf("***\n");

     while (!pq.empty())
     {
         pii x = pq.top();pq.pop();

         int v = x.second;

         if (d[v] < x.first) continue;

         for (int i = ;i < g[v].size();i++)
         {
             edge e = g[v][i];

             if (d[e.to] > d[v] + e.cost)
             {
                 d[e.to] = d[v] + e.cost;
                 pq.push(pii(d[e.to],e.to));
             }
         }
     }

     //printf("***\n");
 }

 void dijk(int s,int n)
 {
     for (int i = ;i <= n;i++) d[i] = 1e16;

     priority_queue<pii,vector<pii>,greater<pii> > pq;

     pq.push(pii(,s));

     d[s] = ;

     while (!pq.empty())
     {
         pii x = pq.top();pq.pop();

         int v = x.second;

         if (d[v] < x.first) continue;

         for (int i = ;i < g[v].size();i++)
         {
             edge e = g[v][i];

             if (ma[e.id]) continue;

             if (d[e.to] > d[v] + e.cost)
             {
                 d[e.to] = d[v] + e.cost;
                 pq.push(pii(d[e.to],e.to));
             }
         }
     }

     //printf("***\n");
 }

 int main()
 {
     int n,m,l;

     while (scanf("%d%d%d",&n,&m,&l) != EOF)
     {
         for (int i = ;i <= n;i++) g[i].clear();

         for (int i = ;i < m;i++)
         {
             int a,b,c;

             scanf("%d%d%d",&a,&b,&c);

             adde(a,b,c,i);
             adde(b,a,c,i);
         }

         long long ans = ;

         for (int i = ;i <= n;i++)
         {

             dij(i,n);

             for (int j = ;j <= n;j++)
             {
                 if (d[j] == 1e16) d[j] = l;
                 ans += d[j];
             }
         }

         long long res = ;
         long long tmp = ;

         for (int i = ;i < m;i++)
         {
             ma[i] = ;

             long long orz = ;

             for (int j = ;j <= n;j++)
             {
                 dijk(j,n);

                 for (int k = ;k <= n;k++)
                 {
                     if (d[k] == 1e16) d[k] = l;
                     orz += d[k];
                 }
             }

             if (orz - ans > tmp)
             {
                 res = orz;
                 tmp = orz - ans;
             }

             ma[i] = ;
         }

         printf("%lld %lld\n",ans,res);
     }

     return ;
 }