Luogu P3616 【富金森林公园】

我们首先考虑一块石头高度变化对每个高度的查询的答案的影响，

即我们要记录，对于每个高度的查询的答案

所以要离散化高度（不然哪开的下数组啊）

不难发现，一次变化的对于不同高度的影响，对于一段连续高度是相同的

即一次修改操作，对于一段连续高度的答案，影响相同，满足区间修改性质

就决定是你了，树状数组

具体来说，考虑修改位置修改前后和两边的高度关系

但是情况很多，不妨把修改操作换成先删除（把高度降为0），再插入

考虑删除，插入的话，反过来就好，中间的是删除位置

情况1：中间比两边低

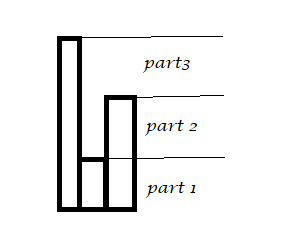
最简单的情况，不难发现，删除掉中间的只能让高度为$part1$的区间的答案$+1$，因为它割裂了两边的连续区间

情况2：中间比两边高

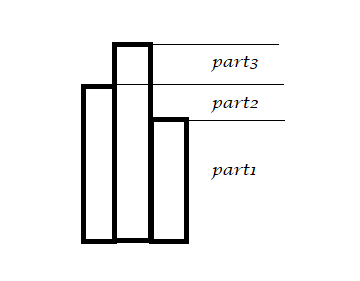
最高的区间影响就很广了

对于$part1:$它的删除会割裂两边的区间$val~of~part1++$

对于$part2:$因为两边没有构成连续区间，所以没有影响

对于$part3:$原来是有露出来的，现在没了，当然要减掉了

情况3：中间的高度也中等

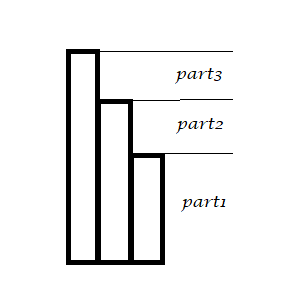
也很简单了，只对$part1$有影响

然而这样处理的只是答案的变化，我们还需要统计初始答案

还是考虑高度变化对答案的影响，不难发现，随着高度上升，未被覆盖的点的个数是单调不升的

按高度开$vector$，把每个高度恰好被覆盖的所有位置扔进去

从小到大枚举高度，先将这个高度的答案设为上一个高度的答案，取出这个高度恰好被覆盖的所有位置，统计这个位置的影响

如果它比两边高，类比上面情况2，答案减一

低呢，答案加一

这样我们就解决了这个问题

上代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn=2e5+;
vector<int>v[*maxn];
int pre[*maxn],n,m,a[maxn],mp[*maxn],op[maxn],cnt,b[maxn],d[maxn],c[*maxn];
bool vis[*maxn];
int lowbit(int x)
{
    return x&-x;
}
int sum(int x)
{
    int ret=;
    while(x)
    {
        ret+=c[x];
        x-=lowbit(x);
    }
    return ret;
}
void add(int x,int ch)
{
    while(x<=cnt)
    {
        c[x]+=ch;
        x+=lowbit(x);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
        mp[++cnt]=a[i];
    }
    for(int i=;i<=m;i++)
    {
        scanf("%d",&op[i]);
        if(op[i]==)
            scanf("%d",&b[i]),mp[++cnt]=b[i];
        else
            scanf("%d%d",&d[i],&b[i]),mp[++cnt]=b[i];
    }
    sort(mp+,mp+cnt+);
    cnt=unique(mp+,mp+cnt+)-mp-;
    for(int i=;i<=n;i++)
    {
        a[i]=lower_bound(mp+,mp+cnt+,a[i])-mp;
        v[a[i]+].push_back(i);
    }
    for(int i=;i<=m;i++)
        b[i]=lower_bound(mp+,mp+cnt+,b[i])-mp;
    pre[]=,vis[]=vis[n+]=;
    for(int i=;i<=cnt;i++)
    {
        pre[i]=pre[i-];
        for(int j=;j<v[i].size();j++)
        {
            int u=v[i][j];
            vis[u]=;
            if(!vis[u-]&&!vis[u+])
                pre[i]++;
            else if(vis[u-]&&vis[u+])
                pre[i]--;
        }
    }
    for(int i=;i<=m;i++)
    {
        if(op[i]==)
            printf("%d\n",pre[b[i]]+sum(b[i]));
        else
        {
            int tmp[];
            tmp[]=a[d[i]-],tmp[]=a[d[i]],tmp[]=a[d[i]+];
            sort(tmp+,tmp+);
            if(a[d[i]]>=a[d[i]-]&&a[d[i]]>=a[d[i]+])
                add(tmp[]+,-),add(tmp[]+,);
            add(,),add(tmp[]+,-);
            tmp[]=a[d[i]-],tmp[]=b[i],tmp[]=a[d[i]+];
            sort(tmp+,tmp+);
            if(b[i]>=a[d[i]-]&&b[i]>=a[d[i]+])
                add(tmp[]+,),add(tmp[]+,-);
            add(,-),add(tmp[]+,);
            a[d[i]]=b[i];
        }
    }
    return ;
}