Codeforces 700B Connecting Universities - 贪心

Treeland is a country in which there are n towns connected by n - 1 two-way road such that it's possible to get from any town to any other town.

In Treeland there are 2k universities which are located in different towns.

Recently, the president signed the decree to connect universities by high-speed network.The Ministry of Education understood the decree in its own way and decided that it was enough to connect each university with another one by using a cable. Formally, the decree will be done!

To have the maximum sum in the budget, the Ministry decided to divide universities into pairs so that the total length of the required cable will be maximum. In other words, the total distance between universities in k pairs should be as large as possible.

Help the Ministry to find the maximum total distance. Of course, each university should be present in only one pair. Consider that all roads have the same length which is equal to 1.

Input

The first line of the input contains two integers n and k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ n / 2) — the number of towns in Treeland and the number of university pairs. Consider that towns are numbered from 1 to n.

The second line contains 2k distinct integers u1, u2, ..., u2k (1 ≤ ui ≤ n) — indices of towns in which universities are located.

The next n - 1 line contains the description of roads. Each line contains the pair of integers xj and yj (1 ≤ xj, yj ≤ n), which means that the j-th road connects towns xj and yj. All of them are two-way roads. You can move from any town to any other using only these roads.

Output

Print the maximum possible sum of distances in the division of universities into k pairs.

Examples

input

7 2
1 5 6 2
1 3
3 2
4 5
3 7
4 3
4 6

output

6

input

9 3
3 2 1 6 5 9
8 9
3 2
2 7
3 4
7 6
4 5
2 1
2 8

output

9

Note

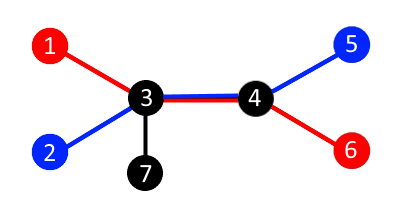
The figure below shows one of possible division into pairs in the first test. If you connect universities number 1 and 6 (marked in red) and universities number 2 and 5 (marked in blue) by using the cable, the total distance will equal 6 which will be the maximum sum in this example.

---

　　题目大意 给定一个边权都为1的无向连通图，和2k个点，将这2k个点两两进行配对，将每对的距离求和，问最大的距离和是多少？

　　首先看在最优的配对方案有没有什么规律，然而发现并没有。

　　既然不能快速地搞定最优配对方案，那可以考虑每个点连向父节点的边。

　　用f[i][j]表示第i个点，在第i个点的子树内有j个点还没有完成配对对答案的贡献。

　　转移是什么？+j。这个诡异的转移肯定有问题。

　　由于+j转移对后面的状态没有什么限制，所以开始贪心。。

　　显然在i的子树内没有完成配对的点数越多越好，当然要合法，所以就将i子树内被钦定的点数和剩余的被钦定的点数取最小值，然后直接加给答案。

Code

 /**
  * Codeforces
  * Problem#400B
  * Accepted
  * Time: 62ms
  * Memory: 13480k
  */
 #include <iostream>
 #include <fstream>
 #include <sstream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <ctime>
 #include <cmath>
 #include <cctype>
 #include <algorithm>
 #include <map>
 #include <set>
 #include <queue>
 #include <stack>
 #include <vector>
 #include <bitset>
 #ifdef WIN32
 #define Auto "%I64d"
 #else
 #define Auto "%lld"
 #endif
 using namespace std;
 typedef bool boolean;
 #define ll long long
 #define smin(_a, _b) _a = min(_a, _b)
 #define smax(_a, _b) _a = max(_a, _b)
 const signed int inf = (signed) (~0u >> );
 const signed ll llf = (signed ll) (~0ull >> );

 template<typename T>
 inline void readInteger(T& u) {
     static char x;
     while(!isdigit(x = getchar()));
     for(u = x - ''; isdigit(x = getchar()); u = u *  + x - '');
 }

 typedef class Edge {
     public:
         int end;
         Edge* next;

         Edge(int end = , Edge* next = NULL):end(end), next(next) {        }
 }Edge;

 typedef class MapManager {
     public:
         int ce;
         Edge **h;
         Edge *edge;

         MapManager() {    }
         MapManager(int n, int m):ce() {
             h = new Edge*[(n + )];
             edge = new Edge[(m + )];
             memset(h, , sizeof(Edge*) * (n + ));
         }

         void addEdge(int u, int v) {
             edge[ce] = Edge(v, h[u]);
             h[u] = edge + (ce++);
         }

         void addDoubleEdge(int u, int v) {
             addEdge(u, v);
             addEdge(v, u);
         }

         Edge* start(int node) {
             return h[node];
         }
 }MapManager;

 int n, m;
 boolean* isspy;
 MapManager g;

 inline void init() {
     readInteger(n);
     readInteger(m);
     m <<= ;
     isspy = new boolean[(n + )];
     g = MapManager(n,  * n);
     memset(isspy, false, sizeof(boolean) * (n + ));
     for(int i = , x; i <= m; i++) {
         readInteger(x);
         isspy[x] = true;
     }
     for(int i = , u, v; i < n; i++) {
         readInteger(u);
         readInteger(v);
         g.addDoubleEdge(u, v);
     }
 }

 ll res = ;
 int dfs(int node, int fa) {
     int rt = isspy[node];
     for(Edge* it = g.start(node); it; it = it->next) {
         if(it->end == fa)    continue;
         rt += dfs(it->end, node);
     }
     res += min(m - rt, rt);
     return rt;
 }

 inline void solve() {
     dfs(, );
     printf(Auto, res);
 }

 int main() {
     init();
     solve();
     return ;
 }