KMeans (K均值)算法讲解及实现

算法原理

---

KMeans算法是典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。
K个初始聚类中心点的选取对聚类结果具有较大的影响，因为在该算法第一步中是随机地选取任意k个对象作为初始聚类中心，初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象，根据其与各个簇中心的距离赋给最近的簇。当考查完所有数据对象后，一次迭代运算完成，新的聚类中心被计算出来。
算法过程如下：
（1）从N个数据文档（样本）随机选取K个数据文档作为质心（聚类中心）。
本文在聚类中心初始化实现过程中采取在样本空间范围内随机生成K个聚类中心。
（2）对每个数据文档测量其到每个质心的距离，并把它归到最近的质心的类。
（3）重新计算已经得到的各个类的质心。
（4）迭代（2）~（3步直至新的质心与原质心相等或小于指定阈值，算法结束。
本文采用所有样本所属的质心都不再变化时，算法收敛。

代码实现

---

本文在实现过程中采用数据集4k2_far.txt，聚类算法实现过程中默认的类别数量为4。

(1)辅助函数myUtil.py

# -*- coding:utf-8 -*-
from numpy import *

# 数据文件转矩阵
# path： 数据文件路径
# delimiter: 行内字段分隔符
def file2matrix(path, delimiter):
    fp = open(path, "rb")   # 读取文件内容
    content = fp.read()
    fp.close()
    rowlist = content.splitlines()   # 按行转换为一维表
    # 逐行遍历，结果按分隔符分隔为行向量
    recordlist = [map(eval, row.split(delimiter)) for row in rowlist if row.strip()]
    # 返回转换后的矩阵形式
    return mat(recordlist)

# 随机生成聚类中心
def randCenters(dataSet, k):
    n = shape(dataSet)[1]   # 列数
    clustercents = mat(zeros((k, n)))   # 初始化聚类中心矩阵：k*n
    for col in xrange(n):
        mincol = min(dataSet[:, col])
        maxcol = max(dataSet[:, col])
        # random.rand(k, 1):产生一个0~1之间的随机数向量（k,1表示产生k行1列的随机数）
        clustercents[:, col] = mat(mincol + float(maxcol - mincol) * random.rand(k, 1))   # 按列赋值
    return clustercents

# 欧式距离计算公式
def distEclud(vecA, vecB):
    return linalg.norm(vecA-vecB)

# 绘制散点图
def drawScatter(plt, mydata, size=20, color='blue', mrkr='o'):
    plt.scatter(mydata.T[0], mydata.T[1], s=size, c=color, marker=mrkr)

# 以不同颜色绘制数据集里的点
def color_cluster(dataindx, dataSet, plt):
    datalen = len(dataindx)
    for indx in xrange(datalen):
        if int(dataindx[indx]) == 0:
            plt.scatter(dataSet[indx, 0], dataSet[indx, 1], c='blue', marker='o')
        elif int(dataindx[indx]) == 1:
            plt.scatter(dataSet[indx, 0], dataSet[indx, 1], c='green', marker='o')
        elif int(dataindx[indx]) == 2:
            plt.scatter(dataSet[indx, 0], dataSet[indx, 1], c='red', marker='o')
        elif int(dataindx[indx]) == 3:
            plt.scatter(dataSet[indx, 0], dataSet[indx, 1], c='cyan', marker='o')

(2)KMeans实现核心函数kmeans.py

from myUtil import *

def kMeans(dataSet, k):
    m = shape(dataSet)[0]  # 返回矩阵的行数

    # 本算法核心数据结构:行数与数据集相同
    # 列1：数据集对应的聚类中心,列2:数据集行向量到聚类中心的距离
    ClustDist = mat(zeros((m, 2)))

    # 随机生成一个数据集的聚类中心:本例为4*2的矩阵
    # 确保该聚类中心位于min(dataSet[:,j]),max(dataSet[:,j])之间
    clustercents = randCenters(dataSet, k)  # 随机生成聚类中心

    flag = True  # 初始化标志位,迭代开始
    counter = []  # 计数器

    # 循环迭代直至终止条件为False
    # 算法停止的条件：dataSet的所有向量都能找到某个聚类中心,到此中心的距离均小于其他k-1个中心的距离
    while flag:
        flag = False  # 预置标志位为False

        # ---- 1. 构建ClustDist： 遍历DataSet数据集,计算DataSet每行与聚类的最小欧式距离 ----#
        # 将此结果赋值ClustDist=[minIndex,minDist]
        for i in xrange(m):

            # 遍历k个聚类中心,获取最短距离
            distlist = [distEclud(clustercents[j, :], dataSet[i, :]) for j in range(k)]
            minDist = min(distlist)
            minIndex = distlist.index(minDist)

            if ClustDist[i, 0] != minIndex:  # 找到了一个新聚类中心
                flag = True  # 重置标志位为True，继续迭代

            # 将minIndex和minDist**2赋予ClustDist第i行
            # 含义是数据集i行对应的聚类中心为minIndex,最短距离为minDist
            ClustDist[i, :] = minIndex, minDist

        # ---- 2.如果执行到此处，说明还有需要更新clustercents值: 循环变量为cent(0~k-1)----#
        # 1.用聚类中心cent切分为ClustDist，返回dataSet的行索引
        # 并以此从dataSet中提取对应的行向量构成新的ptsInClust
        # 计算分隔后ptsInClust各列的均值，以此更新聚类中心clustercents的各项值
        for cent in xrange(k):
            # 从ClustDist的第一列中筛选出等于cent值的行下标
            dInx = nonzero(ClustDist[:, 0].A == cent)[0]
            # 从dataSet中提取行下标==dInx构成一个新数据集
            ptsInClust = dataSet[dInx]
            # 计算ptsInClust各列的均值: mean(ptsInClust, axis=0):axis=0 按列计算
            clustercents[cent, :] = mean(ptsInClust, axis=0)
    return clustercents, ClustDist

(3)KMeans算法运行主函数kmeans_test.py

# -*- encoding:utf-8 -*-

from kmeans import *
import matplotlib.pyplot as plt

dataMat = file2matrix("testData/4k2_far.txt", "\t")   # 从文件构建的数据集
dataSet = dataMat[:, 1:]   # 提取数据集中的特征列

k = 4   # 外部指定1,2,3...通过观察数据集有4个聚类中心
clustercents, ClustDist = kMeans(dataSet, k)

# 返回计算完成的聚类中心
print "clustercents:\n", clustercents

# 输出生成的ClustDist：对应的聚类中心(列1),到聚类中心的距离(列2),行与dataSet一一对应
color_cluster(ClustDist[:, 0:1], dataSet, plt)
# 绘制聚类中心
drawScatter(plt, clustercents, size=60, color='red', mrkr='D')
plt.show()

评估分类结果

---

（1）正确的分类输出
KMeans聚类结果如图所示：

Kmeans分类正确结果

输出的聚类中心结果如下：

clustercents:
[[ 6.99438039  5.05456275]
 [ 8.08169456  7.97506735]
 [ 3.02211698  6.00770189]
 [ 2.95832148  2.98598456]]

（2）错误输出

因为聚类中心随机初始化的关心，KMeans并不是总能够找到正确的聚类，下面是不能找到正确分类的情况。

情况一，局部最优收敛：

clustercents:
[[ 2.9750599   3.77881139]
 [ 7.311725    5.00685   ]
 [ 6.7122963   5.09697407]
 [ 8.08169456  7.97506735]]

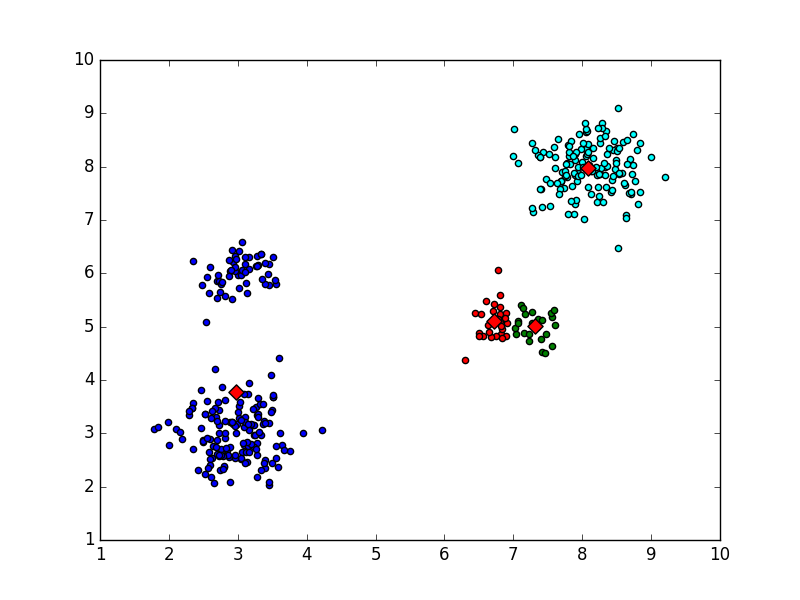
Kmeans错误分类结果一

情况二，只收敛到三个聚类中心：

clustercents:
[[ 6.99438039  5.05456275]
 [ 2.9750599   3.77881139]
 [ 8.08169456  7.97506735]
 [        nan         nan]]

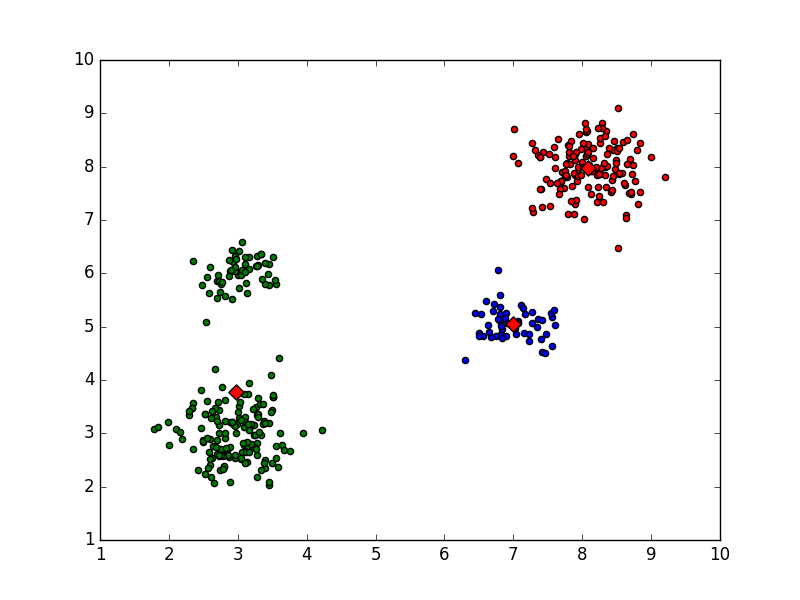
Kmeans错误分类结果二

KMeans算法适用场景及优缺点

---

KMeans擅长处理球状分布的数据，当结果聚类是密集的，而且类和类之间的区别比较明显时，K均值的效果比较好。对于处理大数据集，这个算法是相对可伸缩的和高效的，它的复杂度是O(nkt),n是对象的个数，k是簇的数目，t是迭代的次数。相比其他的聚类算法，KMeans比较简单、容易掌握，这也是其得到广泛使用的原因之一。
但KMeans算法也存在一些问题。
（1）算法的初始中心点选择与算法的运行效率密切相关，而随机选取中心点有可能导致迭代次数很大或者限于某个局部最优状态；通常k<<n,且t<<n，所以算法经常以局部最优收敛。
（2）K均值的最大问题是要求用户必须事先给出k的个数，k的选择一般都基于一些经验值和多次试验的结果，对于不同的数据集，k的取值没有可借鉴性。
（3）对异常偏离的数据敏感——离群点；K均值对“噪声”和孤立点数据是敏感的，少量的这类数据就能对平均值造成极大的影响。

因此，提出了二分KMeans算法，用以改进KMeans算法局部最优的问题。

相关

---

1、：Bisecting KMeans (二分K均值)算法讲解及实现。