BZOJ.4543.[POI2014]Hotel加强版(长链剖分 树形DP)

题目链接

弱化版：https://www.cnblogs.com/SovietPower/p/8663817.html。

令\(f[x][i]\)表示\(x\)的子树中深度为\(i\)的点的个数，\(g[x][i]\)表示\(x\)子树中，满足\(u,v\)到\(LCA(u,v)\)的距离都是\(d\)，且到\(x\)的距离为\(d-i\)的点对\((u,v)\)个数。（就是不以\(x\)作为三个点的中心位置，那样就没法算了）

如图


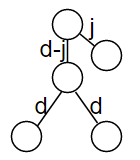
那么就可以由\(g[x][i]\)与另一棵子树的\(f[y][i-1]\)，以及\(g[x][0]\)更新答案。

\(f\)的转移简单。\(g[x][i]\)要么是从某个子树中得到(\(g[x][i]+=g[v][i+1]\))，要么是以x作为LCA从某两个子树中得到(\(g[x][i]+=f[x][i]*f[v][i-1]\))。

直接这样复杂度\(O(n^2)\)。

DP数组的下标都是深度，所以可以用长链剖分。继承重儿子时\(f\)需要右移，\(g\)需要左移，还是用指针方便些吧（\(g\)的前后都需要留空间）。

复杂度\(O(n)\)。

为啥洛谷上跑的不快啊(30ms)==没道理啊。

//7788kb	376ms
#include <cstdio>
#include <cctype>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=1e5+5;

int Enum,H[N],nxt[N<<1],to[N<<1],dep[N],mxd[N],son[N],pos[N],*f[N],Fp[N],*fp=Fp;
LL Ans,*g[N],Gp[N<<1],*gp=Gp;
char IN[MAXIN],*SS=IN,*TT=IN;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline void AE(int u,int v)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum;
	to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum;
}
inline void Allot(int x)
{
	f[x]=fp, fp+=mxd[x], gp+=mxd[x], g[x]=gp, gp+=mxd[x];
}
void DFS1(int x,int fa)
{
	int mx=0;
	for(int i=H[x],v; i; i=nxt[i])
		if((v=to[i])!=fa) dep[v]=dep[x]+1, DFS1(v,x), mxd[v]>mx&&(mx=mxd[v],son[x]=v);
	mxd[x]=mx+1;
//	for(int i=H[x],v; i; i=nxt[i])
//		if((v=to[i])!=fa) dep[v]=dep[x]+1, DFS1(v,x), mxd[v]>mxd[son[x]]&&(son[x]=v);
//	mxd[x]=mxd[son[x]]+1;
}
void DFS2(int x,int fa)
{
	if(son[x]) f[son[x]]=f[x]+1, g[son[x]]=g[x]-1, DFS2(son[x],x);
	f[x][0]=1, Ans+=g[x][0];//重儿子子树与x的贡献
	for(int i=H[x],v; i; i=nxt[i])
		if((v=to[i])!=fa&&v!=son[x])
		{
			Allot(v), DFS2(v,x); int l=mxd[v];
			for(int j=1; j<=l; ++j) Ans+=g[x][j]*f[v][j-1]+g[v][j]*f[x][j-1];
			for(int j=1; j<=l; ++j) g[x][j]+=g[v][j+1]+1ll*f[x][j]*f[v][j-1],f[x][j]+=f[v][j-1];//g[x][0]转移来也没啥用啊
		}
}

int main()
{
	int n=read();
	for(int i=1; i<n; ++i) AE(read(),read());
	DFS1(1,1), Allot(1), DFS2(1,1);
	printf("%lld\n",Ans);

	return 0;
}