编码器AE & VAE

学习总结于国立台湾大学 ：李宏毅老师

自编码器 AE (Auto-encoder)    &　变分自动编码器VAE(Variational Auto－encoder)

                  

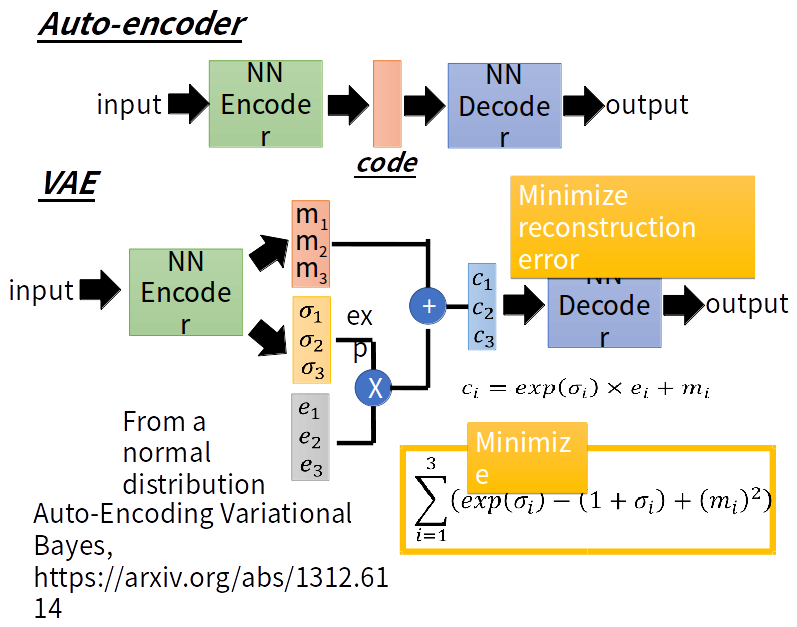
学习编码解码过程，然后任意输入一个向量作为code通过解码器生成一张图片。

VAE与AE的不同之处是：VAE的encoder产生与noise作用后输入到decoder

          

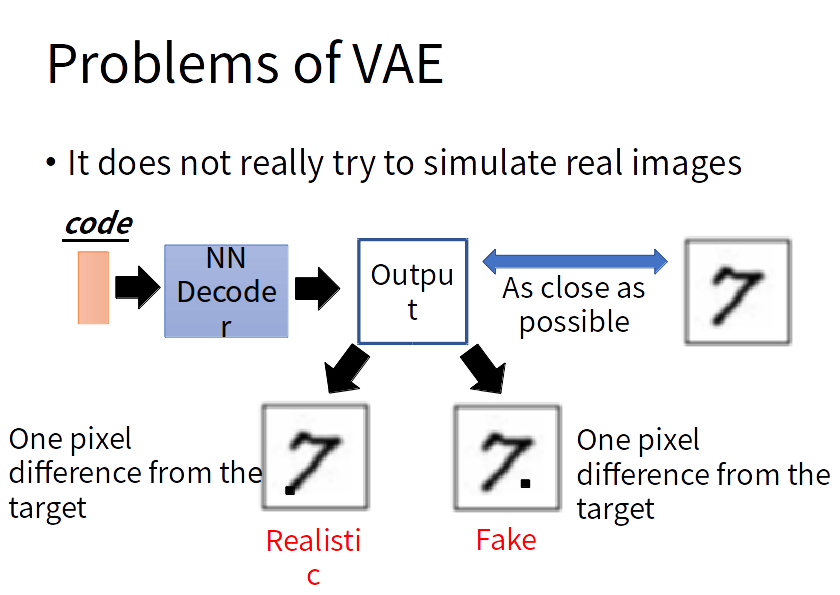
VAE的问题：VAE的decoder的输出与某一张越接近越好，但是对于机器来说并没有学会自己产生realistic的image。它只会模仿产生的图片和database里面的越像越好，而不会产生新的图片。

Why VAE？

intuitive reason：

                           

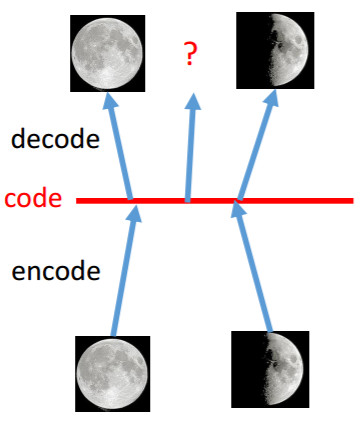
AE的过程                                                                            VAE的过程

这时给定满月与弦月之间的code，AE会得到什么？可能得到一个根本就不是月亮的东西。对于VAE，满月的code在一个noise的影响下仍然需要恢复为满月，弦月的code在一个noise的影响下仍然需要恢复为弦月。那么交集部分应该即为满月有为弦月，但是只能输出一张图像，所以可能会输出一张介于满月、弦月的月像，所以可能会得到一张比AE有意义的图像。再看VAE的流程图。m为原来的code（original code）。c为加了noise的code（Code with noise）。noise的方差是自动学习来的。那如果让机器自己学，那肯定希望方差是0好了，即变为了AE，这时重构误差（reconstruction error）就是最小的。所以要强迫方差不可以太小，设定一个限制：

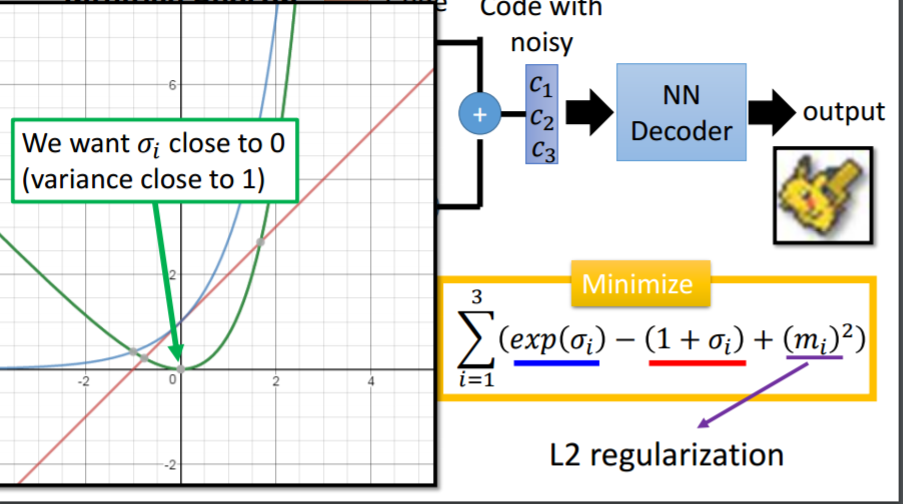
加上这个最小化限制以后，方差就接近于1，不会出现方差为0了。L2正则化减少过拟合，不会learn出太trivial的solution。以上是直观的理解。下面是理论理解：

假设P(x)为像Pokemon的概率，那么越像Pokemon，这个概率越大，否则概率越低。那如果我们可以estimate出这个分布也就结束了，那怎么estimate这个高维空间上的机率分布p(x)呢(注意x是一个vector，如果知道了p(x)的样子，就可以根据p(x)sample出一张图)？可以用高斯混合模型（gaussian mixture model）。

      

高斯混合模型

现在假设共有100个gaussian，那么这100个gaussian每个都有一个weight。要做的是根据每个gaussian的weight来决定先从哪个gaussian来sample data，然后再从你决定的那个gaussian来simple data。看下图: m为整数代表第几个gaussian。第m个gaussian服从高斯分布的参数为（μ_m, Σ_m）。所以P(x)为所有高斯的综合：

参数解释：

P(m)为第m个高斯的weight。

P(x|m)为有了这个高斯之后sample出x的几率。

z~N(0, I)是从一个normal distribution里面sample出来的。 z是一个vector，每个dimension代表你要sample东西的某种特质。根据z你可以决定高斯的（μ, Σ）。高斯混合中有几个高斯就有几个mean和variance：

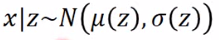
但是z是连续的，mean和variance是无穷多的，那么怎么给定一个z找到mean和variance呢？假设mean和variance都来自于一个function。那P(x)是怎样产生的呢？如下图：为方便假设z为一维，每个点都可能被sample到，只是中间可能性更大：

当你在z上sample出一个点后，它会对应于一个gaussian：

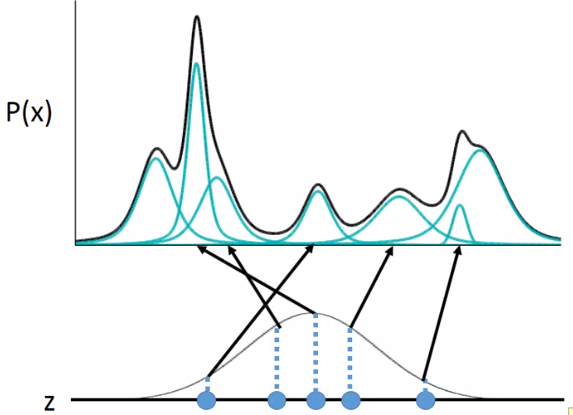
关键：至于哪个点对应到哪个gaussian呢，是由某个function所决定的。所以当你的高斯混合中的高斯是从一个normal distribution 产生的，那么就是相当于有无穷多的gaussian。一般可能高斯混合有512个高斯，那现在就可有无穷多的gaussian。那么又咋知道每个z对应到什么样的mean和variance呢？即这个function是咋样呢？我们知道NN就是一个function。这个function就是：

给定一个z输出两个vector，代表mean个variance。即这个function(NN)可以告诉我们在z上每个点对应到x的高斯混合上的mean合variance是多少。

那现在P(x)的样子就变了：

那z也不一定是gaussian，可以是任何东西。不用担心z的选择会影响P(x)的分布。因为NN的作用是很强大的。

所以现在问题很明朗：z为normal distribution， x|z ~N( μ(_z),  σ(_z) ),   μ(_z)和 σ(_z)是待去估计。那么就最大似然估计：x代表一个image：现在手上已经有的data（image），希望有一组mean和sigma的function可以让现在已有的data的P(x)取log后的和最大：

所以就是要调整NN的参数来最大化似然函数：

  Decoder

然后我们需要另一个分布 q(z|x): 给定x，输出z上的分布的mean和variance：

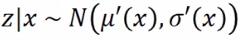
即这里也有一个function(NN),给定一个x输出z的一个mean和variance：

  Encoder

公式推导:

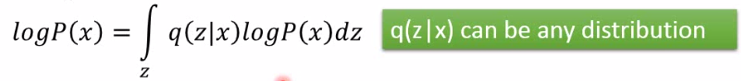
这里q(z|x)可以是任何一个分布，所以积分仍不变。恒等推导如下:

这样就找到了一个下界称为L_b 。之前只要找P(x|z),现在还要找q(z|x)来maximizing L_b。

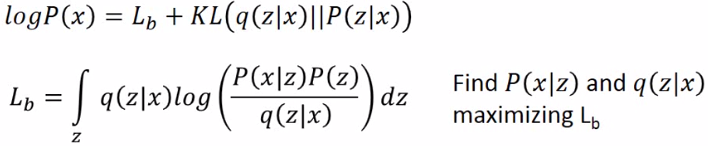
q(z|x)和p(z|x)将会越来越相近。

即最小化KL(q(z|x) || P(z))

 

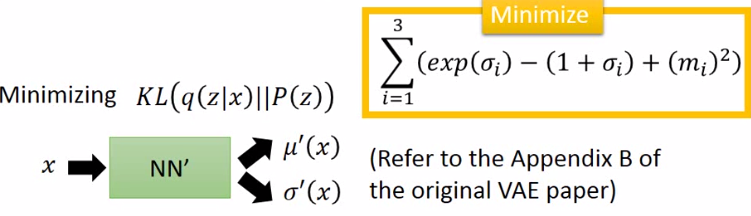
怎么最大似然呢？使得mean正好等于x：这也就是auto-encoder做的事情：

另：

VAE(Variational Autoencoder)的原理

变分自编码器（VAEs）

变分自编码器