内部排序->选择排序->树形选择排序

文字描述

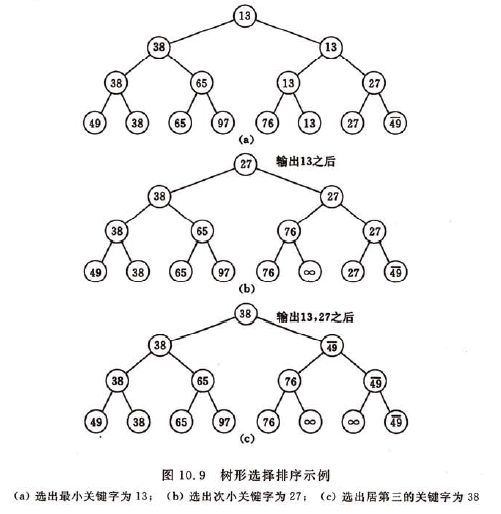
　　树形选择排序又称锦标赛排序; 比如,在8个运动员中决出前3名至多需要11场比赛, 而不是7+6+5=18场比赛(它的前提是甲胜乙，乙胜丙，则甲必能胜丙)

　　首先对n个记录的关键字进行两两比较，然后在(n/2)个较小者之间再进行两两比较，直至选出最小关键字的记录为止，这个过程可用一颗有n个叶子结点的完全二叉树表示。关于完全二叉树的定义和与本排序算法用到的性质见附录1

示意图

算法分析

　　由于含n个叶子结点的完全二叉树的深度为[log2n]+1, 则在树形选择排序中，除了最小关键字外，每选择一个次小关键字仅需进行log2n次比较，因此它的时间复杂度为nlogn.。但是它需要的辅助空间为2*n-1。而且它在选择过程中，和"最大值"进行了多余的比较。 另外，该算法是不稳定的。

代码实现

 #include <stdio.h>
 #include <stdlib.h>
 #include <math.h>
 /*
  * double log2(double x);    以2为底的对数
  * double ceil(double x);    取上整
  * double floor(double x);    取下整
  * double fabs(double x);    取绝对值
  */
 
 #define DEBUG
 
 #define EQ(a, b) ((a) == (b))
 #define LT(a, b) ((a) <  (b))
 #define LQ(a, b) ((a) <= (b))
 
 #define MAXSIZE  100
 #define INF         1000000
 typedef int KeyType;
 typedef char InfoType;
 typedef struct{
     KeyType key;
     InfoType otherinfo;
 }RedType;
 
 typedef struct{
     RedType r[MAXSIZE+];
     int length;
 }SqList;
 
 void PrintList(SqList L){
     int i = ;
     printf("下标值：");
     for(i=; i<=L.length; i++){
         printf("[%d] ", i);
     }
     printf("\n关键字：");
     for(i=; i<=L.length; i++){
         if(EQ(L.r[i].key, INF)){
             printf(" %-3c", '-');
         }else{
             printf(" %-3d", L.r[i].key);
         }
     }
     printf("\n其他值：");
     for(i=; i<=L.length; i++){
         printf(" %-3c", L.r[i].otherinfo);
     }
     printf("\n\n");
     return ;
 }
 
 /*树形选择排序算法*/
 void TreeSelectSort(SqList *L)
 {
     //为实现该排序所需的辅助树
     SqList tree;
     //辅助树的大小
     tree.length = L->length- + L->length;
 
     tree.r[].otherinfo = '';
     int i = , low = ;
     //由后向前填充此树的叶子结点
     for(i=; i<L->length; i++){
         tree.r[tree.length-i] = L->r[L->length-i];
     }
     //由后向前填充此树的非叶子结点
     for(i=(tree.length-L->length); i>=; i--){
         tree.r[i] = (LT(tree.r[*i].key, tree.r[*i+].key)?tree.r[*i]:tree.r[*i+]);
     }
     //纪录当前辅助树的最小结点
     RedType minred;
     //记录最小结点在叶子结点中的下标值
     int minindex = ;
     while(low <= L->length){
         minred = tree.r[];
 #ifdef DEBUG
         printf("第%d趟树形选择排序后，输出当前数最小值%d, %c\n", low, minred.key, minred.otherinfo);
         PrintList(tree);
 #endif
         //不断移走最小结点
         L->r[low++] = minred;
         minindex = tree.length;
         //找到最小值在辅助树叶子结点中的下标值
         for(minindex=tree.length; (minindex>(tree.length-L->length)); minindex--){
             if(EQ(tree.r[minindex].key, minred.key) && EQ(tree.r[minindex].otherinfo, minred.otherinfo)){
                 break;
             }
         }
         //设置一个最大值标志，INF表示无穷大
         tree.r[minindex].key = INF;
         //重新调整此辅助树，使根结点关键字值最小
         for(i=(minindex/); i>=; i/=){
             tree.r[i] = (LT(tree.r[*i].key, tree.r[*i+].key)?tree.r[*i]:tree.r[*i+]);
         }
     }
 #ifdef DEBUG
     printf("按照树形选择排序后的原顺序表：\n");
     PrintList(*L);
 #endif
 }
 
 int  main(int argc, char *argv[])
 {
     if(argc < ){
         return -;
     }
     SqList L;
     int i = ;
     for(i=; i<argc; i++){
         if(i>MAXSIZE)
             break;
         L.r[i].key = atoi(argv[i]);
         L.r[i].otherinfo = 'a'+i-;
     }
     L.length = (i-);
     L.r[].key = ;
     L.r[].otherinfo = '';
     printf("输入数据:\n");
     PrintList(L);
     //对顺序表L作树形选择排序
     TreeSelectSort(&L);
     return ;
 }

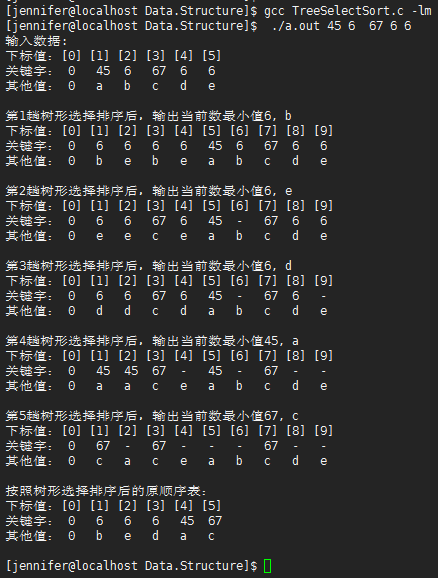
树形选择排序

运行

---

附录1 完全二叉树

定义：设二叉树深度为h，除第h层外，其他各层(1 ~ h-1)的结点数都达到最大个数，第h层所有的结点都集中在最左边，这就是完全二叉树。

性质：

1] 结点i (i>1)的双亲结点为i/2

2] 结点i的左孩子结点为2*i， 右孩子结点为2*i+1

3] 叶子结点数n0, 度为2(有左、右孩子结点)的结点数n2， 则n0 = n2+1

性质3]证明：

　　设n1为二叉树中度为1的结点数。因为二叉树中所有结点数的度均不大于2。所以二叉树的结点数n = n0 + n1 +n2 -- (1)。

　　又除根结点外，其余结点都有一个分支进入，设B为分支总数，则n=B+1。由于这些分支是由度为1或2的结点射出的，所以又有B=n1+2*n2，于是得n = B+1 = n1+2*n2+1 – (2)。

　　由(1)和(2)知， n0 = n2 +1