我见过最棒的证明是文氏图：
（首先要知道二元布尔代数是集合的特殊情况，所以把X和Y当作两个集合，结论成立，那么在二元布尔代数里面也成立。）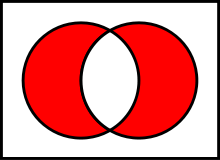

左边的圈是X，右边的圈是Y。
如果是OR 也就是取或，中间的白色的也要填成红色的。
但是，异或 的英文名字叫做exclusive-or ,意思是除掉了（中间部分）的or。

接下来就是玩拼图游戏啦：

X | Y：


x&Y：

X～：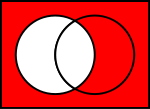

X～ & Y：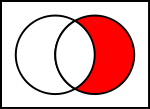

详见：

http://www.zhihu.com/question/20224242

x^y=(x&~y)|(~x&y)证明的更多相关文章

  1. x+y = ((x&y)<<1) + (x^y) 证明

    法一:我们考虑x,y在二进制表示时候,按位相加其中第i位xi+yi = ((xi&yi)<<1) + (xi^yi)其中(xi&yi)<<1表示当xi和yi都是 ...

  2. Codeforces Round #431 (Div. 2) C. From Y to Y

    题目: C. From Y to Y time limit per test 1 second memory limit per test 256 megabytes input standard i ...

  3. 【小知识】比较 x^y 和 y^x 的大小

    往前翻几个编号相邻的题目翻到了这么一道题,感觉很好奇就做了一下 (upd:我下午问了下出题人做法,他就把题隐藏了……这不太友好啊……所以我补一下题意:) 题意 给你两个整数 $x$ 和 $y$,求 $ ...

  4. pageX/Y, offset(), position(), scrollTop(), screenX/Y, clientX/Y, pageX/Y

    event.pageX get mouse position Description: The mouse position relative to the left edge of the docu ...

  5. (x&y) + ((x^y)>>1)即x和y的算数平均值

    (x&y) + ((x^y)>>1)相当于(x+y)/2 (x&y)+((x^y)>>1),把x和y里对应的每一位(指二进制位)都分成三类,每一类分别计算平均值 ...

  6. 原生js获取鼠标坐标方法全面讲解：clientX/Y,pageX/Y,offsetX/Y,layerX/Y,screenX/Y【转】

    关于js鼠标事件综合各大浏览器能获取到坐标的属性总共以下五种 event.clientX/Y event.pageX/Y event.offsetX/Y event.layerX/Y event.sc ...

  7. 给定表达式[x/2] + y + x * y, 其中x,y都是正整数。

    改进了一下,不过还是要十多秒吧. package com.boco.study; import java.math.BigDecimal; import java.util.Calendar; imp ...

  8. clientX/Y,pageX/Y,offsetX/Y,layerX/Y,screenX/Y ,offsetTop,offsetLeft 详解

    clientX/Y: clientX/Y获取到的是触发点相对浏览器可视区域左上角距离,不随页面滚动而改变 兼容性:所有浏览器均支持 pageX/Y: pageX/Y获取到的是触发点相对文档区域左上角距 ...

  9. 关于(x&y)+((x^y)>>1)的探究

    今天在程序员面试宝典上看到 int f(int x int y ) { return (x&y)+((x^y)>>1) } f(729,271) 结果为500 从式子中可以看出分为 ...

  10. 不可表示的数[x/2] + y + x * y

    前端是时间在庞果网上看到不可表示的数的编程题(如下),我自己也试着解答了一下,写的算法虽然没有没有错,但是跑了一些还只是跑到a8,后来到自己整理一下网上的解答过程,虽然解答写的很清晰,但是有些知识还是 ...

随机推荐

  1. zoj Gao The Sequence

    Gao The Sequence Time Limit: 2 Seconds      Memory Limit: 65536 KB You are given a sequence of integ ...

  2. 2016-2017 CT S03E05: Codeforces Trainings Season 3 Episode 5 (2016 Stanford Local Programming Contest, Extended) B

    链接:http://codeforces.com/gym/101116 学弟做的,以后再补 #include <iostream> #include <stdio.h> #in ...

  3. Annotation实战【自定义AbstractProcessor】

    前言 在使用Java的过程中,每个开发人员都接触过@Override, @Deprecated等等各式各样的注解,这些东西是java最基础的一些原生定义好的annotation.本文通过一个实例演示如 ...

  4. WinFormd多窗体 菜单和工具栏：

    一.多窗体 1.哪个是主窗体 主窗体就是如果关掉这个窗体,程序就会退出的那个窗体1问题:主窗体隐藏了,关闭其它窗体后,没有将主窗体显示/关闭,那么程序就关不上了 办法:构造函数传值,将窗体传到另一个窗 ...

  5. Twitter数据抓取

    说明:这里分三个系列介绍Twitter数据的非API抓取方法.有兴趣的QQ群交流: BitCrawler网络爬虫QQ群 322937592 1.Twitter数据抓取(一) 2.Twitter数据抓取 ...

  6. Android 内存溢出解决方案（OOM） 整理总结

    在最近做的工程中发现加载的图片太多或图片过大时经常出现OOM问题,找网上资料也提供了很多方法,但自己感觉有点乱,特此,今天在不同型号的三款安卓手机上做了测试,因为有效果也有结果,今天小马就做个详细的总 ...

  7. CodeForces 12C Fruits

    Fruits Time Limit:1000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u Submit Stat ...

  8. Trigger Execution Sequence Of Oracle Forms

    Sequence of triggers fires on Commit.1.  KEY Commit2.  Pre Commit3.  Pre/On/Post Delete4.  Pre/On/Po ...

  9. 读取视屏文件，保存帧图片为ppm文件

    ffmpeg跟sdl的学习过程:一.版本信息:ffmpeg-3.0.2.tar.bz2SDL2-2.0.4.tar.gz二.编译过程:1.ffmgeg的编译:./configure --enable- ...

  10. 字段符号FIELD-SYMBOLS

    声明:原创作品,转载时请注明文章来自SAP师太技术博客( 博/客/园www.cnblogs.com):www.cnblogs.com/jiangzhengjun,并以超链接形式标明文章原始出处,否则将 ...