HDU 5430 Reflect（欧拉函数）

题目： http://acm.hdu.edu.cn/showproblem.php?pid=5430

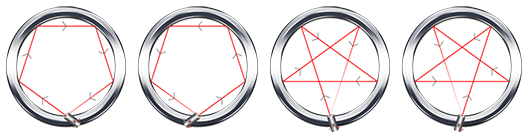
从镜面材质的圆上一点发出一道光线反射NNN次后首次回到起点。
问本质不同的发射的方案数。

输入描述

第一行一个整数T，表示数据组数。T≤10T \leq 10T≤10
对于每一个组，共一行，包含一个整数，表示正整数N(1≤N≤106)N(1 \leq N \leq 10^{6})N(1≤N≤10​6​​)。

输出描述

对于每一个组，输出共一行，包含一个整数，表示答案。

输入样例

1
4

输出样例

4

题解： 

PS： 顺便说一下， 发射角是（0， pi）所以 所求的k在1至N+1 而且 如果不是最简分数（既约分数），

会出现重复计算同一个发射角的情况。

吐槽： 卧槽！ 其实题解中的知识点，小恪也都想到啦！ 无奈没有没有列等式进行化简， 而且我用的是角度值，而不是表示成弧度值 ！ 这道题如果能看出是欧拉函数， 题就水啦！

如果看不出， 那么就和小恪一样， 一起继续努力吧！ Or2        。

#include<iostream>
#include<cstdio>
using namespace std;

int eular(int n)
{
    int ret = , i;
    for (i = ; i*i<=n; i++)
    if(n%i==)
    {
        n/=i, ret*=i-;
        while(n%i==)
        n/=i, ret*=i;
    }
    if(n>) ret*=n-;
    return ret;
} 

int main()
{
    int T, n;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d", &n);
        if(n==) puts("");
        else
        printf("%d\n", eular(n+));
    }
    return ;
}