Poj(3522)，UVa(1395)，枚举生成树

题目链接：http://poj.org/problem?id=3522

Slim Span

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 7522		Accepted: 3988

Description

Given an undirected weighted graph G, you should find one of spanning trees specified as follows.

The graph G is an ordered pair (V, E), where V is a set of vertices {v₁, v₂, …, v_n} and E is a set of undirected edges {e₁, e₂, …, e_m}. Each edge e ∈ E has its weight w(e).

A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n − 1 edges. The slimness of a spanning tree T is defined as the difference between the largest weight and the smallest weight among the n − 1 edges of T.

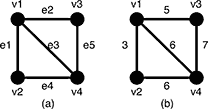
Figure 5: A graph G and the weights of the edges

For example, a graph G in Figure 5(a) has four vertices {v₁, v₂, v₃, v₄} and five undirected edges {e₁, e₂, e₃, e₄, e₅}. The weights of the edges are w(e₁) = 3, w(e₂) = 5, w(e₃) = 6, w(e₄) = 6, w(e₅) = 7 as shown in Figure 5(b).

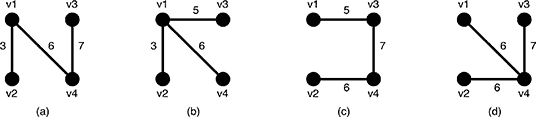
Figure 6: Examples of the spanning trees of G

There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning tree T_a
in Figure 6(a) has three edges whose weights are 3, 6 and 7. The
largest weight is 7 and the smallest weight is 3 so that the slimness of
the tree T_a is 4. The slimnesses of spanning trees T_b, T_c and T_d
shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can
easily see the slimness of any other spanning tree is greater than or
equal to 1, thus the spanning tree Td in Figure 6(d) is one of the
slimmest spanning trees whose slimness is 1.

Your job is to write a program that computes the smallest slimness.

Input

The
input consists of multiple datasets, followed by a line containing two
zeros separated by a space. Each dataset has the following format.

n	m
a1	b1	w1
	⋮
am	bm	wm

Every
input item in a dataset is a non-negative integer. Items in a line are
separated by a space. n is the number of the vertices and m the number
of the edges. You can assume 2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2. a_k and b_k (k = 1, …, m) are positive integers less than or equal to n, which represent the two vertices v_ak and v_bk connected by the kth edge e_k. w_k is a positive integer less than or equal to 10000, which indicates the weight of e_k. You can assume that the graph G = (V, E)
is simple, that is, there are no self-loops (that connect the same
vertex) nor parallel edges (that are two or more edges whose both ends
are the same two vertices).

Output

For
each dataset, if the graph has spanning trees, the smallest slimness
among them should be printed. Otherwise, −1 should be printed. An output
should not contain extra characters.

Sample Input

4 5
1 2 3
1 3 5
1 4 6
2 4 6
3 4 7
4 6
1 2 10
1 3 100
1 4 90
2 3 20
2 4 80
3 4 40
2 1
1 2 1
3 0
3 1
1 2 1
3 3
1 2 2
2 3 5
1 3 6
5 10
1 2 110
1 3 120
1 4 130
1 5 120
2 3 110
2 4 120
2 5 130
3 4 120
3 5 110
4 5 120
5 10
1 2 9384
1 3 887
1 4 2778
1 5 6916
2 3 7794
2 4 8336
2 5 5387
3 4 493
3 5 6650
4 5 1422
5 8
1 2 1
2 3 100
3 4 100
4 5 100
1 5 50
2 5 50
3 5 50
4 1 150
0 0

Sample Output

1
20
0
-1
-1
1
0
1686
50

Source

Japan 2007

 

题意：求最大边与最小边差值最小的生成树

分析：枚举啊！！！

 

#include <stdio.h>
#include <algorithm>

using namespace std;

#define MAXN 6000
#define INF 0x3f3f3f3f

struct Edge
{
    int u,v;
    int w;
} edge[MAXN];

int father[MAXN];

int Find_Set (int x)
{
    if(x!=father[x])
        father[x] = Find_Set(father[x]);
    return father[x];
}

int n,m;
bool cmp(Edge a,Edge b)
{
    return a.w<b.w;
}

int main()
{
    //freopen("input.txt","r",stdin);
    while(scanf("%d%d",&n,&m),n)
    {
        bool flag = false;

        for(int i=; i<m; i++)
            scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].w);
        sort(edge,edge+m,cmp);
        //for(int i=0; i<m; i++)
            //printf("%d ",edge[i].w);
       // puts("");

        int ans = INF;
        int i,j;
        for(i=; i<m; i++)
        {
            for(int i=; i<=n; i++)
                father[i] = i;
            int cnt = ;
            for(j=i; j<m; j++)
            {
                int fx = Find_Set(edge[j].u);
                int fy = Find_Set(edge[j].v);
                if(fx==fy)
                    continue;

                father[fy] = fx;
                cnt++;
                if(cnt==n-)
                {
                    flag = true;
                    break;
                }
            }
            if(cnt==n-)
                ans = min(ans,edge[j].w-edge[i].w);
        }
        if(flag)
            printf("%d\n",ans);
        else puts("-1");
    }
    return ;
}