LCA（最近公共祖先）离线算法Tarjan+并查集

本文来自：http://www.cnblogs.com/Findxiaoxun/p/3428516.html

写得很好，一看就懂了。

在这里就复制了一份。

LCA问题:

给出一棵有根树T，对于任意两个结点u,v求出LCA(T, u, v)，即离根最远的结点x，使得x同时是u和v的祖先。

把LCA问题看成询问式的:给出一系列询问，程序应当对每一个询问尽快做出反应。

对于这类问题有两种解决方法;一是用比较长的时间做预处理，但是等信息充足以后每次回答询问只需要用比较少的时间。这样的算法叫做在线算法。

另外有一类算法是先把所有的询问读入，然后一起把所有询问回答完成，这样的算法叫做离线算法。它们解决的问题都是询问式的，但是方法和特点不同，而且适用范围也不同(如果询问给出是有间隔的，往往只能用在线算法)。希望读者通过LCA问题能够对两类算法的基本设计方法有一个粗略的了解。

最简单的在线算法是先对所有可能的O(n2)种询问计算出结果，然后每次询问都可以在O(1)的时间内直接得到结果。

可以把它转化为O(n2)次单个的 LCA计算(实际上它已经是和离线算法一样了)。

每次可以用如下方法:

单个LCA问题的朴素算法:从u的父亲开始顺着树往上枚举u的祖先并保存在一个列表L中，然后再用类似的方法枚举v，当第一次发现某个祖先x在L中，则输出x.

由于L可以达到O(n)的，所以朴素算法的时间复杂度下限为O(n)。用此法的在线算法的时间复杂度下限为Ω(n3)算法可以通过递推来改进。

在线LCA问题的算法:令L(u)为u的深度(离根的距离)。不妨设L(u)<=L(v)，则如果u是v的父亲,LCA(u,v)=u;否则LCA(u,v) = LCA(u, father(v)).

这样递推的总时间复杂度为O(n2)即在O(n2)的预处理，O(1)的询问时间解决了LCA问题。如果一个在线算法的预处理时间复杂度为O(f(n))，询问时间为O(g(n))，则用O(f(n))-O(g(n))来表示它。

刚才的递推方法给了我们一个启发。当L(u)<=L(v)时，可以根据LCA(u,v)的答案把所有结点分成若干个等价类

1.u的子树上结点v，都满足LCA(u, v)=u;

2.u父亲father(u)的任何不以u为根的子树上结点v都满足LCA(u, v) = father(u);

3.father(father(u))的任何不以father(u)为根的子树上结点v都满足LCA(u,v)=father(father(u))...

这个思路给我们提供了一个不错的离线算法。！！！

请仔细阅读分类这一部分，以上的内容都是lrj的黑书上的，如果看完文章后，仍疑惑，请再次阅读此段！！！

LCA的离线算法

个人认为，之所以离线算法比在线算法时间效率高，主要就是因为离线算法是先存储了查询，然后相当于将查询以一种有序的方式做了安排，而且，是边处理边查询，大大节省了时间。

利用递归的LCA过程。当lca(u)执行完毕后，以u为根的子树已经全部并为了一个集合。而一个lca的内部实际上做了的事就是对其子结点，依 此调用lca。当v1(第一个子结点)被lca，正在处理v2的时候，以v1为根的子树＋u同在一个集合里，f(u)+编号比u小的u的兄弟的子树 同在 一个集合里，f(f(u)) + 编号比f(u)小的 f(u)的兄弟 的子树 同在一个集合里…… 而这些集合，对于v2的LCA都是不同的。因此只要 查询x在哪一个集合里，就能知道LCA(v2,x)

还有一种可能，x不在任何集合里。当他是v2的儿子，v3,v4等子树或编号比u大的u的兄弟的子树（等等）时，就会发生这种情况。即还没有被处理。还没有处理过的怎么办？把一个查询(x1,x2)往查询列表里添加两次，一次添加到x1的列表里，一次添加到x2的列表里，如果在做x1的时候发现 x2已经被处理了，那就接受这个询问。（两次中必定只有一次询问被接受）

void LCA(u){
    for(u的每个儿子v){
        LCA(v);
        union(u,v);
    }
    visit[u]=;
    for(查询中u的每个儿子v){
        if(visit[v])
            u,v的最近公共祖先是father[getfather[v]];
    }
}

这里的union就是并查集中常用的union，即把v并到u的集合里，代表元是u。visit是标记数组，1表示之前已经访问过这个节点了，即，这个点的子树都已经被LCA了。father数组即是并查集的father数组，

getfather是含路径压缩的。

接下来以一个实例来解释这个算法:

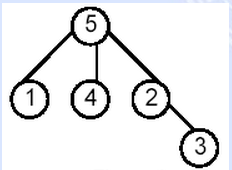
求下面每对点的最近公共祖先

(1 5) (1 4) (4 2) (2 3) (1 3) (4 3)

这是一个普通的二叉树，我们先通过记录入度找到入度为0的节点找到root。然后LCA(root):

root = 5;

对于5的每个儿子，LCA，先LCA(1)，1没有儿子，跳过第一个for，然后，visit[1]=true;查询的vector中(用vector来记录这个树和查询比较好，空间效率比较高)，有一组(1,5)，可是visit[5]现在仍然是初始值false；

然后，退出1的LCA，回到5的LCA，此时，进行5的第二个儿子4，4没有儿子，跳过第一个for，然后visit[4]=true;查询中有三组与4有关的，而只有1被访问过了，那么，ancestor(1,4)=father[getfather[1]]=5

退出4的LCA，回到5的，进行5的第三个儿子2,2有一个儿子，进入3的LCA；

3没有儿子，visit[3]=true;然后有三组查询与3有关，其中，1,4都访问过了，注意，2还没有访问，因为我们进入了LCA(2)的第一个for循环，而且，1,4此时的祖先都是5，那么，ancestor(3,1)=5;ancestor(3,4)=5;注意，此时，3的祖先仍是初始的他自己，如果1还有儿子，而查询的是1的儿子和3的话，1的儿子会被路径压缩，其祖先变成1的祖先5；

退出3的LCA，回到2的，而且把3union到2上了，visit[2]=true；查询中有两组记录与2有关，而且都已经访问过了，那么，也很同之前一样，得出结果。

退出2的LCA，visit[5]=true;还有一个关于5的查询，不再赘述。

程序结束。