HDUOJ----2571（命运）（简单动态规划）

命运

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 8600    Accepted Submission(s): 3032

Problem Description

穿过幽谷意味着离大魔王lemon已经无限接近了！ 可谁能想到，yifenfei在斩杀了一些虾兵蟹将后，却再次面临命运大迷宫的考验，这是魔王lemon设下的又一个机关。要知道，不论何人，若在迷宫中被困1小时以上，则必死无疑！ 可怜的yifenfei为了去救MM，义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧！ 命运大迷宫可以看成是一个两维的方格阵列，如下图所示：

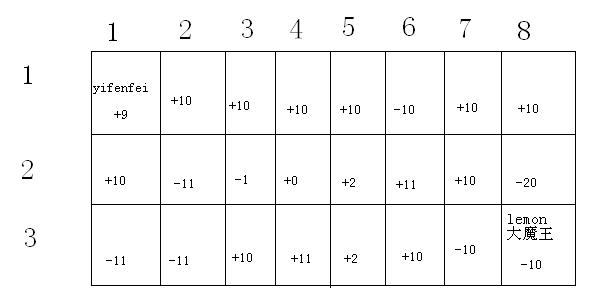
yifenfei一开始在左上角，目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒，所以每个格子都对应一个值，走到那里便自动得到了对应的值。 现在规定yifenfei只能向右或者向下走，向下一次只能走一格。但是如果向右走，则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子，即：如果当前格子是（x,y），下一步可以是（x+1,y），(x,y+1)或者(x,y*k) 其中k>1。 为了能够最大把握的消灭魔王lemon，yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。

 

Input

输入数据首先是一个整数C，表示测试数据的组数。 每组测试数据的第一行是两个整数n,m，分别表示行数和列数(1<=n<=20,10<=m<=1000)； 接着是n行数据，每行包含m个整数，表示n行m列的格子对应的幸运值K ( |k|<100 )。

 

Output

请对应每组测试数据输出一个整数，表示yifenfei可以得到的最大幸运值。

 

Sample Input

1

3 8

9 10 10 10 10 -10 10 10

10 -11 -1 0 2 11 10 -20

-11 -11 10 11 2 10 -10 -10

 

Sample Output

52

 

Author

yifenfei

 

Source

ACM程序设计期末考试081230

代码：

  题目比较的那个，动态规划的题目，两次的规划，首先是向上还是向右，然后是向右多少......!

   提炼两个式子就可以了....

    sum[i][j]=max{ sum[i-1][j] , sum[i][j-1]}+dp[i][j];

    sum[i][j]=max{sum[i][j] , sum[i][k]+dp[i][j]};

代码：

 #include<stdio.h>
 #include<string.h>
 #include<stdlib.h>
 #define maxn -0x3f3f3f3f
 int dp[][],sum[][];
 int max(int a ,int b){
  if(a>b) return a;
          return b;
 }
 int main()
 {
     int c,n,m,k,i,j;
     scanf("%d",&c);
     while(c--){
      scanf("%d%d",&n,&m);
       for(i=; i<=n;i++){
         for(j=;j<=m;j++){
           scanf("%d",&dp[i][j]);
         }
       }
        // memset(sum,0,sizeof(sum));
         //对边缘进行必要地初始化....
         for(i=;i<=n;i++)   sum[i][]=maxn;
         for(i=;i<=m;i++)   sum[][i]=maxn;
         sum[][]=sum[][]=;
         for( i= ; i<=n ; i++ ){
           for( j= ; j<=m ; j++ ){
              //选择是向下还是向右进行行走.......
              sum[i][j]= max( sum[i-][j],sum[i][j-] )+ dp[i][j];
              //对于向右行走，该怎么走.......
              int ks=;
            while(j>=ks){
             if(j%ks==)   //比较它们的倍数
                sum[i][j] = max( sum[i][j] , sum[i][j/ks]+dp[i][j] ) ;
                 ks++;     //所有的倍数.....
             }
           }
         }
         printf("%d\n",sum[n][m]);
     }
     return ;
 }