WPF将点列连接成光滑曲线——贝塞尔曲线

原文:WPF将点列连接成光滑曲线——贝塞尔曲线

背景

最近在写一个游戏场景编辑器，虽然很水，但是还是遇到了不少问题。连接离散个点列成为光滑曲线就是一个问题。主要是为了通过关键点产生2D的赛道场景。总之马路不可能是直线相连的，当然需要曲线光滑相连。现在我就来解决这个问题。

贝塞尔曲线

贝塞尔曲线，又称贝兹曲线或贝济埃曲线，一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。当然在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。在Flash4中还没有完整的曲线工具，而在Flash5里面已经提供出贝塞尔曲线工具。

这里是百度里面的介绍。直接搬过来了。

问题

如图，这些绿色的点我们希望用光滑的曲线连接它们。

看看WPF给我们提供的函数：

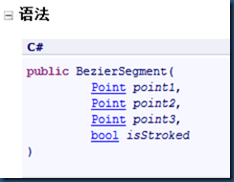
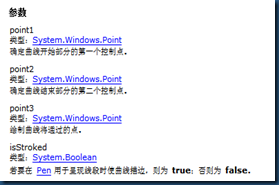
来自MSDN

我们发现point3和point4是我们需要的，这两个点我们直接可以从点列中取得，但是point1和point2如何获取呢？控制点到底是个什么东西。当然我试了很多次失败了很多次~~

巧妙的解决方案

大致思路就是 先算出相邻原始点的中点，在把相邻中点连成的线段平移到对应的原始点，以平移后的中点作为控制点，相邻原始点为起始点画贝塞尔曲线，这样就保证了连接处的光滑。而贝塞尔曲线本身是光滑的，所以就把这些原始点用光滑曲线连起来了。

（http://liyiwen.javaeye.com/blog/705489）

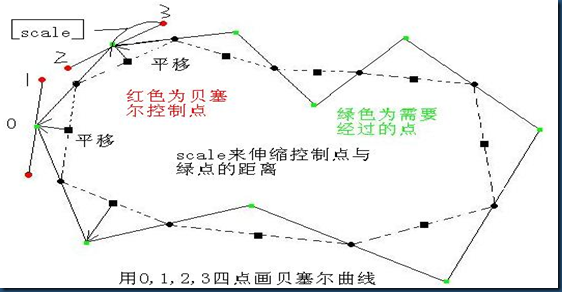
实验结果

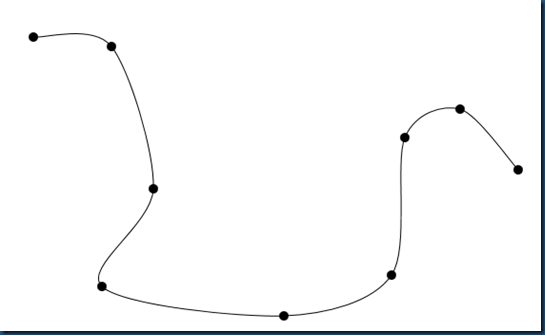
看起来连接的还是比较光滑的。

相关代码

Path path;
        public void UpdateRoad()
        {
            MapCanvas.Children.Remove(path);
            if (ScenePoint.roadPoint.Count > 0)
            {
                List<Point> list = new List<Point>();
                foreach (ScenePoint sp in ScenePoint.roadPoint)
                {
                    list.Add(new Point((sp.position.X + Shift.X) * Zoom, (sp.position.Y + Shift.Y) * Zoom));
                }
                PathFigure pf = new PathFigure();

                pf.StartPoint = list[0];
                List<Point> controls = new List<Point>();
                for (int i = 0; i < list.Count; i++)
                {
                    controls.AddRange(Control1(list, i));
                }
                for (int i = 1; i < list.Count; i++)
                {
                    BezierSegment bs = new BezierSegment(controls[i * 2 - 1], controls[i * 2], list[i], true);
                    bs.IsSmoothJoin = true;

                    pf.Segments.Add(bs);
                }
                PathFigureCollection pfc = new PathFigureCollection();
                pfc.Add(pf);
                PathGeometry pg = new PathGeometry(pfc);

                path = new Path();
                path.Stroke = Brushes.Black;
                path.Data = pg;
                MapCanvas.Children.Add(path);
            }
        }
        public void UpdateHeightCanvas()
        {
            HeightCanvas.Children.Clear();
            foreach (ScenePoint sp in ScenePoint.listPoint)
            {
                HeightCanvas.Children.Add(sp.Ellipseh);
            }
        }
        public List<Point> Control1(List<Point> list, int n)
        {
            List<Point> point = new List<Point>();
            point.Add(new Point());
            point.Add(new Point());
            if (n == 0)
            {
                point[0] = list[0];
            }
            else
            {
                point[0] = Average(list[n - 1], list[n]);
            }
            if (n == list.Count - 1)
            {
                point[1] = list[list.Count - 1];
            }
            else
            {
                point[1] = Average(list[n], list[n+1]);
            }
            Point ave = Average(point[0], point[1]);
            Point sh = Sub(list[n], ave);
            point[0] = Mul(Add(point[0], sh),list[n],0.6);
            point[1] = Mul(Add(point[1], sh),list[n],0.6);
            //Line line = new Line();
            //line.X1 = point[0].X;
            //line.Y1 = point[0].Y;
            //line.X2 = point[1].X;
            //line.Y2 = point[1].Y;
            //line.Stroke = Brushes.Red;
            //MapCanvas.Children.Add(line);
            return point;
        }
        public Point Average(Point x, Point y)
        {
            return new Point((x.X+y.X)/2,(x.Y+y.Y)/2);
        }
        public Point Add(Point x, Point y)
        {
            return new Point(x.X + y.X, x.Y + y.Y);
        }
        public Point Sub(Point x, Point y)
        {
            return new Point(x.X - y.X, x.Y - y.Y);
        }
        public Point Mul(Point x, Point y,double d)
        {
            Point temp = Sub(x, y);
            temp = new Point(temp.X * d, temp.Y * d);
            temp = Add(y, temp);
            return temp;
        }