codeforce 571 B Minimization

题意：给出一个序列，经过合适的排序后。使得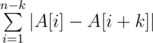最小。

做法：将a升序排序后，dp[i][j]:选择i个数量为n/k的集合，选择j个数量为n/k+1的集合的最小值。

举个样例，

a={1,2,3,4,5,6,7,8,9,10},k=2

那么直接贪心可做，是这样。

1,x,2,x,3,x,4,x,5,x。(也就是1,2,3,4,5作为一个集合)

6    7   8    9    10(也就是6,7,8,9,10作为一个集合)

放在一起就是1，6。2。7。3，8，4。9，5，10。

若是k=3就要考虑长度为n/k+1=4的集合，是将1,2,3,4放在一起呢？还是4。5。6，7放在一起呢？就须要dp了。

dp[i+1][j]=min(dp[i+1][j],dp[i][j]+sb[x+sz-1]-sb[x]);

dp[i][j+1]=min(dp[i][j+1],dp[i][j]+sb[x+sz]-sb[x]);

x:当前还未考虑元素的最小下标

sb:一段连续元素差的和

#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<iostream>
#include<algorithm>
#include<bitset>
#include<climits>
#include<list>
#include<iomanip>
#include<stack>
#include<set>
using namespace std;
typedef long long ll;
int a[300010];
ll sb[3000010];
ll dp[5010][5010];
int main()
{
	int n,k;
	cin>>n>>k;
	int sz=n/k;
	for(int i=0;i<n;i++)
		cin>>a[i];
	sort(a,a+n);
	for(int i=1;i<n;i++)
		sb[i]=sb[i-1]+a[i]-a[i-1];
	memset(dp,63,sizeof(dp));
	dp[0][0]=0;
	int m=n%k,len=k-m;
	for(int i=0;i<=len;i++)
		for(int j=0;j<=m;j++)
		{
			int x=(i+j)*sz+j;
			dp[i+1][j]=min(dp[i+1][j],dp[i][j]+sb[x+sz-1]-sb[x]);
			dp[i][j+1]=min(dp[i][j+1],dp[i][j]+sb[x+sz]-sb[x]);
		}
	cout<<dp[len][m];
}

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You've got array A, consisting of n integers
and a positive integer k. Array A is
indexed by integers from 1 to n.

You need to permute the array elements so that value

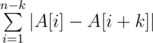
became minimal possible. In particular, it is allowed not to change order of elements at all.

Input

The first line contains two integers n, k (2 ≤ n ≤ 3·105, 1 ≤ k ≤ min(5000, n - 1)).

The second line contains n integers A[1], A[2], ..., A[n] ( - 109 ≤ A[i] ≤ 109),
separate by spaces — elements of the array A.

Output

Print the minimum possible value of the sum described in the statement.

Sample test(s)

input

3 2
1 2 4

output

1

input

5 2
3 -5 3 -5 3

output

0

input

6 3
4 3 4 3 2 5

output

3

Note

In the first test one of the optimal permutations is 1 4 2.

In the second test the initial order is optimal.

In the third test one of the optimal permutations is 2 3 4 4 3 5.