洛谷P4012 深海机器人问题(费用流)

题目描述

深海资源考察探险队的潜艇将到达深海的海底进行科学考察。

潜艇内有多个深海机器人。潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。

深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。

每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。

本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。

用一个 P\times QP×Q 网格表示深海机器人的可移动位置。西南角的坐标为 (0,0)(0,0) ，东北角的坐标为 (Q,P)(Q,P) 。

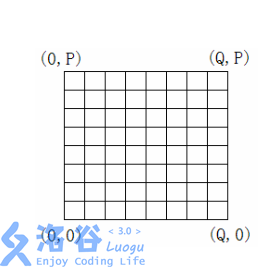
给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。

计算深海机器人的最优移动方案，使深海机器人到达目的地后，采集到的生物标本的总价值最高。

输入输出格式

输入格式：

文件的第 11 行为深海机器人的出发位置数 aa ,和目的地数 bb 。

第 22 行为 PP 和 QQ 的值。

接下来的 P+1P+1 行,每行有 QQ 个正整数,表示向东移动路径上生物标本的价值,行数据依从南到北方向排列。

再接下来的 Q+1Q+1 行,每行有 PP 个正整数,表示向北移动路径上生物标本的价值,行数据依从西到东方向排列。

接下来的 aa 行,每行有 33 个正整数 k,x,yk,x,y ,表示有 kk 个深海机器人从 (x,y)(x,y) 位置坐标出发。

再接下来的 bb 行,每行有 33 个正整数 r,x,yr,x,y ,表示有 rr 个深海机器人可选择 (x,y)(x,y) 位置坐标作为目的地。

a行和b行输入时横纵坐标要反过来

输出格式：

输出采集到的生物标本的最高总价值.

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

1\leq P,Q\leq151≤P,Q≤15

1\leq a\leq 41≤a≤4

1\leq b\leq 61≤b≤6

费用流应该比较显然

就是读入比较坑爹

需要把整张图反过来

从S向每个机器人开始的地方连容量为机器人数量，费用为0的边

从每个机器人向T连容量为数量，费用为0的边

相邻格子之间连一条容量为INF，费用为0的边，再连一条容量为1，费用为读入的边

#include<cstdio>

#include<cstring>

#include<queue>

#include<algorithm>

#define AddEdge(x,y,z,f) add_edge(x,y,z,f),add_edge(y,x,-z,0)

using namespace std;

const int INF=1e8+;

const int MAXN=+;

int N,M,S,T;

int C[MAXN][MAXN];

struct node

{

    int u,v,w,f,nxt;

}edge[MAXN];

int head[MAXN],num=;

inline void add_edge(int x,int y,int z,int f)

{

    edge[num].u=x;

    edge[num].v=y;

    edge[num].w=z;

    edge[num].f=f;

    edge[num].nxt=head[x];

    head[x]=num++;

}

int dis[MAXN],vis[MAXN],Pre[MAXN];

bool SPFA()

{

    memset(dis,0xf,sizeof(dis));

    memset(vis,,sizeof(vis));

    queue<int>q;

    q.push(S);

    dis[S]=;

    while(q.size()!=)

    {

        int p=q.front();q.pop();

        vis[p]=;

        for(int i=head[p];i!=-;i=edge[i].nxt)

        {

            if(edge[i].f&&dis[edge[i].v]>dis[p]+edge[i].w)

            {

                dis[edge[i].v]=dis[p]+edge[i].w;

                Pre[edge[i].v]=i;

                if(!vis[edge[i].v])

                    vis[edge[i].v]=,q.push(edge[i].v);

            }

        }

    }

    return dis[T]<INF;

}

int F()

{

    int nowflow=INF;

    for(int now=T;now!=S;now=edge[Pre[now]].u)

        nowflow=min(nowflow,edge[Pre[now]].f);

    for(int now=T;now!=S;now=edge[Pre[now]].u)

        edge[Pre[now]].f-=nowflow,

        edge[Pre[now]^].f+=nowflow;

    return nowflow*dis[T];

}

void MCMF()

{

    int ans=;

    while(SPFA())

        ans+=F();

    printf("%d\n",abs(ans));

}

int belong[MAXN][MAXN];

int main()

{

    #ifdef WIN32

    freopen("a.in","r",stdin);

    #endif

    memset(head,-,sizeof(head));

    int a,b,P,Q;

    scanf("%d%d",&a,&b);

    scanf("%d%d",&P,&Q);

    P++;Q++;

    S=,T=;

    for(int i=;i<=P;i++)

        for(int j=;j<=Q;j++)

            belong[i][j]=(i-)*Q+j;

    for(int i=;i<=P;i++)

    {

        for(int j=;j<=Q-;j++)

        {

            int x;

            scanf("%d",&x);

            AddEdge(belong[i][j],belong[i][j+],-x,);

            AddEdge(belong[i][j],belong[i][j+],,INF);

        }

    }

    for(int j=;j<=Q;j++)

    {

        for(int i=;i<=P-;i++)

        {

            int x;

            scanf("%d",&x);

            AddEdge(belong[i][j],belong[i+][j],-x,);

            AddEdge(belong[i][j],belong[i+][j],,INF);

        }

    }

    for(int i=;i<=a;i++)

    {

        int num,x,y;

        scanf("%d%d%d",&num,&x,&y);

        AddEdge(S,belong[x+][y+],,num);

    }

    for(int i=;i<=b;i++)

    {

        int num,x,y;

        scanf("%d%d%d",&num,&x,&y);

        AddEdge(belong[x+][y+],T,,num);

    }

    MCMF();

    return ;

}