洛谷P2052 道路修建

P2052 道路修建

题目描述

在 W 星球上有 n 个国家。为了各自国家的经济发展，他们决定在各个国家 之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬，他们只愿 意修建恰好 n – 1 条双向道路。 每条道路的修建都要付出一定的费用，这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如，在下图中，虚线所示道路两端分别有 2 个、4 个国家，如果该道路长度为 1，则费用为 1×|2 – 4|=2。图中圆圈里的数字表示国 家的编号。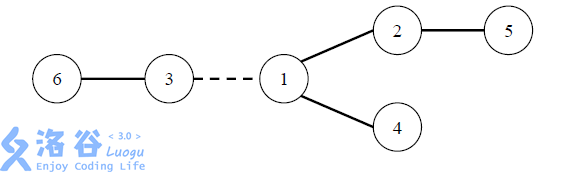 

由于国家的数量十分庞大，道路的建造方案有很多种，同时每种方案的修建 费用难以用人工计算，国王们决定找人设计一个软件，对于给定的建造方案，计 算出所需要的费用。请你帮助国王们设计一个这样的软件。

输入输出格式

输入格式：

输入的第一行包含一个整数 n，表示 W 星球上的国家的数量，国家从 1 到 n 编号。 接下来 n – 1 行描述道路建设情况，其中第 i 行包含三个整数 ai、bi和 ci，表 示第 i 条双向道路修建在 ai与 bi两个国家之间，长度为 ci。

输出格式：

输出一个整数，表示修建所有道路所需要的总费用。

输入输出样例

输入样例#1： 复制

6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1

输出样例#1： 复制

20

说明

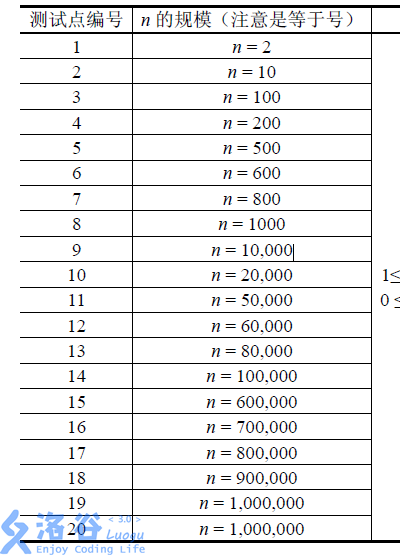
1≤ai, bi≤n

0≤ci≤106

2≤n≤106

/*
    dfs一遍求出每个子树的大小，然后显然……
*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#define maxn 1000010
using namespace std;
int n,num,head[maxn],sz[maxn];
struct node{int to,pre;}e[maxn*];
struct Node{int from,to,v;}E[maxn];
void Insert(int from,int to){
    e[++num].to=to;
    e[num].pre=head[from];
    head[from]=num;
}
void dfs(int now,int father){
    sz[now]=;
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==father)continue;
        dfs(to,now);
        sz[now]+=sz[to];
    }
}
int main(){
    freopen("Cola.txt","r",stdin);
    scanf("%d",&n);
    for(int i=;i<n;i++){
        scanf("%d%d%d",&E[i].from,&E[i].to,&E[i].v);
        Insert(E[i].from,E[i].to);
        Insert(E[i].to,E[i].from);
    }
    dfs(,);
    long long ans=;
    for(int i=;i<n;i++){
        int x=E[i].from,y=E[i].to;
        if(sz[x]<sz[y])swap(x,y);
        int s1=n-sz[y],s2=sz[y];
        ans+=1LL*E[i].v*abs(s1-s2);
    }
    cout<<ans;
}