【BZOJ2006】[NOI2010] 超级钢琴（堆+RMQ）

点此看题面

大致题意： 要你求出区间和前\(k\)大的区间的区间和之和，其中每个区间的大小在\(L\)与\(R\)之间。

堆+\(RMQ\)

这道题目，我们可以先对\(1\sim n\)中的每一个\(i\)假设它为左端点，求出区间\([i+L-1,min(i+R-1,n)]\)中的一个右端点\(s\)，使得对于任意一个\(j∈[i+L-1,min(i+R-1,n)]\)，满足\(\sum_{x=i}^s a[x]>=\sum_{y=i}^j a[y]\)（这可以直接对每个位置的前缀和求\(RMQ\)）。

然后，将每个\([i+L-1,s]\)的区间和扔入一个堆中维护。

进一步思考

一起来观察一下下面这张图：

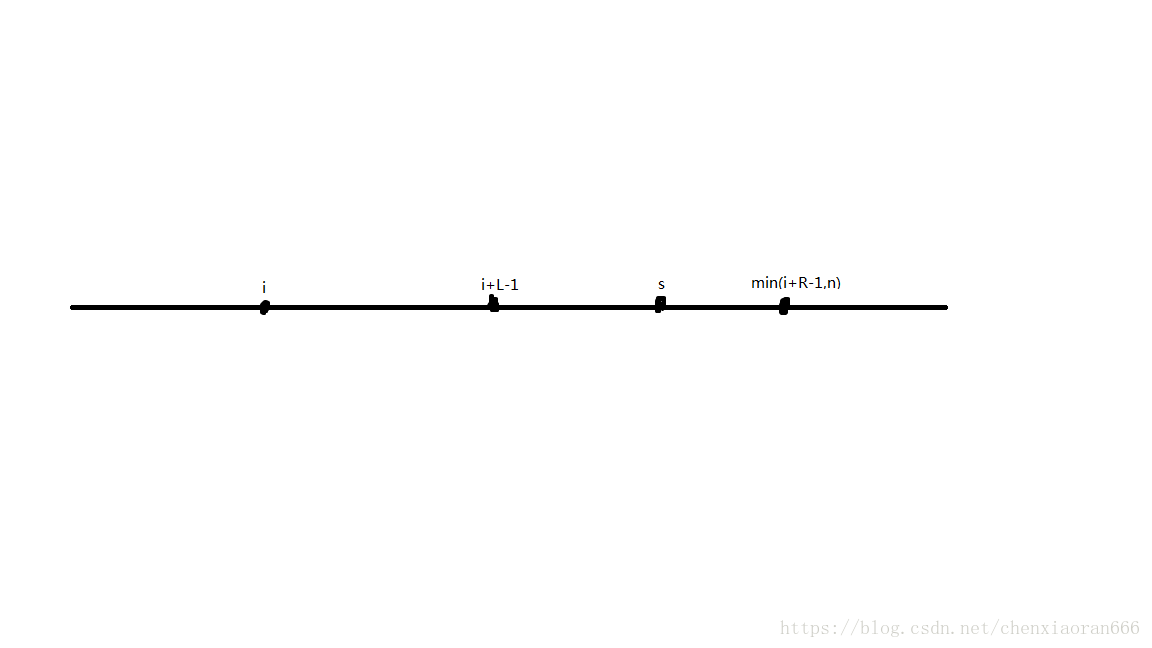
我们会发现，\([i+L-1,s-1]\)和\([s+1,min(i+R-1,n)]\)两个区间中也可能含有使答案区间和前\(k\)大的右端点，所以，对于一个答案，我们在将其统计之后，需要将它重新拆成两部分再分别扔回堆中，这样就能保证没有遗漏了。

代码

#include<bits/stdc++.h>
#define LL long long
#define N 500000
using namespace std;
int n,m,l,r,a[N+5],Log2[N+5];
LL sum[N+5];
struct RMQ//RMQ区间最值
{
    LL Max,Maxer;//Max存储最大的数，Maxer存储最大的数的编号
    bool operator < (const RMQ a) const//比较两个RMQ结构体的大小
    {
        return Max<a.Max;//比较最大的数的大小
    }
}R[N+5][25];
struct key
{
    LL x,y,s,val,pos;//x,y表示区间能选的范围，pos,s表示选择了的区间的范围，val表示这个选择了的区间的区间和
    bool operator < (const key a) const//比较两个key结构体的大小
    {
        return val<a.val;//比较区间和的大小
    }
};
priority_queue<key> h;//一个堆
inline char tc()
{
    static char ff[100000],*A=ff,*B=ff;
    return A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0;int f=1;char ch;
    while(!isdigit(ch=tc())) if(ch=='-') f=-1;
    while(x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
    x*=f;
}
inline void write(LL x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
inline void Start()//预处理
{
    for(register int j=1;j<=25;++j)//预处理出RMQ
        for(register int i=1;i+(1<<(j-1))<=n;++i)
            R[i][j]=max(R[i][j-1],R[i+(1<<(j-1))][j-1]);
    for(register int i=2;i<=n;++i) Log2[i]=Log2[i>>1]+1;//预处理出Log2[]，减少精度误差
}
inline int Maxer(int l,int r)//返回这段区间内能使区间和最大的位置
{
    int k=Log2[r-l+1];//一个RMQ的过程
    return max(R[l][k],R[r-(1<<k)+1][k]).Maxer;
}
int main()
{
    register int i;
    for(read(n),read(m),read(l),read(r),i=1;i<=n;++i) read(a[i]),R[R[i][0].Maxer=i][0].Max=sum[i]=sum[i-1]+a[i];
    Start();
    for(i=1;i<=n-l+1;++i) h.push((key){i+l-1,(i+r-1<n?i+r-1:n),Maxer(i+l-1,(i+r-1<n?i+r-1:n)),sum[Maxer(i+l-1,(i+r-1<n?i+r-1:n))]-sum[i-1],i});//先将每一个区间加入堆
    LL ans=0;//ans统计答案
    while(m--)
    {
        key k=h.top();
        h.pop(),ans+=k.val;//更新ans
        if(k.x!=k.s) h.push((key){k.x,k.s-1,Maxer(k.x,k.s-1),sum[Maxer(k.x,k.s-1)]-sum[k.pos-1],k.pos});//若左边还有区间，就将左边一部分重新扔入堆中
        if(k.s!=k.y) h.push((key){k.s+1,k.y,Maxer(k.s+1,k.y),sum[Maxer(k.s+1,k.y)]-sum[k.pos-1],k.pos});//若右边还有区间，就将右边一部分重新扔入堆中
    }
    return write(ans),0;
}