简析平衡树（一）——替罪羊树 Scapegoat Tree

前言

平衡树在我的心目中，一直都是一个很高深莫测的数据结构。不过，由于最近做的题目的题解中经常出现“平衡树”这三个字，我决定从最简单的替罪羊树开始，好好学习平衡树。

简介

替罪羊树，英文名\(Scapegoat\ Tree\)，是我认为平衡树中最简单的一种。

替罪羊树可以当作一棵非常暴力的二叉搜索树，因为它除了在子树不平衡时会暴力重构（不然为什么叫它平衡树）以外几乎和BST没有任何区别。

替罪羊树的基础操作

• 插入

  不得不说，替罪羊树的插入操作简直与BST一模一样。
  
  直接上代码：

inline void Insert(int &x,int val)//插入操作
{
    if(!x)//如果当前节点为空，那么就将元素插入这个节点
    {
        x=Void[tot--],node[x].Val=val,node[x].Exist=1,Build(x);
        return;
    }
    ++node[x].Size,++node[x].Fac;//将这个子树的大小加1
    if(val<=node[x].Val) Insert(node[x].Son[0],val);//比较插入元素与当前元素，若小于等于当前元素，就插入到当前元素的左子树
    else Insert(node[x].Son[1],val);//否则，就插入到当前元素的右子树
}

• 删除

  替罪羊树的删除操作就很值得一提了。

  在删除替罪羊树上的一个元素时，我们并不会将其暴力删除（虽然替罪羊树在重构时非常暴力，但它的暴力是有选择性的，不然复杂度还不上天），而是标记这个节点不存在，并在计算它所在子树大小时将实际大小减1。这个思想是非常实用的，在许多地方我们都会用到。

  代码如下：

inline void Delete(int &x,int rk)//删除排名为rk的数
{
    if(node[x].Exist&&!((node[node[x].Son[0]].Fac+1)^rk))//如果当前节点存在（没有被删除）且刚好排名为rk，我们就将其删除
    {
        node[x].Exist=0,--node[x].Fac;//标记其不存在，并将该子树的实际大小减1
        return;
    }
    --node[x].Fac;//因为该子树中将有元素被删除，所以将该子树的实际大小减1
    if(node[node[x].Son[0]].Fac+node[x].Exist>=rk) Delete(node[x].Son[0],rk);//比较删除元素与当前元素的大小，若小于等于当前元素，就说明要删除的元素在当前元素的左子树
    else Delete(node[x].Son[1],rk-node[x].Exist-node[node[x].Son[0]].Fac);//否则说明要删除的元素在当前元素的右子树
}
inline void del(int v)//删除值为v的数
{
    Delete(rt,get_rank(v));//删除值为v的数，就相当于删除排名为值为v的数的排名的数，是不是有点绕？
    if((double)node[rt].Size*alpha>(double)node[rt].Fac) ReBuild(rt);//如果当前子树的实际大小小于该子树的大小乘以alpha（一般来说，取alpha=0.75），就重构该子树
}

• 重构

  呃，接下来到了最关键的部分：重构。

  替罪羊树的重构真的是非常暴力。我们可以形象地理解它：

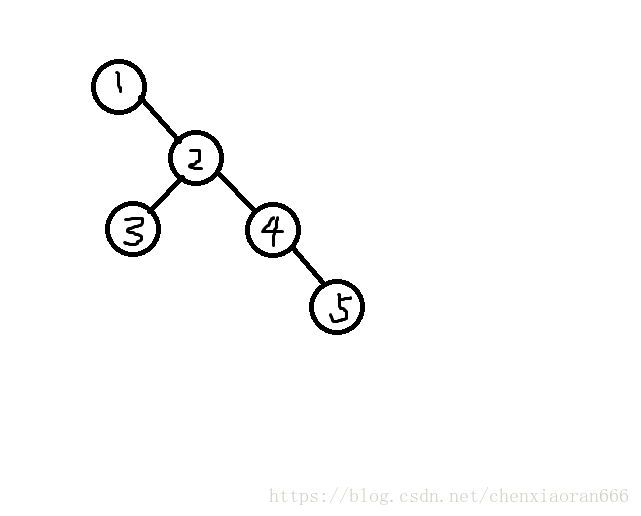
假设上图是一棵需要重构的子树（圆圈中是节点编号而不是节点权值）。

那么，我们就先非常暴力地将其拍扁：

然后，再将它以最中间的节点为新的根，重新拎起来：

重构就完成了。是不是一个极其暴力的过程？

代码如下：

inline void Traversal(int x)//拍扁原子树（中序遍历原子树，这样可以保证遍历后得到的元素是从大到小排序的）
{
    if(!x) return;//如果当前节点是空节点，就退出函数
    Traversal(node[x].Son[0]);//由于是中序遍历，所以先遍历该节点的左子树
    if(node[x].Exist) cur[++cnt]=x;//如果该节点存在，就将其加入数组
    else Void[++tot]=x;//否则删除该节点，将该节点加入存储空节点的数组，方便动态开点
    Traversal(node[x].Son[1]);//最后遍历该节点的右子树
}
inline void SetUp(int l,int r,int &x)//将拍扁的树重新拎起（一个分治的操作）
{
    int mid=l+r>>1;x=cur[mid];//将新的根节点设定为这段区间的中点（使重构出的树尽量平衡）
    if(l==r)//如果这是一个叶子节点
    {
        Build(x);//重置该节点
        return;//退出函数
    }
    if(l<mid) SetUp(l,mid-1,node[x].Son[0]);//如果当前元素左边还有数，说明它有左子树，重构它的左子树
    else node[x].Son[0]=0;//否则它的左子树为空
    SetUp(mid+1,r,node[x].Son[1]),PushUp(x);//重构它的右子树
}
inline void ReBuild(int &x)//重构的过程
{
    cnt=0,Traversal(x);//拍扁
    if(cnt) SetUp(1,cnt,x);//拎起
    else x=0;//特判该子树为空的情况
}

• 询问

  这应该是替罪羊树中最后一个比较基础的操作了。

  作为一棵升级版的BST，它的功能与BST差不多：询问值为\(v\)的数的排名和排名为\(rk\)的数的值。

  查询过程也与BST差不多，只不过要多判断一些节点不存在的情况。

  代码如下：

inline int get_rank(int v)//询问值为v的数的排名
{
    int x=rt,rk=1;//初始化计数器为1（v本身）
    while(x)//只要当前节点不为空
    {
        if(node[x].Val>=v) x=node[x].Son[0];//如果当前元素大于v，则说明当前元素的排名大于v，所以访问当前元素的左子树
        else rk+=node[node[x].Son[0]].Fac+node[x].Exist,x=node[x].Son[1];//否则，将计数器加上当前元素的排名，并访问当前元素的右子树
    }
    return rk;
}

inline int get_val(int rk)//询问排名为rk的数的值
{
    int x=rt;
    while(x)//只要当前节点不为空
    {
        if(node[x].Exist&&node[node[x].Son[0]].Fac+1==rk) return node[x].Val;//如果当前元素的排名等于rk，则返回该节点的值
        else if(node[node[x].Son[0]].Fac>=rk) x=node[x].Son[0];//否则，如果当前元素的排名大于rk，访问当前元素的左子树
        else rk-=node[x].Exist+node[node[x].Son[0]].Fac,x=node[x].Son[1];//不然，就将rk减去当前元素的排名，访问当前元素的右子树
    }
}

完整代码

讲了这么多，最后来一个模板：（以【洛谷3369】【模板】普通平衡树为例）

#include<bits/stdc++.h>
#define N 100000
using namespace std;
int n,st,rt,cnt,tot,cur[N+5],Void[N+5];
const double alpha=0.75;
struct Scapegoat
{
    int Son[2],Exist,Val,Size,Fac;
}node[N+5];
inline char tc()
{
    static char ff[100000],*A=ff,*B=ff;
    return A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0;int f=1;char ch;
    while(!isdigit(ch=tc())) if(ch=='-') f=-1;
    while(x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
    x*=f;
}
inline void write(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
inline void Init()
{
    tot=0;
    for(register int i=N-1;i;--i) Void[++tot]=i;
}
inline bool balance(int x)
{
    return (double)node[x].Fac*alpha>(double)max(node[node[x].Son[0]].Fac,node[node[x].Son[1]].Fac);
}
inline void Build(int x)
{
    node[x].Son[0]=node[x].Son[1]=0,node[x].Size=node[x].Fac=1;
}
inline void Insert(int &x,int val)
{
    if(!x)
    {
        x=Void[tot--],node[x].Val=val,node[x].Exist=1,Build(x);
        return;
    }
    ++node[x].Size,++node[x].Fac;
    if(val<=node[x].Val) Insert(node[x].Son[0],val);
    else Insert(node[x].Son[1],val);
}
inline void PushUp(int x)
{
    node[x].Size=node[node[x].Son[0]].Size+node[node[x].Son[1]].Size+1,node[x].Fac=node[node[x].Son[0]].Fac+node[node[x].Son[1]].Fac+1;
}
inline void Traversal(int x)
{
    if(!x) return;
    Traversal(node[x].Son[0]);
    if(node[x].Exist) cur[++cnt]=x;
    else Void[++tot]=x;
    Traversal(node[x].Son[1]);
}
inline void SetUp(int l,int r,int &x)
{
    int mid=l+r>>1;x=cur[mid];
    if(l==r)
    {
        Build(x);
        return;
    }
    if(l<mid) SetUp(l,mid-1,node[x].Son[0]);
    else node[x].Son[0]=0;
    SetUp(mid+1,r,node[x].Son[1]),PushUp(x);
}
inline void ReBuild(int &x)
{
    cnt=0,Traversal(x);
    if(cnt) SetUp(1,cnt,x);
    else x=0;
}
inline void check(int x,int val)
{
    int s=val<=node[x].Val?0:1;
    while(node[x].Son[s])
    {
        if(!balance(node[x].Son[s]))
        {
            ReBuild(node[x].Son[s]);
            return;
        }
        x=node[x].Son[s],s=val<=node[x].Val?0:1;
    }
}
inline int get_rank(int v)
{
    int x=rt,rk=1;
    while(x)
    {
        if(node[x].Val>=v) x=node[x].Son[0];
        else rk+=node[node[x].Son[0]].Fac+node[x].Exist,x=node[x].Son[1];
    }
    return rk;
}
inline int get_val(int rk)
{
    int x=rt;
    while(x)
    {
        if(node[x].Exist&&node[node[x].Son[0]].Fac+1==rk) return node[x].Val;
        else if(node[node[x].Son[0]].Fac>=rk) x=node[x].Son[0];
        else rk-=node[x].Exist+node[node[x].Son[0]].Fac,x=node[x].Son[1];
    }
}
inline void Delete(int &x,int rk)
{
    if(node[x].Exist&&!((node[node[x].Son[0]].Fac+1)^rk))
    {
        node[x].Exist=0,--node[x].Fac;
        return;
    }
    --node[x].Fac;
    if(node[node[x].Son[0]].Fac+node[x].Exist>=rk) Delete(node[x].Son[0],rk);
    else Delete(node[x].Son[1],rk-node[x].Exist-node[node[x].Son[0]].Fac);
}
inline void del(int v)
{
    Delete(rt,get_rank(v));
    if((double)node[rt].Size*alpha>(double)node[rt].Fac) ReBuild(rt);
}
int main()
{
    for(read(n),Init();n;--n)
    {
        int op,x;read(op),read(x);
        switch(op)
        {
            case 1:st=rt,Insert(rt,x),check(st,x);break;
            case 2:del(x);break;
            case 3:write(get_rank(x)),putchar('\n');break;
            case 4:write(get_val(x)),putchar('\n');break;
            case 5:write(get_val(get_rank(x)-1)),putchar('\n');break;
            case 6:write(get_val(get_rank(x+1))),putchar('\n');break;
        }
    }
    return 0;
}