【BZOJ5020】[THUWC 2017]在美妙的数学王国中畅游 泰勒展开+LCT

【BZOJ5020】[THUWC 2017]在美妙的数学王国中畅游

Description

数字和数学规律主宰着这个世界。

机器的运转，

生命的消长，

宇宙的进程，

这些神秘而又美妙的过程无不可以用数学的语言展现出来。

这印证了一句古老的名言：

“学好数理化，走遍天下都不怕。”

学渣小R被大学的数学课程虐得生活不能自理，微积分的成绩曾是他在教室里上的课的最低分。然而他的某位陈姓室友却能轻松地在数学考试中得到满分。为了提升自己的数学课成绩，有一天晚上（在他睡觉的时候），他来到了数学王国。

数学王国中，每个人的智商可以用一个属于 [0,1]的实数表示。数学王国中有 n 个城市，编号从 0 到 n−1 ，这些城市由若干座魔法桥连接。每个城市的中心都有一个魔法球，每个魔法球中藏有一道数学题。每个人在做完这道数学题之后都会得到一个在 [0,1] 区间内的分数。一道题可以用一个从 [0,1] 映射到 [0,1]的函数 f(x) 表示。若一个人的智商为 x ，则他做完这道数学题之后会得到 f(x)分。函数 f有三种形式：

    正弦函数 sin(ax+b) (a∈[0,1],b∈[0,π],a+b∈[0,π])

    指数函数 e^(ax+b) (a∈[−1,1],b∈[−2,0],a+b∈[−2,0])

    一次函数 ax+b (a∈[−1,1],b∈[0,1],a+b∈[0,1]

数学王国中的魔法桥会发生变化，有时会有一座魔法桥消失，有时会有一座魔法桥出现。但在任意时刻，只存在至多一条连接任意两个城市的简单路径（即所有城市形成一个森林）。在初始情况下，数学王国中不存在任何的魔法桥。

数学王国的国王拉格朗日很乐意传授小R数学知识，但前提是小R要先回答国王的问题。这些问题具有相同的形式，即一个智商为 x 的人从城市 u 旅行到城市 v（即经过 u 到 v 这条路径上的所有城市，包括 u和 v ）且做了所有城市内的数学题后，他所有得分的总和是多少。

Input

第一行两个正整数 n,m 和一个字符串 type 。

表示数学王国中共有 n 座城市，发生了 m 个事件，该数据的类型为 type 。 

typet 字符串是为了能让大家更方便地获得部分分，你可能不需要用到这个输入。

其具体含义在【数据范围与提示】中有解释。

接下来 n 行，第 i 行表示初始情况下编号为 i 的城市的魔法球中的函数。

一个魔法用一个整数 f表示函数的类型，两个实数 a,b 表示函数的参数，若

    f=1,则函数为 f(x)=sin(ax+b)(a∈[0,1],b∈[0,π],a+b∈[0,π])

    f=2,则函数为 f(x)=e^(ax+b)(a∈[−1,1],b∈[−2,0],a+b∈[−2,0])

    f=3,则函数为 f(x)=ax+b(a∈[−1,1],b∈[0,1],a+b∈[0,1])

接下来 m行，每行描述一个事件，事件分为四类。

    appear u v 表示数学王国中出现了一条连接 u 和 v 这两座城市的魔法桥 (0≤u,v<n,u≠v) ，保证连接前 u和 v 这两座城市不能互相到达。

    disappear u v 表示数学王国中连接 u 和 v 这两座城市的魔法桥消失了，保证这座魔法桥是存在的。

    magic c f a b 表示城市 c 的魔法球中的魔法变成了类型为 f ，参数为 a,b 的函数

    travel u v x 表示询问一个智商为 x 的人从城市 u 旅行到城市 v 

（即经过 u到 v 这条路径上的所有城市，包括 u 和 v ）后，他得分的总和是多少。

 若无法从 u 到达 v ，则输出一行一个字符串 unreachable。

1≤n≤100000,1≤m≤200000

Output

对于每个询问，输出一行实数，表示得分的总和。

Sample Input

3 7 C1
1 1 0
3 0.5 0.5
3 -0.5 0.7
appear 0 1
travel 0 1 0.3
appear 0 2
travel 1 2 0.5
disappear 0 1
appear 1 2
travel 1 2 0.5

Sample Output

9.45520207e-001
1.67942554e+000
1.20000000e+000

题解：一看到删边加边那肯定就是LCT了，但是在pushup的时候如何维护这些奇奇怪怪的函数呢？我们需要一种方法将这些函数进行合并，不难想到泰勒展开。

下面列出e和sin的生成函数：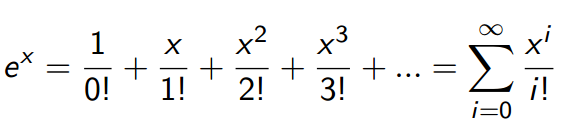

但是题中的x不光有系数，还有常数项，怎么办呢？暴力展开！将公式中的x替换成(ax+b)，然后预处理组合数，用二项式定理暴力展开即可。

实测我们的生成函数大概维护到x^17即可，这样的话我们LCT中的每个节点相当于都要维护它的生成函数以及子树的生成函数和，所以pushup一次就是O(17)的，修改一个节点就是O(17*17)的。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
using namespace std;
const int maxn=100010;
const int D=17;
typedef double db;
int n,m;
char str[100];
int typ[maxn];
db A[maxn],B[maxn],jc[20],c[20][20],at[20],bt[20];
struct node
{
	db v[20],s[20],A,B;
	int fa,ch[2],siz,rev,typ;
	void calc()
	{
		int i,j,f;
		memset(v,0,sizeof(v));
		if(typ==1)
		{
			for(at[0]=bt[0]=1,i=1;i<=D;i++)	at[i]=at[i-1]*A,bt[i]=bt[i-1]*B;
			for(i=1;i<=D;i+=2)
			{
				f=(i%4==1)?1:-1;
				for(j=0;j<=i;j++)	v[j]+=f*at[j]*bt[i-j]*c[i][j]/jc[i];
			}
		}
		if(typ==2)
		{
			for(at[0]=bt[0]=1,i=1;i<=D;i++)	at[i]=at[i-1]*A,bt[i]=bt[i-1]*B;
			for(i=0;i<=D;i++)	for(j=0;j<=i;j++)	v[j]+=at[j]*bt[i-j]*c[i][j]/jc[i];
		}
		if(typ==3)	v[0]=B,v[1]=A;
	}
}s[maxn];
inline bool isr(int x){return s[s[x].fa].ch[0]!=x&&s[s[x].fa].ch[1]!=x;}
inline void pushup(int x)
{
	for(int i=0;i<=D;i++) s[x].s[i]=s[s[x].ch[0]].s[i]+s[s[x].ch[1]].s[i]+s[x].v[i];
	s[x].siz=s[s[x].ch[0]].siz+s[s[x].ch[1]].siz+1;
}
inline void pushdown(int x)
{
	if(s[x].rev)
	{
		swap(s[x].ch[0],s[x].ch[1]);
		if(s[x].ch[0])	s[s[x].ch[0]].rev^=1;
		if(s[x].ch[1])	s[s[x].ch[1]].rev^=1;
		s[x].rev=0;
	}
}
void updata(int x)
{
	if(!isr(x))	updata(s[x].fa);
	pushdown(x);
}
inline void rotate(int x)
{
	int y=s[x].fa,z=s[y].fa,d=(x==s[y].ch[1]);
	if(!isr(y))	s[z].ch[y==s[z].ch[1]]=x;
	s[x].fa=z,s[y].fa=x,s[y].ch[d]=s[x].ch[d^1];
	if(s[x].ch[d^1])	s[s[x].ch[d^1]].fa=y;
	s[x].ch[d^1]=y;
	pushup(y),pushup(x);
}
void splay(int x)
{
	updata(x);
	while(!isr(x))
	{
		int y=s[x].fa,z=s[y].fa;
		if(!isr(y))
		{
			if((x==s[y].ch[0])^(y==s[z].ch[0]))	rotate(x);
			else	rotate(y);
		}
		rotate(x);
	}
}
inline void access(int x)
{
	for(int y=0;x;splay(x),s[x].ch[1]=y,pushup(x),y=x,x=s[x].fa);
}
inline void maker(int x)
{
	access(x),splay(x),s[x].rev^=1;
}
inline void link(int x,int y)
{
	maker(x),s[x].fa=y;
}
inline void cut(int x,int y)
{
	maker(x),access(y),splay(y),s[y].ch[0]=s[x].fa=0,pushup(y);
}
inline int findr(int x)
{
	while(s[x].fa)	x=s[x].fa;
	return x;
}
inline int rd()
{
	int ret=0,f=1;	char gc=getchar();
	while(gc<'0'||gc>'9')	{if(gc=='-')f=-f;	gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret*f;
}
void init()
{
	int i,j;
	for(jc[0]=1,i=1;i<=D;i++)	jc[i]=jc[i-1]*i;
	for(c[0][0]=1,i=1;i<=D;i++)
	{
		c[i][0]=1;
		for(j=1;j<=i;j++)	c[i][j]=c[i-1][j-1]+c[i-1][j];
	}
}
int main()
{
	scanf("%d%d%s",&n,&m,str);
	int i,j,a,b;
	db x,y,ans;
	init();
	for(i=1;i<=n;i++)	scanf("%d%lf%lf",&s[i].typ,&s[i].A,&s[i].B),s[i].calc(),pushup(i);
	for(i=1;i<=m;i++)
	{
		scanf("%s",str);
		if(str[0]=='a')	a=rd()+1,b=rd()+1,link(a,b);
		if(str[0]=='d')	a=rd()+1,b=rd()+1,cut(a,b);
		if(str[0]=='m')	a=rd()+1,splay(a),scanf("%d%lf%lf",&s[a].typ,&s[a].A,&s[a].B),s[a].calc(),pushup(a);
		if(str[0]=='t')
		{
			a=rd()+1,b=rd()+1,scanf("%lf",&x);
			if(findr(a)!=findr(b))
			{
				printf("unreachable\n");
				continue;
			}
			y=1,ans=0,maker(a),access(b),splay(b);
			for(j=0;j<=D;j++,y*=x)	ans+=y*s[b].s[j];
			printf("%.8le\n",ans);
		}
	}
	return 0;
}//1 1 abc 2 1 1 travel 0 0 1