零零星星挖坑几个了，都没填土，实在是欠账太多，闲话少说吧，还是多记录总结一下。今天的主题是围绕convolution和加速

记得之前看过lecun他们组的一篇文章，是fft加速convolution的。按照Convolution Theorem，时域上的卷积可以转成空间域的傅立叶变换进行。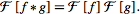

lecun的文章就是通过把卷积变成傅立叶变换实现加速的。从实验里看到，加速比2倍左右。目前这部分有代码开源，但是好像并没有merge到caffe中，原因可能是因为加速比例有限，再者消耗空间。猜测主要是加速比例问题吧，因为加速过程中，由于其原理，当卷积核小，是没什么加速的，当核是3或者5时，速度有的更慢或者相当，而在cnn中卷积的核大多数比较小，起到的加速作用很小，而基于图像处理本身目前的任务来说，卷积核一般不会太大，googlenet用7X7已经是爆炸天了。而从另外一方面来说，对caffe实现多GPU卡的加速或者多机的加速，则是实打实的加速，无论你的卷积核多大，你都能加速。

lecun他们又出了一篇新的文章，facebook的，Fast Convolutional Nets With fbfft: A GPU Performance Evaluation。caffe上已经有人实现了，加速1.4(3X3)到14.5倍。从他们的文章中看到，卷积核小的时候也是实现了加速了，赞。

待续……

convolution,fft, 加速的更多相关文章

  1. 51nod 算法马拉松 34 Problem D 区间求和2 （FFT加速卷积）

    题目链接  51nod 算法马拉松 34  Problem D 在这个题中$2$这个质数比较特殊,所以我们先特判$2$的情况,然后仅考虑大于等于$3$的奇数即可. 首先考虑任意一个点对$(i, j)$ ...

  2. P1919 FFT加速高精度乘法

    P1919 FFT加速高精度乘法 传送门:https://www.luogu.org/problemnew/show/P1919 题意: 给出两个n位10进制整数x和y,你需要计算x*y. 题解: 对 ...

  3. SPOJ - VFMUL - Very Fast Multiplication FFT加速高精度乘法

    SPOJ - VFMUL:https://vjudge.net/problem/SPOJ-VFMUL 这是一道FFT求高精度的模板题. 参考:https://www.cnblogs.com/Rabbi ...

  4. FFT初步学习小结

    FFT其实没什么需要特别了解的,了解下原理,(特别推荐算法导论上面的讲解),模板理解就行了.重在运用吧. 处理过程中要特别注意精度. 先上个练习的地址吧: http://vjudge.net/vjud ...

  5. FFT与多项式、生成函数题目泛做

    题目1 COGS 很强的乘法问题 高精度乘法用FFT加速 #include <cstdlib> #include <iostream> #include <algorit ...

  6. bzoj 3513: [MUTC2013]idiots FFT

    bzoj 3513: [MUTC2013]idiots FFT 链接 bzoj 思路 参考了学姐TRTTG的题解 统计合法方案,最后除以总方案. 合法方案要不好统计,统计不合法方案. \(a+b< ...

  7. 【XSY2166】Hope 分治 FFT

    题目描述 对于一个\(1\)到\(n\)的排列\(a_1,a_2,a_3,\ldots,a_n\),我们定义这个排列的\(P\)值和\(Q\)值: 对于每个\(a_i\),如果存在一个最小的\(j\) ...

  8. 【XSY2332】Randomized Binary Search Tree 概率DP FFT

    题目描述 \(\forall 0\leq i<n\),求有多少棵\(n\)个点,权值和优先级完全随机的treap的树高为\(i\). \(n\leq 30000\) 题解 设\(f_{i,j}\ ...

  9. 【BZOJ3771】Triple 生成函数 FFT 容斥原理

    题目大意 有\(n\)把斧头,不同斧头的价值都不同且都是\([0,m]\)的整数.你可以选\(1\)~\(3\)把斧头,总价值为这三把斧头的价值之和.请你对于每种可能的总价值,求出有多少种选择方案. ...

随机推荐

  1. 更换 npm 源国内镜像 cnpm

    默认镜像源 https://www.npmjs.com/ 临时改变镜像源 方法一:通过config配置指向国内镜像源 npm config set registry http://registry.c ...

  2. suau 公约公倍

    8619 公约公倍 时间限制:500MS  内存限制:1000K 提交次数:475 通过次数:108 题型: 编程题   语言: G++;GCC Description  给定六个正整数a,b,c,d ...

  3. CentOS7/Ubuntu Linux java jdk 环境变量配置

    [root@localhost sony]# tar -zxvf jdk-8u121-linux-x64.tar.gz [root@localhost sony]# .0_121 /usr/local ...

  4. C++中的虚函数表

    (感谢http://blog.csdn.net/haoel/article/details/1948051/) C++中的虚函数的作用主要是实现了多态的机制. 多态,简而言之就是用父类型别的指针指向其 ...

  5. Flask文件目录----- auth/blog 文件

    import functools from flask import (Blueprint, flash, g, redirect, render_template, url_for, request ...

  6. 安装office提示Office 16 Click-to-Run Extensibility Component

    今天安装office时,提示Office 16 Click-to-Run Extensibility Component或者Office 15 Click-to-Run Extensibility C ...

  7. 使用swagger时遇到的问题

    后端写好接口后开始和前端进行联调,为了减少时间成本或者说是后端不想写文档,所以便想使用一套可以自动化生成api接口文档的工具,swagger正是可以解决这一需求.于是很早之前就想把swagger集成到 ...

  8. OpenCart-2.3 (Ubuntu 16.04)

      平台: Ubuntu 类型: 虚拟机镜像 软件包: opencart-2.3 commercial ecommerce opencart open-source 服务优惠价: 按服务商许可协议 云 ...

  9. MySQL的prompt不生效的问题

    安装完MySQL之后,使用了自定义的配置文件来启动MySQL,发现配置在[mysql]中的prompt并没有生效 [root@MySQL56_L1 ~]# /usr/local/mysql/bin/m ...

  10. （原创）北美信用卡(Credit Card)个人使用心得与总结（个人理财版） [精华]

    http://forum.chasedream.com/thread-766972-1-1.html 本人2010年 8月F1 二度来美,现在credit score 在724-728之间浮动,最高的 ...