Codeforces 478D Red-Green Towers：dp

题目链接：http://codeforces.com/problemset/problem/478/D

题意：

　　给你r个红方块和g个绿方块，让你用这些方块堆一个塔。

　　最高层有1个方块，每往下一层块数+1，同时要保证每层中的方块都是同一种颜色。

　　如图：

　　

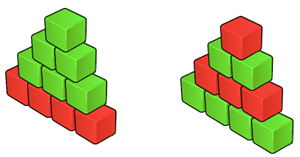
　　问你在塔的高度最高的前提下，堆出塔的方案数。

题解：

　　假设塔最高能堆d层，则：

　　　　d*(d+1)/2 <= r+g

　　解得：

　　　　d = floor((-1+sqrt(1+8*(r+g)))/2)

　　　　并且d最大不超过900。

　　表示状态：

　　　　dp[i][j] = numbers

　　　　表示已经堆了最上面的i层，用了j个红方块，此时的方法数。

　　

　　找出答案：

　　　　ans = ∑ dp[d][max(0,d*(d+1)/2-g) to r]

　　　　因为最终还要保证用了绿方块的个数 <= g，所以枚举i至少要从d*(d+1)/2-g开始。

　　如何转移：

　　　　dp[i][j] = dp[i-1][j] + dp[i-1][j-i]

　　　　从上往下数第i层可能全用绿色，或全用红色

　　边界条件：

　　　　dp[0][0] = 1

　　另外要用滚动数组，否则会MLE。

AC Code:

 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #include <math.h>
 #define MAX_D 900
 #define MAX_R 200005
 #define MOD 1000000007
 #define EPS 1e-5

 using namespace std;

 int r,g,d;
 int dp[][MAX_R];

 int main()
 {
     cin>>r>>g;
     d=floor((-1.0+sqrt(1.0+8.0*(r+g))+EPS)/2.0);
     memset(dp,,sizeof(dp));
     dp[][]=;
     for(int i=;i<=d;i++)
     {
         for(int j=;j<=r;j++)
         {
             dp[i&][j]=dp[(i-)&][j];
             if(j-i>=) dp[i&][j]+=dp[(i-)&][j-i];
             dp[i&][j]%=MOD;
         }
     }
     int ans=;
     for(int i=max(,d*(d+)/-g);i<=r;i++)
     {
         ans=(ans+dp[d&][i])%MOD;
     }
     cout<<ans<<endl;
 }