遗传算法解决TSP问题

1实验环境

实验环境：CPU i5-2450M@2.50GHz，内存6G，windows7 64位操作系统

实现语言：java (JDK1.8)

实验数据：TSPLIB，TSP采样实例库中的att48数据源

数据地址：http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/att48.tsp.gz

TSPLIB是一个从各种来源和各种类型中产生的TSP及其相关问题的采样实例库，这里选取TSP采样实例库中的att48数据源，最优值为10628。该数据源中有48个地点坐标，实验过程是基于这48个坐标求解TSP问题。

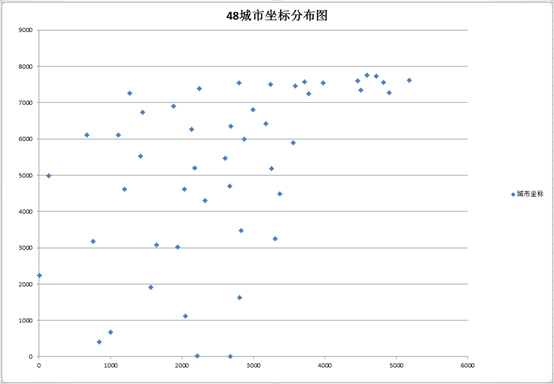
2 TSP问题回顾

旅行商问题，即TSP问题（Travelling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

3 TSP问题常见解法

算法	优点	缺点
穷举法（暴力）	实现简单	时间和空间复杂度太大，不适合解决城市数太多的情况。
贪心算法	实现简单、计算速度快	容易得出局部最优解而不是全局最优解。
动态规划	随着城市数的增加，计算量大大减少，得到了中间各点到终点的最短路径。	同样不适合处理城市数太多的情况。

以上三种常见算法都各自的问题，穷举法和动规不能解决城市数多的情况，而贪心法在城市数少的时候都有可能得不到全局最优解，那么是否存在既能解决城市数多的情况又能得到最优呢？遗传算法。

4遗传算法

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

5 算法实现步骤

5.1初始化阶段

初始化对象：种群规模、城市数量、运行代数、交叉概率、变异概率

初始化数据：读入数据源，将坐标转换为距离矩阵（标准化欧式距离）

初始化种群：随机生成n个路径序列，n表示种群规模。

5.2.计算种群适应度

这里表示每条路径求和。

5.3计算累计概率

计算初始化种群中各个个体的累积概率

5.4迭代

选择算子：赌轮选择策略挑选下一代个体。

交叉运算：第k个算子和k+1个算子有一定的概率交叉变换，k=0、2、4、...、2n

变异运算：每个算子有一定概率基因多次对换，概率处决与变异概率

计算新的种群适应度以及个体累积概率，并更新最优解。

将新种群newGroup复制到旧种群oldGroup中，准备下一代进化（迭代）

5.5输出

输出迭代过程中产生的最短路径长度、最短路径出现代数、以及最短路径

6关键算法

6.1 赌轮选择算法

又称比例选择方法．其基本思想是：各个个体被选中的概率与其适应度大小成正比．

具体操作如下：
(1)计算出群体中每个个体的适应度f(i=1，2，…，M)，M为群体大小；
(2)计算出每个个体被遗传到下一代群体中的概率；

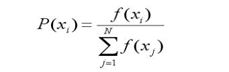
(3)计算出每个个体的累积概率；

（q[i]称为染色体x[i] (i=1, 2, …, n)的积累概率）

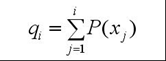
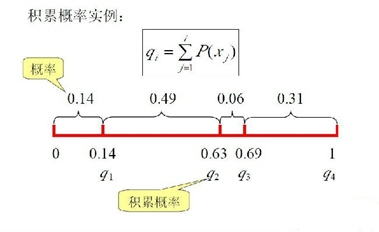
(4)在[0，1]区间内产生一个均匀分布的伪随机数r

(5)若r<q[1]，则选择个体1，否则，选择个体k，使得：q[k-1]<r≤q[k]
成立；

(6)重复(4)、(5)共M次

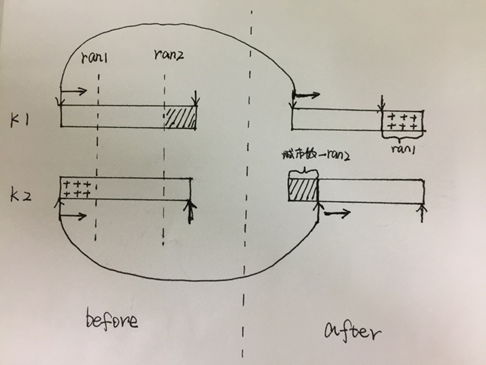
6.2交叉算法

第k（k=0、2、4、...、2n）个算子和k+1个算子有一定的概率交叉变换，这个概率就是交叉概率。

6.3变异算法

每个算子有一定概率（变异概率）基因多次对换。

对一个算子，随机生成两个不相等的范围在[1,城市数]之间的随机整数。将该算子在这两个随机整数对应的位置的城市编号对换，进行上述n次对换，n也是一个[1,城市数]之间的随机整数。

7程序结果分析

主要参数：种群规模、城市数量、最大运行代数、交叉概率、变异概率

7.1种群规模对结果的影响

不变参数

最大运行代数	城市数量	交叉概率	变异概率
1000	10	0.9	0.09

10个城市最短长度为6178，路径：3->9->4->5->6->8->7->0->2->1->3

变参：种群规模

种群规模分别为10、20、30、40、50、100时的运行结果看excel-
sheet1

结论：上述情况下，当种群规模大于等于30的时候算法基本能得到正确解，达到40算法能100%得到最短路径，但是最佳路径出现代数并不稳定，当种群规模达到1000时稳定在50代之内得到正确结果。

7.2最大运行代数对结果的影响

不变参数

种群规模	城市数量	交叉概率	变异概率
30	10	0.9	0.09

10个城市最短长度为6178，路径：3->9->4->5->6->8->7->0->2->1->3

变参：最大运行代数

最大运行代数分别为50、100、200、300、500、1000、10000时的运行结果看excel- sheet2

结论：

上述情况下，当最大运行代数达到1000时算法运行结果趋于稳定(稳定得到最短路径)，这时算法的效率比较高。

当达到10000时100%正确，但是最佳路径出现代数稳定在2000代以内，所以想要2000代之后的计算都是不必要的，算法的最大运行代数最优参数为2000。

7.3城市数量对结果的影响

不变参数

种群规模	最大运行代数	交叉概率	变异概率
30	1000	0.9	0.09

变参：城市数量

城市数量分别为5、8、10、12、15、48时的运行结果看excel-
sheet2

结论：上述情况下，当城市数量<=8时，算法100%的到正确解。当城市数量达到12时，这套参数已经不能得到最优解了，必须调整某些参数。调整分以下情况：

（1）其他参数不变，种群规模逐渐调到120时，算法结果稳定。

（2）其他参数不变，最大运行代数逐渐调到10000时，算法结果稳定。

（3）其他参数不变，交叉概率不管怎么调，算法都得不到最优解。但是将种群规模调大到40，交叉概率调为0.1时，算法结果趋于稳定

综合（1）（2）（3）发现似乎一开始交叉概率就有问题，对于该算法交叉概率应该调低。当交叉概率较高时无论是提高种群规模还是最大运行代数，代价都太大。

当城市数量为48时（最优解10628）

（1）

种群规模	最大运行代数	交叉概率	变异概率
1000	10000	0.1	0.09

算法运行时间为6s，算法结果（10937）优于贪心结果（12842），很接近了，但不是最优。

谢 谢！     未 完 待 续 ...