boosting 是一种将弱分类器转化为强分类器的方法统称，而adaboost是其中的一种，或者说AdaBoost是Boosting算法框架中的一种实现

https://www.zhihu.com/question/37683881

gdbt(Gradient Boosting Decision Tree，梯度提升决策树)

gbdt通过多轮迭代,每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练。

弱分类器一般会选择为CART TREE（也就是分类回归树）。由于上述高偏差和简单的要求 每个分类回归树的深度不会很深。最终的总分类器 是将每轮训练得到的弱分类器加权求和得到的（也就是加法模型）。

模型最终可以描述为：

　　　　　　　　

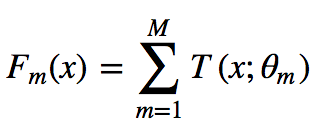
模型一共训练M轮，每轮产生一个弱分类器 T(x;θm)。弱分类器的损失函数

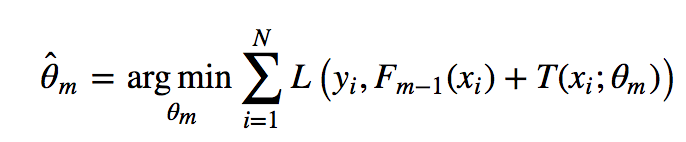
　　看公式就知道其实每次学习的是T，即当前的那个分类器

Fm−1(x)为当前的模型，gbdt 通过经验风险极小化来确定下一个弱分类器的参数。具体到损失函数本身的选择也就是L的选择，有平方损失函数，0-1损失函数，对数损失函数等等。如果我们选择平方损失函数，那么这个差值其实就是我们平常所说的残差。

    • 但是其实我们真正关注的，1.是希望损失函数能够不断的减小，2.是希望损失函数能够尽可能快的减小。所以如何尽可能快的减小呢？
    • 让损失函数沿着梯度方向的下降。这个就是gbdt 的 gb的核心了。 利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值去拟合一个回归树。gbdt 每轮迭代的时候，都去拟合损失函数在当前模型下的负梯度。
    • 这样每轮训练的时候都能够让损失函数尽可能快的减小，尽快的收敛达到局部最优解或者全局最优解。

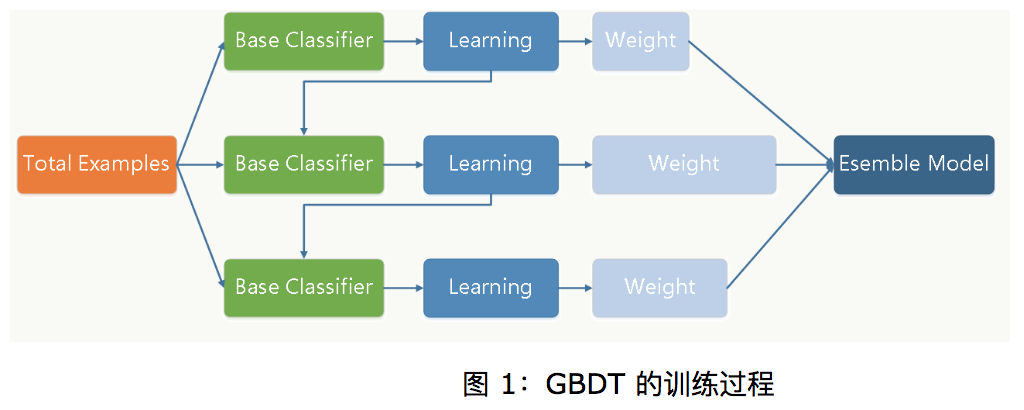
首先明确gbdt也属于boosting，但他和adboost不同，他不是每次训练部门数据，而是整个数据集(如上图所示)。那他为什么又属于boosting呢？个人认为：1.gdbt也是串行的 2.每次迭代需要上次的返回结果，这是这里的返回结果和adboost不同。(之前认为总分类器是将每轮训练得到的弱分类器加权求和得到的，但bagging是vote或者求平均。但是后来发现，bagging里面vote也可以通过软vote获得加权和)

https://www.cnblogs.com/ModifyRong/p/7744987.html

区别：1.adboost是优化错分数据权重,gdbt是通过残差优化每一轮的分类器

　　   2.adboost是指数损失函数，gdbt是平方损失函数

gdbt与adboost(或者说boosting)区别的更多相关文章

  1. Boosting学习笔记（Adboost、GBDT、Xgboost）

    转载请注明出处:http://www.cnblogs.com/willnote/p/6801496.html 前言 本文为学习boosting时整理的笔记,全文主要包括以下几个部分: 对集成学习进行了 ...

  2. RF 和 GBDT联系和区别

    1.RF 原理 用随机的方式建立一个森林,森林里面有很多的决策树,随机森林的每一棵决策树之间是没有关联的.在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看 ...

  3. bagging and boosting

    bagging 侧重于降低方差 方差-variance 方差描述的是预测值的变化范围,离散程度,也就是离期真实值的距离.方差过大表现为过拟合,训练数据的预测f-score很高,但是验证或测试数据的预测 ...

  4. rf, xgboost和GBDT对比；xgboost和lightGbm

    1. RF 随机森林基于Bagging的策略是Bagging的扩展变体,概括RF包括四个部分:1.随机选择样本(放回抽样):2.随机选择特征(相比普通通bagging多了特征采样):3.构建决策树:4 ...

  5. 随机森林和GBDT

    1. 随机森林 Random Forest(随机森林)是Bagging的扩展变体,它在以决策树 为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机特征选择,因此可以概括RF ...

  6. RF,GBDT,XGBoost,lightGBM的对比

    转载地址:https://blog.csdn.net/u014248127/article/details/79015803 RF,GBDT,XGBoost,lightGBM都属于集成学习(Ensem ...

  7. AI面试刷题版

    (1)代码题(leetcode类型),主要考察数据结构和基础算法,以及代码基本功 虽然这部分跟机器学习,深度学习关系不大,但也是面试的重中之重.基本每家公司的面试都问了大量的算法题和代码题,即使是商汤 ...

  8. AI涉及到数学的一些面试题汇总

    [LeetCode] Maximum Product Subarray的4种解法 leetcode每日解题思路 221 Maximal Square LeetCode:Subsets I II (2) ...

  9. Jackknife，Bootstraping, bagging, boosting, AdaBoosting, Rand forest 和 gradient boosting的区别

    引自http://blog.csdn.net/xianlingmao/article/details/7712217 Jackknife,Bootstraping, bagging, boosting ...

随机推荐

  1. [LeetCode]Longest Substring Without Repeating Characters题解

    Longest Substring Without Repeating Characters: Given a string, find the length of the longest subst ...

  2. 系统每隔一段时间自动pull代码

    #!/bin/bash while true;do dd=$( date -u ) echo $dd,"start pull wmsinventoryapiwms6.2" cd / ...

  3. Spring入门（四）— 整合Struts和Hibernate

    一.Spring整合Struts 1. 初步整合 只要在项目里面体现spring和 strut即可,不做任何的优化. struts 环境搭建 创建action public class UserAct ...

  4. MySQL的预编译功能

      1.预编译的好处 大家平时都使用过JDBC中的PreparedStatement接口,它有预编译功能.什么是预编译功能呢?它有什么好处呢? 当客户发送一条SQL语句给服务器后,服务器总是需要校验S ...

  5. MyBatis 事务源码分析

    先来看看在JAVA事务的相关技术,在JAVA中有两类事务,JDBC事务和JTA事务,如果是JDBC类型的事务,则是由Connection类来控制的.如果创建一个Connection对象时,没有显示调用 ...

  6. HTML新手推荐

    对于前端的学习要先了解一下浏览器和html的发展史其次看看这篇文章:https://kb.cnblogs.com/page/129756/#chapter1我读到这句话时候感觉到了科技这个东西有很多时 ...

  7. PHP在foreach中对$value赋值无效，应该用 ‘键’ 或者 &$value的形式

    首先我们看下这段代码: foreach ($data as$value) { $value['name'] = 'Hehe'; } $data中原始的数据为: array(1) { [0] => ...

  8. 毕向东_Java基础视频教程第21天_IO流（1）

    第21天-01-IO流(对象的序列化) ObjectInputStream与ObjectOutputStream 被操作的对象需要实现Serializable接口(标记接口) 非必须, 但强烈建议所有 ...

  9. 小程序UI

    从input组件说起 <input maxlength="10" placeholder="最大输入长度10" /> <div id=&quo ...

  10. sql 2000 无法连接远程数据库 sqlserver不存在或访问被拒绝、不能打开到主机的连接，在端口1433：连接失败等 解决方案

    问题: sql 2000 无法连接远程数据库 sqlserver不存在或访问被拒绝 telnet 127.0.0.1 1433     提示:不能打开到主机的连接,在端口1433:连接失败 解决方案: ...