考试题 T2

题意分析

首先 要求起点终点不连通

再结合数据范围 就是最小割了

首先我们可以建一个图出来

如果\(x\)可以到\(y\)的话

那么我们就从\(x\)向\(y\)连一条代价为\(h[x]-h[y]+1\)的边 代表不联通的代价

可是如果存在以下情况呢

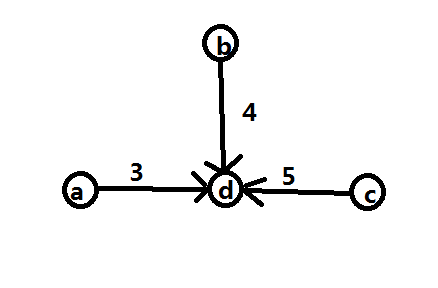
如果我们选择切断\(c\)到\(d\)的边的话

实际上我们也切断了\(a\)到\(c\)以及\(b\)到\(c\)

所以我们可以这么建

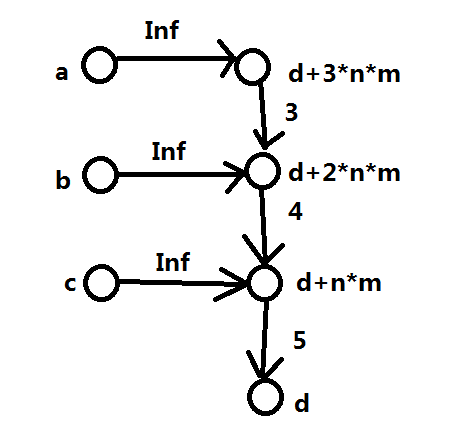
然后跑最大流就可以了

由于起点以及终点不可以被修改

所以我忽视了别的点到起点的连边

同时别的点到终点的连边边权都是\(inf\)

CODE:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<string>
#include<queue>
#include<map>
#include<stack>
#include<list>
#include<set>
#include<deque>
#include<vector>
#include<ctime>
#define ll long long
#define inf 0x7fffffff
#define N 88
#define IL inline
#define M 5008611
#define D double
#define ull unsigned long long
#define R register
using namespace std;
template<typename T>IL void read(T &_)
{
    T __=0,___=1;char ____=getchar();
    while(!isdigit(____)) {if(____=='-') ___=0;____=getchar();}
    while(isdigit(____)) {__=(__<<1)+(__<<3)+____-'0';____=getchar();}
    _=___ ? __:-__;
}
/*-------------OI使我快乐-------------*/
int T;ll ans;
int n,m,tot=1,sx,sy,tx,ty;
int hei[N][N],to[M],nex[M],head[N*N*5],w[M];
int dep[5*N*N],cur[5*N*N];
vector<pair<int,int> > G[N*N];
queue<int> Q;
bool vis[N][N];
int tox[6]={0,0,0,1,-1},toy[6]={0,1,-1,0,0};
IL int id(int x,int y){return (x-1)*m+y;}
IL bool safe(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m;}
IL void add(int x,int y,int z)
{to[++tot]=y;nex[tot]=head[x];head[x]=tot;w[tot]=z;
swap(x,y);to[++tot]=y;nex[tot]=head[x];head[x]=tot;w[tot]=0;}
IL bool bfs()
{
	for(R int i=1;i<=5*n*m;++i) dep[i]=0;
	Q.push(id(sx,sy));dep[id(sx,sy)]=1;
	for(;!Q.empty();)
	{
		int u=Q.front();Q.pop();
		for(R int i=head[u];i;i=nex[i])
		{
			int v=to[i];
			if(w[i]>0&&dep[v]==0)
			{
				dep[v]=dep[u]+1;Q.push(v);
			}
		}
	}
	return dep[id(tx,ty)]!=0;
}
IL int dfs(int now,int res)
{
	if(now==id(tx,ty)||res==0) return res;
	for(R int &i=cur[now];i;i=nex[i])
	{
		int v=to[i];
		if(w[i]>0&&dep[v]==dep[now]+1)
		{
			int have=dfs(v,min(w[i],res));
			if(have>0)
			{
				w[i]-=have;w[i^1]+=have;
				return have;
			}
		}
	}
	return 0;
}
IL void Dinic()
{
	while(bfs())
	{
		for(R int i=1;i<=5*n*m;++i) cur[i]=head[i];
		int d=dfs(id(sx,sy),inf);
		while(d) ans+=d,d=dfs(id(sx,sy),inf);
	}
}
int main()
{
	freopen("ski.in","r",stdin);
	freopen("ski.out","w",stdout);
	read(T);
	while(T--)
	{
		read(n);read(m);read(sx);read(sy);read(tx);read(ty);
		tot=1;ans=0;memset(head,0,sizeof head);
		for(R int i=1;i<=n;++i)
		 for(R int j=1;j<=m;++j)
		  read(hei[i][j]);
		if(abs(sx-tx)+abs(sy-ty)==1) {puts("-1");continue;}
		for(R int i=1;i<=n;++i)
		{
		 for(R int j=1;j<=m;++j)
		  for(R int k=1;k<=4;++k)
		  {
		  	int nowx=i+tox[k],nowy=j+toy[k];
		  	if(nowx==sx&&nowy==sy) continue;
		  	if(safe(nowx,nowy)&&hei[nowx][nowy]<=hei[i][j])
		  	G[id(nowx,nowy)].push_back(make_pair(hei[i][j]-hei[nowx][nowy]+1,id(i,j)));
		  }
		}
		for(R int i=1;i<=n*m;++i)
		{
			if(G[i].size())
			sort(G[i].begin(),G[i].end());
		}
//		for(R int i=1;i<=n*m;++i)
//		{
//			if(G[i].size())
//			{
//				for(R int j=0;j<(int)G[i].size();++j)
//				printf("%d -- %d --> %d\n",G[i][j].second,G[i][j].first,i);
//			}
//		}
		for(R int i=1;i<=n*m;++i)
		{
			int now=0;
			if(id(tx,ty)==i)
			{
				for(R int j=(int)G[i].size()-1;j>=0;--j)
				{
//					printf("%d -- %d --> %d\n",G[i][j].second,G[i][j].first,i);
					++now;
					add(G[i][j].second,i+now*n*m,inf);
					add(i+now*n*m,i+(now-1)*n*m,inf);
				}
			}
			else
			{
				for(R int j=(int)G[i].size()-1;j>=0;--j)
				{
//					printf("%d -- %d --> %d\n",G[i][j].second,G[i][j].first,i);
					++now;
					add(G[i][j].second,i+now*n*m,inf);
					add(i+now*n*m,i+(now-1)*n*m,G[i][j].first);
				}
			}
		}
		Dinic();
		printf("%lld\n",ans);
		for(R int i=1;i<=n*m;++i) G[i].clear();
	}
	fclose(stdin);
	fclose(stdout);
    return 0;
}

HEOI 2019 RP++