A*寻路算法详细解读

文章目录

A*算法描述

简化搜索区域
概述算法步骤
进一步解释

具体寻路过程
模拟需要更新F值的情况
Lua代码实现

在学习A*算法之前，很好奇的是A*为什么叫做A*。在知乎上找到一个回答，大致意思是说，在A*算法之前有一种基于启发式探索的方法来提高Dijkstra算法的速度，这个算法叫做A1。后来的改进算法被称为A*。*这个符号是从统计文献中借鉴来的，用来表示相对一个旧有标准的最优估计。

启发式探索是利用问题拥有的启发信息来引导搜索，达到减少探索范围，降低问题复杂度的目的。

A*寻路算法就是启发式探索的一个典型实践，在寻路的过程中，给每个节点绑定了一个估计值（即启发式），在对节点的遍历过程中是采取估计值优先原则，估计值更优的节点会被优先遍历。所以估计函数的定义十分重要，显著影响算法效率。

A*算法描述

简化搜索区域

将待搜索的区域简化成一个个小方格，最终找到的路径就是一些小方格的组合。当然是可以划分成任意形状，甚至是精确到每一个像素点，这完全取决于你的游戏的需求。一般情况下划分成方格就可以满足我们的需求，同时也便于计算。
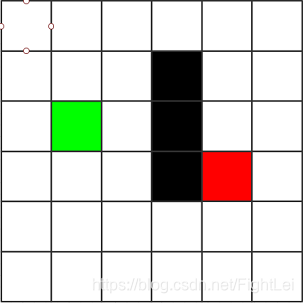
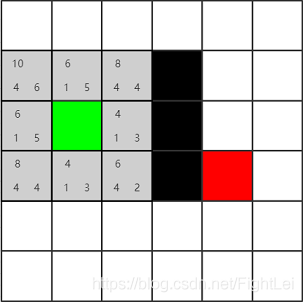
如下图区域，被简化成6*6的小方格。其中绿色表示起点，红色表示终点，黑色表示路障，不能通行。

概述算法步骤

先描述A*算法的大致过程：

将初始节点放入到open列表中。
判读open列表。如果为空，则搜索失败。如果open列表中存在目标节点，则搜索成功。
从open列表中取出F值最小的节点作为当前节点，并将其加入到close列表中。
计算当前节点的相邻的所有可到达节点，生成一组子节点。对于每一个子节点：
- 如果该节点在close列表中，则丢弃它
- 如果该节点在open列表中，则检查其通过当前节点计算得到的F值是否更小，如果更小则更新其F值，并将其父节点设置为当前节点。
- 如果该节点不在open列表中，则将其加入到open列表，并计算F值，设置其父节点为当前节点。
转到2步骤

进一步解释

初始节点，目标节点，分别表示路径的起点和终点，相当于上图的绿色节点和红色节点
F值，就是前面提到的启发式，每个节点都会被绑定一个F值
F值是一个估计值，用F(n) = G(n) + H(n) 表示，其中G(n)表示由起点到节点n的固定消耗，H(n)表示节点n到终点的估计消耗。H(n)的计算方式有很多种，比如曼哈顿H(n) = x + y，或者欧几里得式H(n) = sqrt(x^2 + y^2)。本例中采用曼哈顿式。
F(n)就表示由起点经过n节点到达终点的总消耗
为了便于描述，本文在每个方格的左下角标注数字表示G(n)，右下角数字表示H(n)，左上方数字表示F(n)。具体如何计算请看下面的一个例子

具体寻路过程

接下来，我们严格按照A*算法找出从绿色节点到红色节点的最佳路径
首先将绿色节点加入到open列表中
接着判断open列表不为空（有起始节点），红色节点不在open列表中
然后从open列表中取出F值最小的节点，此时，open列表中只有绿色节点，所以将绿色节点取出，作为当前节点，并将其加入到close列表中
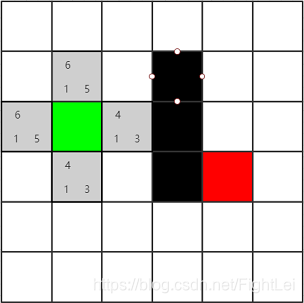
计算绿色节点的相邻节点（暂不考虑斜方向移动），如下图所示的所有灰色节点，并计算它们的F值。这些子节点既没有在open列表中，也没有在close列表中，所以都加入到open列表中，并设置它们的父节点为绿色节点

F值计算方式：
以绿色节点右边的灰色节点为例
G(n) = 1，从绿色节点移动到该节点，都只需要消耗1步
H(n) = 3，其移动到红色节点需要消耗横向2步，竖向一步，所以共消耗3步（曼哈顿式）
F(n) = 4 = G(n) + H(n)

试着算一下其他灰色节点的F值吧，看看与图上标注的是否一致

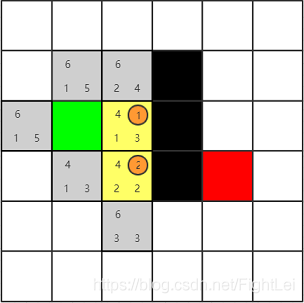
继续选择open列表中F值最小的节点，此时最小节点有两个，都为4。这种情况下选取哪一个都是一样的，不会影响搜索算法的效率。因为启发式相同。这个例子中按照右下左上的顺序选取（这样可以少画几张图(Ｔ▽Ｔ)）。先选择绿色节点右边的节点为当前节点，并将其加入close列表。其相邻4个节点中，有1个是黑色节点不可达，绿色节点已经被加入close列表，还剩下上下两个相邻节点，分别计算其F值，并设置他们的父节点为黄色节点。

此时open列表中F值最小为4，继续选取下方节点，计算其相邻节点。其右侧是黑色节点，上方1号节点在close列表。下方节点是新扩展的。主要来看下左侧节点，它已经在open列表中了。根据算法我们要重新计算它的F值，按经过2号节点计算H(n) = 3，G(n)不变，所以F(n) = 6相比于原值反而变大了，所以什么也不做。（后面的步骤中重新计算F值都不会更小，不再赘述）

此时open列表中F值最小仍为4，继续选取

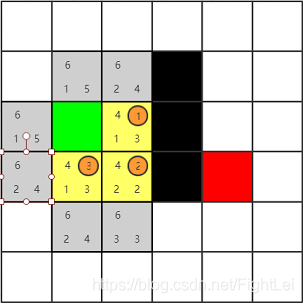
此时open列表中F值最小为6，优先选取下方节点

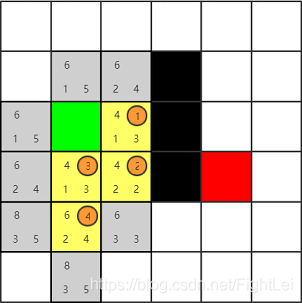
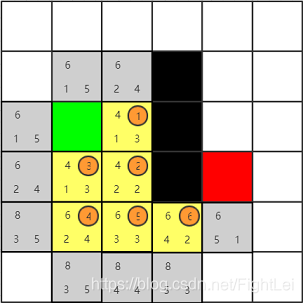
此时open列表中F值最小为6，优先选取右方节点

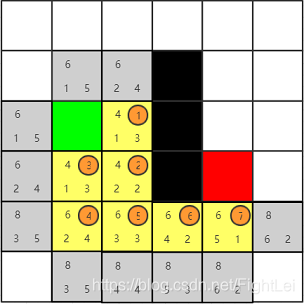
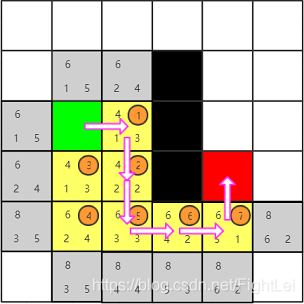
此时我们发现红色节点已经被添加到open列表中，算法结束。从红色节点开始逆推，其父节点为7号，7号父节点为6号，6号父节点为5号…，最终得到检索路径为：绿色-1-2-5-6-7-红色

模拟需要更新F值的情况

在上面的例子中，所有遇到已经在open列表中的节点重新计算F值都不会更小，无法做更新操作。
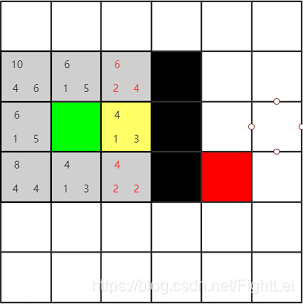
所以再举一个例子来演示这种情况。相同的搜索区域，假设竖向或横向移动需要消耗1，这次也支持斜方向移动了，但是斜方向可能都是些山路不好走，移动一次需要消耗4。对应的相邻节点F值如下图所示

同样选择open列表中F值最小的节点，我们优先选择了右方节点，计算其相邻节点。共8个。其中三个是黑色节点，一个绿色节点在close列表中，不考虑。上方两个和下方两个都是已经在open列表中了，要重新计算F值。
先看左上角的相邻节点，通过黄色节点到达改节点，H(n) = 5，G(n)不变，F(n)反而更大了，所以什么也不做。左下角节点同理。
上方居中节点，通过黄色节点计算H(n) = 2, G(n)不变，F(n) = 6 < 8 所以，更新这个节点的F值，并将其父节点修改为黄色节点。下方居中节点同理。

Lua代码实现

写了一套A*算法的Lua实现。主要特点如下：

优化效率，采用了map缓存，避免多次循环遍历
支持配置移动权重
支持配置是否可以斜向移动，斜向时墙角是否可通行

源码请查看：https://github.com/iwiniwin/LuaKit/blob/master/AStar.lua