KMP算法匹配原理以及C++实现

原创作品，转载请注明出处:点我

假设A表示目标字符串，A="abababaababacb"，B表示匹配模式，B="ababacb"

用两个指针i和j分别表示，A[i-j+1 .... i]与B[1...j]完全相等。也就是说，i是不断增加的，随着i的增加j相应的变化，且满足以A[i]结尾的长度为j的字符串正好匹配B串的前j个字符(j当然越大越好)，现在需要jianyanA[i+1]和B[j+1]的关系。当A[i+1]=B[j+1]时，i和j各自增加一，什么时候j=m了，我们就说B是A的子串(B串已经完整了)，并且跟根据这使得i值算出匹配的位置。当A[i+1]<>B[j+1]，KMP的策略是调整j的位置(减小j值)使得A[i-j+1...i]与B[1...j]保持匹配且新的B[j+1]恰好与A[i+1]匹配。

i  = 1  2  3  4  5     7  8  9 10 11 12 13  14

A = a  b  a  b  a  b  a  a  b  a   b   a   c   b

B = a  b  a  b  a  c  b

j  = 1  2  3  4  5    7

当i，j等于5时，A[i+1]跟B[j+1]不相等，这是要缩小j为j'(也就是要把B字符串往右移)。我们发现，j'必须要使得B[1...j]中的头j'个字母和末j'个字母完全相等，这样j变成j'后才能继续保持i和j的性质。当然，j'越大越好。当心的j为3时，恰好符合要求。

我们可以知道，新的j可以取多少跟i无关，只与B串有关。我们可以预处理出这样的一个数组P[j]，表示当匹配到B数组的第j个字母而第j+1个字母不能匹配的时候，心的j的最大值是多少。

以B="ababacb"为例，解释P[j]数组的求结果

a b a b a c b

0 0 1 2 3 0 0

1、首字符a，一律设为0，即P[1]=0

2、“ab” 第一个字符为a，最后一个字符为b，不相等，所以长度为0，即P[2]=0

3、“aba”，头两个字符串为“ab”，后两个为"ba"，不相同，头一个字符串为a，后一个也为a,相同，所以长度为1，即P[3]=1

4、"abab"，头两个为ab，后两个为ab，相同，头三个位aba，末尾三个为bab，不同，所以最大长度为2，即P[4]=2

5、"ababa"，头三个位aba，末尾三个也为aba，头四个为abab，末尾四个为baba，不同，所以最大长度为3，即P[5]=3

以此类推，可以得出数组P[j]  

求出了P[j]之后，就可以根据P[j]进行匹配了，还是以上面的A、B为例，匹配过程中用到的几个变量

pattern表示B，Target表示A

headIndex指向A中跟B进行匹配的子串的首字符

targetIndex指向A中正在跟B匹配的字符的索引，patternIndex指向B中正在匹配的字符在B中的索引

targetIndex等于向右移动的位数加上patternIndex，即targetIndex=headIndex-1+patternIndex

第一步、

此时，patternIndex= 1，targetIndex= 1，headIndex=1

此时pattern[patternIndex] == target[targetIndex],然后patternIndex跟targetIndex增加一，再接着比较是否相同

直到targetIndex跟patternIndex为6的时候，pattern[patternIndex] ！= target[targetIndex]

此时，就需要把B向右移动，进行下一次的匹配，那移动多少比较好呢？这就需要根据P[j]来计算

由于此时，patternIndex前面的ababa已经匹配了，P[5]=3，前面匹配的字符串ababa的长度为5，所以字符串pattern向右移动的位数为5-3=2，即pattern向右移动到3，即新的headIndex=headIndex+2=3；而新的patternIndex=P[5]+1=4，即新的patternIndex指向B串中的第四位，targetIndex=headIndex+patternIndex-1=3+4-1=6，所以移动之后的情况如下图

此时，此时pattern[patternIndex] == target[targetIndex],然后patternIndex跟targetIndex增加一，再接着比较是否相同

当patternIndex等于6，targetIndex等于8时，pattern[patternIndex] ！= target[targetIndex]，又要把B串往右移，此时，

P[5]=3，前面的ababa已经匹配，长度为5，所以向右移动的位数为5-3=2，此时，headIndex=headIndex+2=3+2=5，patternIndex=P[5]+1=4，指向B串中的第四位，targetIndex=headIndex+patternIndex-1=5+4-1=8，所以targetIndex指向A串中的第八位

，此时pattern[patternIndex] ！= target[targetIndex]，又要把B串往右移，此时前面的aba已经匹配成功，长度为3，P[3]=1,所以往右移动的长度为3-1=2，移动两位，此时，headIndex=headIndex+2=5+2=7,patternIndex=P[3]+1=1+1=2指向B串中的第二位，targetIndex=headIndex+patternIndex-1=7+2-1=8，指向A串的第八位

，此时pattern[patternIndex] ！= target[targetIndex]，又要把B串往右移，此时前面已经匹配的串为a，长度为1，P[1]=0，往右移动的位数为1-P[1]=1-0=1；

此时，headIndex=headIndex+1=7+1=8，patternIndex=P[1]+1=1，指向B串的第一位，targetIndex=headIndex+patternIndex-1=8+1-1=8，指向A串的第八位，如图所示

此时再一次匹配，就会匹配成功。

下面是KMP算法的C++实现，有点小问题

 #ifndef __KMP__H__
 #define __KMP__H__
 #include <string>
 #include <vector>
 using namespace std;

 class KMP{
 public:
              //void static getNext(const string &str,vector<int> &vec);
              int kmp();
             KMP(){}
             KMP( const string &target,const string &pattern):mTarget(target),mPattern(pattern){}
             void setTarget(const string &target);
             void setPattern(const string &pattern);
 private:
             vector< int> mVec;
             string mTarget;
             string mPattern;
             void getNext();
 };
 #endif

下面是源代码实现

 #include "KMP.h"
 #include <iostream>
 #include <vector>
 using namespace std;

 //获取字符串str的所有子串中相同子集的长度
 //比如字符串ababacb，分别获取字符串a,ab,aba,abab,ababa,ababac,ababacb中D
 //最前面和最后面相同的子串的最大长度，比如
 //a:因为aa为a单个字符，所以最前面和最后面相同的子串的最大长度为a0
 //aba,最前面一个a和最后面一个元a素a相同，所以值为a1，abab最前面2个ab和最后面两个ab相同，值为a2
 //ababa最前面3个为aaba，最后面3个为aaba，所以值为a3
 void KMP::getNext()
 {
       mVec.clear(); //清空?ec
       //vec.push_back(0);//为a了使用方便，vec的第一个数据不用
       mVec.push_back(); //第一个字符的下一个位置一定是0,比如"ababacb",首字符a的值为0
       string::const_iterator start = mPattern.begin();
       string::const_iterator pos = start + ;
       while(pos != mPattern.end())
       {
             string subStr(start,pos+); //获取子字符串
             int strLen = subStr.size() - ;//获取子串中D前后相同的子子串的最大长度
             do
             {
                    string prefix(subStr,,strLen); //获取subStr中D的前面strLen子集
                    string postfix(subStr,subStr.size()-strLen,strLen); //获取subStr中D的前面?trLen子集
                    if(prefix == postfix)
                    {
                            mVec.push_back(strLen);
                            break;
                     }
                     --strLen;
                     /如果前后相同的子集的长度小于一
                     /说明没有相同的，则把0压栈
                     if(strLen < )
                    　　　　mVec.push_back();
              } while(strLen > );

              ++pos;
        }
 }

 void KMP::setPattern(const string &pattern)
 {
       mPattern = pattern;
 }

 void KMP::setTarget(const string &target)
 {
       mTarget = target;
 }

 int KMP::kmp()
 {
      getNext(); //首先获取next数据
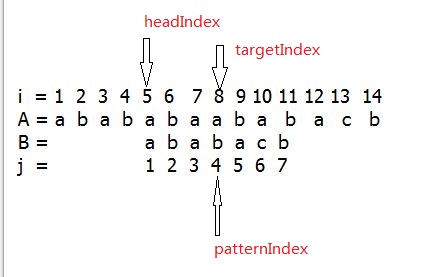
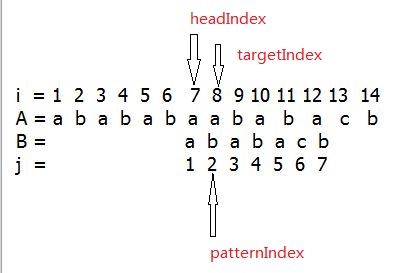
      int targetIndex = ;
      int patternIndex = ;
      int headIndex = ;//指向跟pattern匹配的Target的第一个元素的索引
      while(patternIndex != mPattern.size() && targetIndex != mTarget.size())
      {
            for(int i = ; i < mPattern.size()-;++i)
            {
                   if(mPattern[patternIndex] == mTarget[targetIndex])
                   {
                          ++patternIndex;
                          ++targetIndex;
                          if(mPattern.size()== patternIndex)//如果已经匹配成功，则退出循环
                                  break;
                    }
                    else
                    {
                          if( == patternIndex)//如果第一个字符就不匹配，则把mTarget左移一位
                                   ++headIndex;
                          else
                          {
                                   headIndex += patternIndex - mVec[patternIndex-];//由于vector索引从零开始，所以要减去一
                                   patternIndex = mVec[patternIndex-];//更新patternIndex索引
                          }
                          targetIndex = headIndex + patternIndex;//跟新targetIndex索引
                          break;
                     }

             }
       }

       return headIndex;
 }