Matlab——数值计算——单个代数方程 代数方程组




方程求解
求解单个代数方程
MATLAB具有求解符号表达式的工具,如果表达式不是一个方程式(不含等 号),则在求解之前函数solve将表达式置成等于0。
>> syms a
syms b
syms c
syms x
>> solve('a*x^2+b*x+c') ans = -(b + (b^ - *a*c)^(/))/(*a)
-(b - (b^ - *a*c)^(/))/(*a)
结果是符号向量,其元素是方程的两个解。如果想对非缺省值x变量求解,solve必须指定变量
>> solve('a*x^2+b*x+c','b')
ans =
-(a*x^ + c)/x
带有等号的符号方程也可以求解:
>> f = solve('cos(x) = sin(x)')
f =
pi/
>> t = solve('tan(2*x) = sin(x)')
t =

>> x = solve('exp(x) = tan(x)')
警告: Cannot solve symbolically. Returning a numeric
approximation instead. %不能用符号来解决。返回数字是近似值。
x =
-226.19467105846511316931032359612
代数方程组求解

>> eq1 = 'x-3 =4';
eq2 = 'x*2-x-6=0';
eq3 = 'x^2+2*x+4=0';
eq4 = '3*x+2*y-z=10';
eq5 = '-x+3*y+2*z=5';
eq6='x-y-z=-1';
>> solve(eq1) ans = >> solve(eq2) ans = >> solve(eq3) ans = - ^(/)*i -
^(/)*i - >> solve(eq4,eq5,eq6) ans = x: [1x1 sym]
y: [1x1 sym]
z: [1x1 sym]
这里,solve(eq4,eq5,eq6)是一个结构数组,其中每个元素为一符号类型的量:
>> ff = solve(eq4,eq5,eq6);
>> ff.x ans = - >> ff.y ans = >> ff.z ans = -
也可以:
>> [a,b,c] = solve(eq4,eq5,eq6) a = - b = c = -
例题:

解题思路:
首先,根据以上给出的信息列出一组线性方程,假如p,n,d和q分别表示1美分,5美分,10美分,和25美分的硬币数

>> syms d
>> syms p
>> syms n
>> syms q
>> a = 'd+(n+p)/2=q';
>> b = 'p=n+d+q-10';
>> c = 'q+d = p+n/4';
>> d = 'q+p = n+8*d-1';
>> [pennise,nickles,dimes,quarters] = solve(a,b,c,d,'p,n,d,q')
警告: Do not specify equations and variables as character
strings. Instead, create symbolic variables with syms.
%不要将公式和变量指定为字符串。相反,使用syms创建符号变量。 pennise = nickles = dimes = quarters =

>> money = .*+.*+.*+.*
money =
4.6100

例题:
【0】从三维坐标初步观察两函数图形相交情况
x=-:0.05:;y=x;[X,Y]=meshgrid(x,y); %产生x-y平面上网点坐标
F1=sin(X-Y);F2=cos(X+Y);
F0=zeros(size(X));
surf(X,Y,F1),
xlabel('x'),ylabel('y'), view([-,]),hold on,
surf(X,Y,F2),surf(X,Y,F0),
shading interp,
hold off

【1】在某区域观察两函数0等位线的交点情况
x=-:0.5:;y=x;[X,Y]=meshgrid(x,y); %产生x-y平面上网点坐标
F1=sin(X-Y);F2=cos(X+Y);
v=[-0.2, , 0.2]; %指定三个等位值,是为了更可靠地判断0等位线的存在。
contour(X,Y,F1,v) %画F1的三条等位线。
hold on,contour(X,Y,F2,v),hold off %画F2的三条等位线。
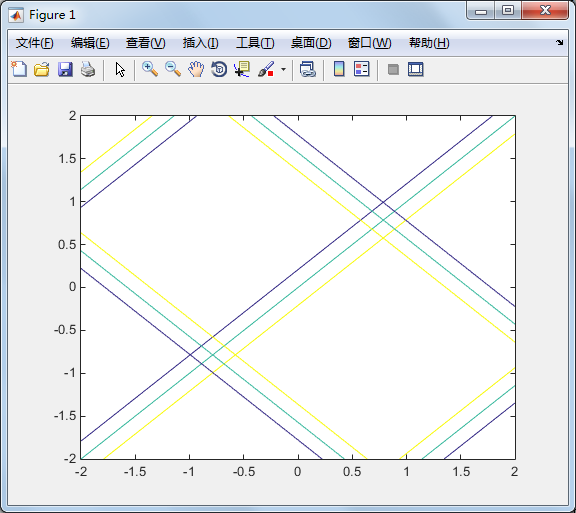
【2】从图形获取零点的初始近似值
用ginput 获取两个函数0 等位线(即三线组中间那条线)交点的坐标。
[x0,y0]=ginput(); %在图上取两个点的坐标
disp([x0,y0])

【3】利用 fsolve 求精确解(以求(0.7926,7843)附近的解为例。)
本例直接用字符串表达被解函数。注意:在此,自变量必须写成x(1), x(2)。
假如写成xy(1), xy(2),指令运行将出错。
fun='[sin(x(1)-x(2)),cos(x(1)+x(2))]'; %<>
xy=fsolve(fun,[x0(),y0()])
%<>
xy =
0.7854 0.7854
【4】检验
fxy1=sin(xy()-xy());fxy2=cos(xy()+xy());disp([fxy1,fxy2])
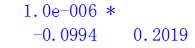

Matlab——数值计算——单个代数方程 代数方程组的更多相关文章
- MATLAB数值计算——0
目录 MATLAB数值计算 1.solve() 2.fzero() 3.fsolve() MATLAB数值计算 MATLAB中文论坛基础板块常见问题归纳(出处: MATLAB中文论坛) 登录http: ...
- fslove - Matlab求解多元多次方程组
fslove - Matlab求解多元多次方程组 简介: 之前看到网上的一些资料良莠不齐,各种转载之类的,根本无法解决实际问题,所以我打算把自己的学到的总结一下,以实例出发讲解fsolve. 示例如下 ...
- Matlab数值计算最简单的一个例子——指数衰减
放射性衰变是指数衰减的典型例子.另外还有化学反应某反应物的减少,RC电路电流的减小,大气压随海拔高度的减小等. 指数衰减的方程: \begin{equation} \frac{dN(t)}{dt}=- ...
- Matlab数值计算示例: 牛顿插值法、LU分解法、拉格朗日插值法、牛顿插值法
本文源于一次课题作业,部分自己写的,部分借用了网上的demo 牛顿迭代法(1) x=1:0.01:2; y=x.^3-x.^2+sin(x)-1; plot(x,y,'linewidth',2);gr ...
- matlab解三元二次方程组
C1=7.0863; C2=6.8971; C3=0.4929; C4=0.8131; C5=1.8240; C6=3.8108; C7=3.7318; C8=-2.2238; C9=1.9905; ...
- Matlab 数值计算
本博客记录一些简单的计算 det(A):矩阵求行列式 A=[1,2;3,4]; det(A) ans=-2; inv(A):矩阵求逆 A=[1,2;3,4]; B=inv(A) B=[-2,1;1,5 ...
- matlab 解方程组
1.解方程 最近有多人问如何用matlab解方程组的问题,其实在matlab中解方程组还是很方便的,例如,对于代数方程组Ax=b(A为系数矩阵,非奇异)的求解,MATLAB中有两种方法:(1)x=in ...
- 【数学建模】MATLAB语法
一.向量.矩阵的表示和使用 format long %小数很多format short %默认4位小数format rat %显示最近的分数format short e %指数格式的数 尾数多少 e ...
- 【书单】matlab 科学计算、数值分析以及数学物理问题
1. 数学计算 MATLAB数值计算 MATLAB之父 : 编程实践 2. 数学物理问题 高等应用数学问题的MATLAB求解(第3版)(豆瓣评价极好) 3. 模式识别
随机推荐
- pyinstaller 打包工具的使用方法
pyinstaller的安装 下载后可以输入pip list查看是否安装成功 然后切换到项目的根目录输入 pyinstaller -i favicon.ico -w -c game.py -p Que ...
- spring AspectJ的Execution表达式(转载)
原文:http://blog.csdn.net/peng658890/article/details/7223046 在使用spring框架配置AOP的时候,不管是通过XML配置文件还是注解的方式都需 ...
- vue项目history模式下微信分享相关问题
import wx from '@/utils/wx' import { shareApi } from '@/api' // 微信验证 export function requireConfig() ...
- Java基础——面试、笔试
网址来源: http://www.nowcoder.com/discuss/5949?type=0&order=0&pos=4&page=2 参考资料:(java方面的一些面试 ...
- EXCL单元格公式——组装SQL用
="'"&F3&"'"
- 3D Computer Grapihcs Using OpenGL - 15 Draw Element Instanced
友情提示:继续本节之前,需要保存此前的代码,本节为了试验,会对代码做一些修改,但后续的修改需要我们把代码返回之前的进度. OpenGL内置支持Instancing,有专门的函数来处理这件事情. 为了方 ...
- yield return的使用。。。
因为要取两个集合不同的元素,所以写了个拓展方法,用到了yield这个关键字,然后就学习了一波.先上代码 public static IEnumerable<T> NoRetainAll&l ...
- [CSP-S模拟测试]:优化(贪心+DP)
题目描述 $visit\text{_}world$发现有下优化问题可以用很平凡的技巧解决,所以他给你分享了这样一道题:现在有长度为$N$的整数序列$\{ a_i\}$,你需要从中选出$K$个不想叫的连 ...
- localstorage sessionstorage cookie的区别
一.基本概念 Cookie cookie比较小,大小限制在4kb左右,是网景公司的前雇员 LouMontulli 在1993年3月的发明.它的主要用途有保存登录信息,比如你登录某个网站市场可以看到“记 ...
- [LeetCode]-algorithms-String to Integer (atoi)
Implement atoi to convert a string to an integer. Hint: Carefully consider all possible input cases. ...
