hiho #1502：最大子矩阵（元素和不超过k）

#1502 : 最大子矩阵

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

给定一个NxM的矩阵A和一个整数K，小Hi希望你能求出其中最大（元素数目最多）的子矩阵，并且该子矩阵中所有元素的和不超过K。

输入

第一行包含三个整数N、M和K。

以下N行每行包含M个整数，表示A。

对于40%的数据，1 <= N, M <= 10

对于100%的数据，1 <= N, M <= 250 1 <= K <= 2147483647 1 <= Aij <= 10000

输出

满足条件最大的子矩阵所包含的元素数目。如果没有子矩阵满足条件，输出-1。

样例输入

3 3 9
1 2 3
2 3 4
3 4 5

样例输出

4 

思路：

满足条件最大的子矩阵所包含的元素数目。如果没有子矩阵满足条件，输出-1。

与求最大子矩阵题目(hdu1559子矩阵的元素之和最大)方法类似。

设row[x][y]：第x行中前y个数的和

则row[x][q]-row[x][p]：第x行中第p+1~第q个数的和

行x~y列u~v的矩形的元素之和：row[x][v]-row[x][u-1]+row[x+1][v]-row[x+1][u-1]+…+row[y][v]-row[y][u-1]

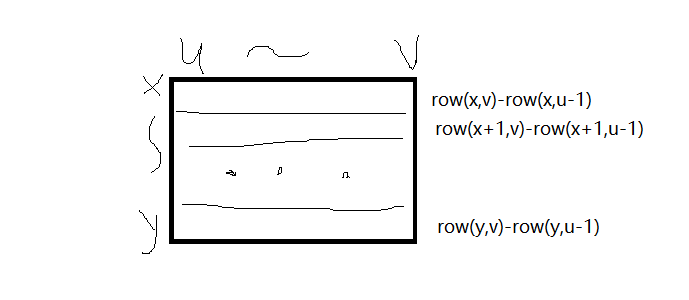
按照列固定：u~v (第u个数到第v个数)， 进行行的探索。

假设从行第p个数开始向下边2递增(每次p加1),假设到第q个数数值和第一次超过设定值，计算矩形面积(q-p)*(v-u+1)，

然后从第p个数开始向下边1递增(每次p+1)，直到数值和第一次小于设定值。

然后继续操作，直到v=n+1，结束。

代码：

 #include <iostream>
 #include <algorithm>
 using namespace std;

 int dp[][], a[][];
 int ans=-;
 int n,m,K;
 typedef long long LL;

 int main()
 {

     cin >> n>>m>>K;
     for (int i = ; i <= n; i++)
     {
         dp[i][]=;
         for (int j = ; j <= m; j++)
         {
             cin >> a[i][j];
             dp[i][j]=dp[i][j-]+a[i][j];
         }
     }

     for(int i=;i<=n;++i){
         for(int j=i;j<=n;++j){
             LL aa=;
             for(int k=,l=;k<=n;++k){
                 aa+=dp[k][j]-dp[k][i-];
                 while(aa>K){
                     aa-=dp[l][j]-dp[l][i-];
                     ++l;
                 }
                 ans=max(ans,(j-i+)*(k-l+));
             }
         }
     }

     cout << ans;
 }