图——图的Dijkstra法最短路径实现

1，最短路径的概念：

1，从有向图中某一顶点（起始顶点）到达另一顶点（终止顶点）的路径中，其权值之和最小的路径；

2，问题的提法：

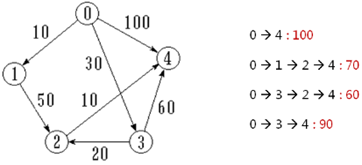
1，给定一个带权有向图 G 与起始顶点 v，求从 v 到 G 中其它顶点的最短路径（每条边上都存在有意义的权值）；

2，Dijkstra 算法核心是通过已知最短路径寻找未知最短路径；

3，解决思路：

1，Dijkstra 提出按路径长度的递增次序，逐步产生最短路径；

1，首先求出长度最短的一条最短路径，再参照它求出长度次短的一条最短路径，依次类推，直到从起始顶点 v 到其它各顶点的最短路径全部求出为止；

2，核心是通过递归的方式将从起始顶点到其他各顶点的最短路径全部求出来；

4，准备工作：

1，辅助数组：Array<E> dist；

1，dist[i] 表示当前从起始顶点 v0 到顶点 vi 的路径长度；

2，初始设置：

1，若从起始顶点 v0 到顶点 vi 有边：dist[i] 为该边上的权值；

2，若从起始顶点 v0 到顶点 vi 无边：dist[i] 为无穷大；

5，Dijkstra 算法演示：

1，由非空顶点集和边集这两个图的基本定义可知，集合在图的算法分析中的重要性，而集合在数据结构中常表现为数组；

2，每次关注的是刚刚加入 S 集合的顶点到其他顶点的连接，通过刚刚求得的最短路径值来求出抵达其他顶点的可能的最短路径值，这就是核心；

6，Dijkstra 算法步骤：

7，Dijkstra 算法精髓：

1，S 集合内的顶点是已经找到最短路径的顶点；

2，v0 到 w 的最短路径只能通过 S 集内的顶点；

3，dist[w] 可能改变：

8，如何记录最短路径上的各个顶点？

1，定义辅助数组：

1，Array<int> path；

1，path[i] 表示当前路径上的顶点 i 的前驱顶点；

2，初始化：path = {-1}；

3，修改：

9，Dijkstra 算法流程图：

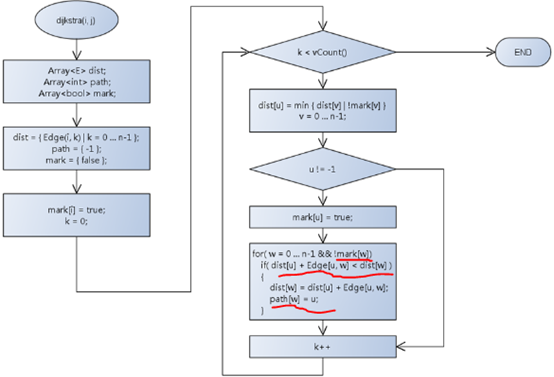
10，Dijkstra 最短路径算法：

 　　 /* 两个顶点之间最短路径，返回的数组表示两个最短路径上面的顶点 */
     SharedPointer< Array<int> > dijkstra(int i, int j, const E& LIMIT)  // O(n*n)
     {
         LinkQueue<int> ret;  // 保存最短路径上面的顶点

         if( ( <= i) && (i < vCount()) && ( <= j) && (j < vCount()) )
         {
             DynamicArray<E> dist(vCount());  // 用于存储路径值
             DynamicArray<int> path(vCount());  // 用于存储当前结点的前驱结点
             DynamicArray<bool> mark(vCount());  // 标记顶点是否进入 S 集合

             /* 原材料初始化 */
             for(int k=; k<vCount(); k++)
             {
                 mark[k] = false;  // 顶点都没在 S 集合中
                 path[k] = -;  // 路径没有顶点前驱

                 dist[k] = isAdjacent(i, k) ? (path[k]=i,getEdge(i, k)) : LIMIT;  // 如果初始结点和其他结点有连接，则设置为边上的权值，否则味无穷大；同时也要更新 path 数组，逗号表达式当前顶点 k 的前驱顶点是 i
             }

             mark[i] = true;  // 将起始顶点放入 S 集合中

             /* 大循环 */
             for(int k=; k<vCount(); k++)
             {
                 E m = LIMIT;
                 int u = -;

                 /* 遍历 dist 数组，从非S集合中找到到S 集合中顶点的最小路径值 */
                 for(int w=; w<vCount(); w++)
                 {
                     if( !mark[w] && (dist[w] < m) )  // 没有被标记的非 S 集中的点找最小值，更新小的值就是找最小路径值
                     {
                         m = dist[w];  // 找到了最小路径值
                         u = w;  // 最短路径记录的顶点
                     }
                 }

                 /* 判断是否有最小路径被找到，防止只有顶点没有边 */
                 if( u == - )
                 {
                     break;  // 只有顶点没有边，找不到两点间最短路径，因为此时 dist 数组都是理论最大值，找不到最小值，直接跳出
                 }

                 mark[u] = true;  // 在非 S 集中找到了顶点 u 对应的路径值是最小值，放入 S 集合

                 /* 算法核心：通过已知路径，推出 S 集合到非 S 集合顶点最短路径，由新加入的 u 来推动；这里的 w 是非 S 集合中的点，对其遍历；所有顶点都进入 S 集合中的时候，算法结束*/
                 for(int w=; w<vCount(); w++)
                 {
                     /* 以起始顶点 i 到 u 顶点的最短路径为基础，来计算通过已知最短路径所得到的到其它顶点路径是否最小，如果更小，则更新 dist 数组，这里的 w 是最小权值顶点 u 的邻接顶点，只要更小，就要更新 */
                     if( !mark[w] && isAdjacent(u, w) && (dist[u] + getEdge(u, w) < dist[w]) )
                     {
                         dist[w] = dist[u] + getEdge(u, w);
                         path[w] = u;  // 本次前驱顶点都是顶点 u 所代表的顶点
                     }
                 }
             }

             LinkStack<int> s;

             s.push(j);  // 终止顶点 j 先放入栈中；

             /* 将从起始顶点 i 到终值顶点 j 的点先放到栈中去；前驱结点的访问方式、值当做位置；值就是前面的顶点，所以直接把值压入进栈*/
             for(int k=path[j]; k!=-; k=path[k])
             {
                 s.push(k);
             }

             /* path 中保存的顶点顺序是逆序的，通过栈中转下，调整过来； */
             while( s.size() >  )
             {
                 ret.add(s.top());

                 s.pop();
             }
         }
         else
         {
             THROW_EXCEPTION(InvalidParameterException, "Index <i, j> is invalid ...");
         }

         /* 最终最短路径经历顶点数至少有 2 个，否则 i 到 j 是不可达的，最多多少顶点是不知道的 */
         if( ret.length() <  )
         {
             THROW_EXCEPTION(ArithmeticException, "There is no path from i to j ...");
         }

         return toArray(ret);  // 放到数组里面
     }

11，Dijkstra 最短路径算法测试代码：

 #include <iostream>
 #include "MatrixGraph.h"
 #include "ListGraph.h"

 using namespace std;
 using namespace DTLib;

 template< typename V, typename E >
 Graph<V, E>& GraphEasy()
 {
 　　 static MatrixGraph<, V, E> g;

     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
 　　 g.setEdge(, , );

     return g;
 }

 template< typename V, typename E >
 Graph<V, E>& GraphComplex()
 {
 　　 static ListGraph<V, E> g();

     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
 　　 g.setEdge(, , );

     return g;
 }

 int main()
 {
     Graph<int, int>& g = GraphComplex<int, int>();
 　　 SharedPointer< Array<int> > p = g.dijkstra(, , );

     for(int i=; i<p->length(); i++)
     {
         cout << (*p)[i] << " ";
 　　 }

 　　 cout << endl;

     return ;
 }

12，小结：

1，Dijkstra 最短路径算法是基于递推的思想完成的；

2，起始顶点到其他各顶点的最短路径通过动态推导得到；

3，未标记顶点的最短路径只能由已标记顶点计算得出；

4，算法的最终结果是起始顶点到其它各顶点的最短路径；