[CSP-S模拟测试]:w（树上DP）

题目背景

$\frac{1}{4}$遇到了一道水题，双完全不会做，于是去请教小$D$。小$D$看了${0.607}^2$眼就切掉了这题，嘲讽了$\frac{1}{4}$一番就离开了。于是，$\frac{1}{4}$只好来问你，这道题是这样的：

---

题目描述

有一棵$n$个节点的树，每条边长度为$1$，颜色为黑或白。
可以执行若干次如下操作：选择一条简单路径，反转路径上所有边的颜色。
对于某些边，要求在操作结束时为某一种颜色。
给定每条边的初始颜色，求最小操作数，以及满足操作数最小时，最小的操作路径长度和。

---

输入格式

从文件$w.in$中读入数据。
第一行，一个正整数$n$。
接下来$n−1$行，每行四个整数$a,b,c,d$：
$\bullet$树中有一条边连接$a$和$b$。
$\bullet c=0,1$表示初始颜色为白色、黑色。
$\bullet d=0,1,2$表示最终要求为白色、要求为黑色、没有要求。

---

输出格式

输出到文件$w.out$中。
输出一行，两个整数，表示最小操作数、操作数最小时的最小路径长度和。

---

样例

样例输入1：

5
2 1 1 0
1 3 0 1
2 4 1 2
5 2 1 1

样例输出1：

1 2

样例输入2：

3
1 3 1 2
2 1 0 0

样例输出2：

0 0

样例输入3：

6
1 3 0 1
1 2 0 2
2 4 1 0
4 5 1 0
5 6 0 2

样例输出3：

1 4

---

数据范围与提示

样例$1$解释：

操作路径$\{2,1,3\}$。

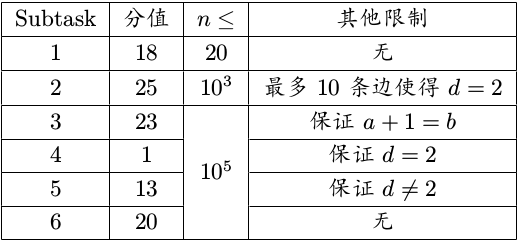
数据范围：

保证给出的图为一棵树，有$n\in [1,10^5],a,b\in [1,n],c\in \{0,1\},d\in\{0,1,2\}$。

---

题解

看到了这道题，我就像到了前一阵做过的一道题：虎。

然后我就死了……

那道题可以用贪心解决，但是这道题我们还需要回答最小的操作路径长度和……

不过有一些贪心策略还是可以利用一下的：

　　$\alpha.$每一条边不可能被翻转两次以上。

　　$\beta.$对于一个边集$E$，我们所需要翻转的次数为这个边集中奇数点的个数除$2$。

这道题要求我们在保证第一问最小的情况下尽可能保证第二问最小，所以这很难搞（居然连部分分都没有，伤心……）。

现在我们来考虑如何求出第二问，首先，定义$dp[i][0/1]$表示连接$i$的边是否翻转的最小代价（为方便，以下用二元组$pair<int,int>$分别表示第一问和第二问）。

现在考虑如何将儿子转移给父亲，设$w_1$表示已经转移的儿子中有一条与当前节点的连边翻转了的最小代价，$w_2$则表示还没有这样的一条边，则：

$$w_1=\min(w_1+dp[v][0],w_2+dp[v][1])$$

$$w_2=\min(w_1+dp[v][1],w_2+dp[v][0])$$

初始值：$w_1=(inf,inf),w_2=(0,0)$。

那么，现在我们已经求出了$w_1$和$w_2$，在来考虑如何更新$dp$中的答案。

这时候分两种情况：

　　$\alpha.$头顶的边一定要翻转：

$$dp[i][0]=(inf,inf)$$

$$dp[i][1]=\min((w1.first,w1.second+1),(w2.first+1,w2.second+1))$$

　　$\beta.$头顶的边不需要要翻转：

$$dp[i][0]=\min((w1.first+1,w1.second),w2)$$

$$dp[i][1]=(inf,inf)$$

最后的答案就是，第一问：$\dfrac{dp[i][0].first}{2}$；第二问：$dp[i][0].second$。

时间复杂度：$\Theta(n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
struct rec{int nxt,to,w;}e[200001];
int n;
int head[100001],cnt;
pair<int,int> dp[2][100001];
void add(int x,int y,int w)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	e[cnt].w=w;
	head[x]=cnt;
}
pair<int,int> pls(pair<int,int> a,pair<int,int> b){return make_pair(a.first+b.first,a.second+b.second);}
pair<int,int> min(pair<int,int> a,pair<int,int> b){return(a.first==b.first)?((a.second<b.second)?a:b):((a.first<b.first)?a:b);}
void dfs(int x,int fa,int w)
{
	pair<int,int> w1=make_pair(inf,inf);
	pair<int,int> w2=make_pair(0,0);
	for(int i=head[x];i;i=e[i].nxt)
		if(e[i].to!=fa)
		{
			dfs(e[i].to,x,e[i].w);
			pair<int,int> flag1=min(pls(w1,dp[0][e[i].to]),pls(w2,dp[1][e[i].to]));
			pair<int,int> flag2=min(pls(w1,dp[1][e[i].to]),pls(w2,dp[0][e[i].to]));
			w1=flag1;
			w2=flag2;
		}
	if(w==1)dp[0][x]=make_pair(inf,inf);
	else dp[0][x]=min(make_pair(w1.first+1,w1.second),w2);
	if(!w)dp[1][x]=make_pair(inf,inf);
	else dp[1][x]=min(make_pair(w1.first,w1.second+1),make_pair(w2.first+1,w2.second+1));
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;i++)
	{
		int a,b,c,d;
		scanf("%d%d%d%d",&a,&b,&c,&d);
		if(d==2){add(a,b,2);add(b,a,2);}
		else {add(a,b,c!=d);add(b,a,c!=d);}
	}
	dfs(1,0,2);
	printf("%d %d\n",dp[0][1].first>>1,dp[0][1].second);
	return 0;
}

---

rp++