如何将 不确定的有穷自动机(NFA) 转化为 确定的有穷自动机(DFA) 并将DFA最简化

一、从NFA到DFA的转换

例如下图：

DFA的每个状态都是一个由NFA中的状态构成的集合,即NFA状态集合的一个子集

r =aa*bb*cc*

二、从带有ε-边的NFA到DFA的转换

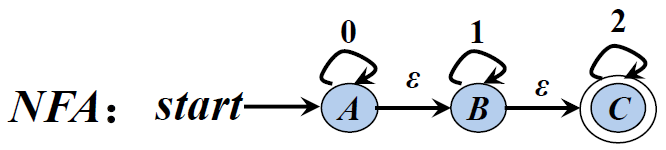
r=0*1*2*

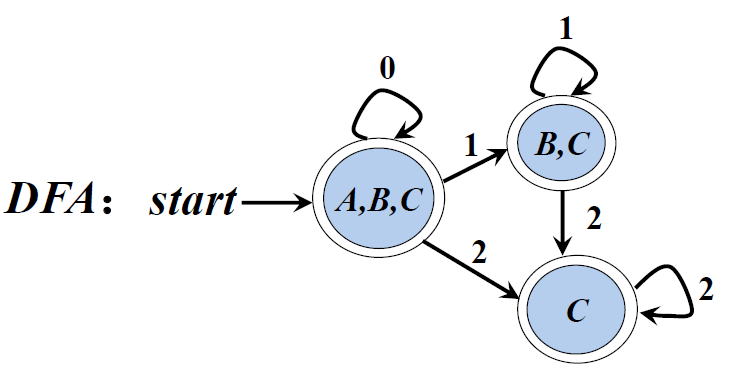
三、子集构造法（ subset construction）

 输入：NFA N
 输出：接收同样语言的DFA D
 方法：一开始，ε-closure （ s0 ）是Dstates 中的唯一状态，且它未加标记；

while（在Dstates中有一个未标记状态T ）
{
    给T加上标记；
    for（每个输入符号a）
    {
        U = ε-closure(move(T, a));
        if ( U不在Dstates中)
            将U加入到Dstates中，且不加标记；
        Dtran[T, a]=U ;
    }
} 

四、计算 ε-closure (T )

将T的所有状态压入stack中；将ε-closure  （T ）初始化为 T ；

 while(stack非空)
{
　　将栈顶元素 t 给弹出栈中；
　　for（每个满足如下条件的u ：从t出发有一个标号为ε的转换到达状态u)
 　　　　if ( u不在ε-closure  （T ）中）
　　　　{
　　　　　　将u加入到ε-closure  （T ）中；将u压入栈中;
　　　　}
}

接下来我们结合一个例题来具体实践一下根据正规文法构造NFA，接着确定化NFA，最后化简DFA

例：例题：为正规文法G[S]

S→aA|bQ

A→aA|bB|b

B→bD|aQ

Q→aQ|bD|b

D→bB|aA

E→aB|bF

F→bD|aE|b

构造相应的DFA。

答：

首先消除无用符号及其所在的产生式：
观察题目我们可以发现，E不出现在任何产生式的右部，所以E是无效符号，
删除E所在的产生式之后，符号F也不出现在任何产生式的右部，则F是无效符号，
删除F及其所在产生式。此时除了文法开始符号S之外，其余非终结符都是从S可达的。

 

接着便只需要为正规文法G[S]
       S→aA|bQ
       A→aA|bB|b
       B→bD|aQ
       Q→aQ|bD|b
       D→bB|aA
  构造相应的最简DFA。 

 

接着我们根据珍贵文法构造出下图的NFA：

 

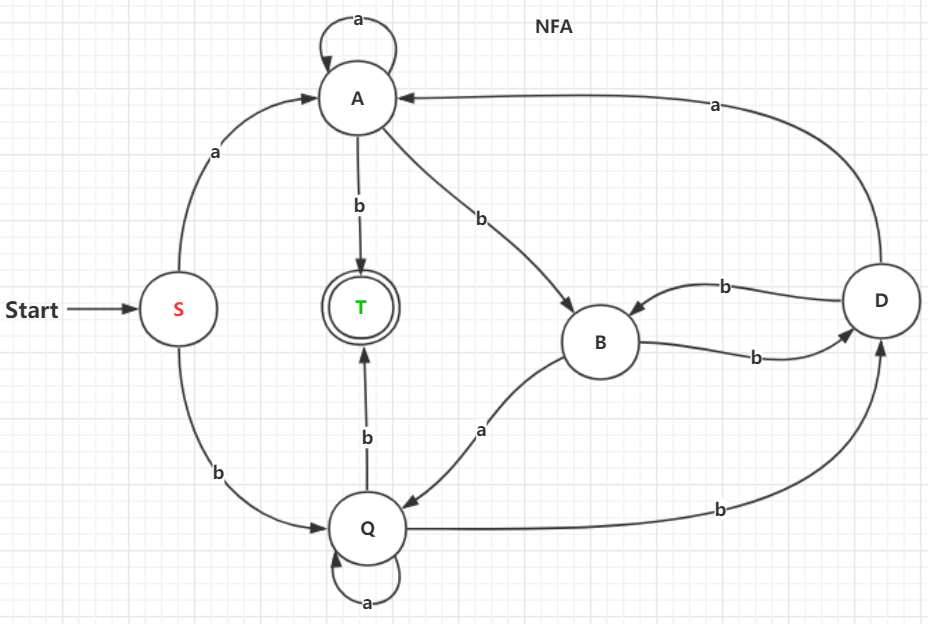
接下来我们将NFA进行确定化，新增一个状态T表示终止态：

构建下图的子集表，最开始只有起始态:

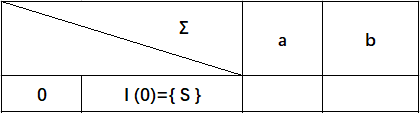
根据上图NFA，可得下图：

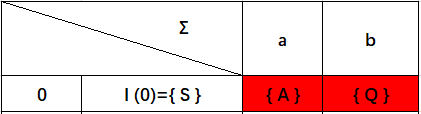
出现了两个新增状态子集{ A }{ Q}，我们把它加入到状态集中:

根据NFA可得出下表：

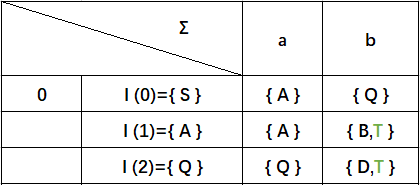
出现了两个新增状态子集{ B,T}{ D,T}(红色背景)，而{ A }{ Q}(绿色背景)已经存在与状态集中，可以不做处理。(字体颜色为绿色的T表示终态)，

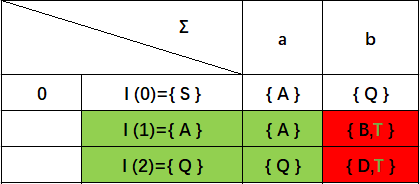
接着我们把新增的状态子集{ B,T}{ D,T}添加到状态集之中：

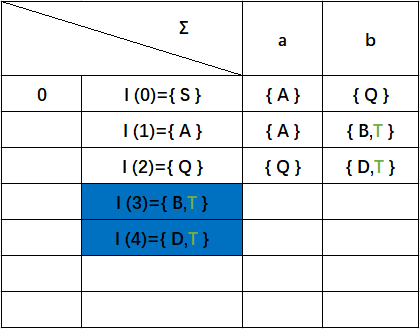
有NFA可得下表,可以根据上述方法看出，出现了新增状态子集{ B}{ D}(红色背景)，而{ A }{ Q}(绿色背景)已经存在与状态集中，可以不做处理。

接着我们把新增的状态子集{ B}{ D}添加到状态集之中

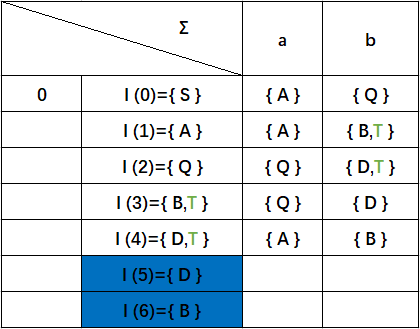
有NFA得出下表,发现已经没有新增的状态子集了：

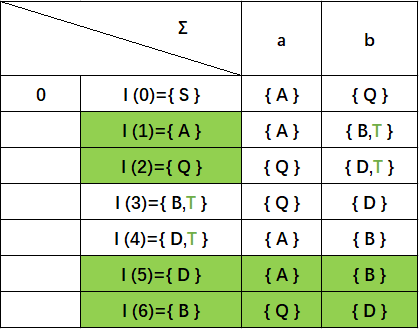
zhe这时候便可以重命名状态集，其中包含终态（绿色状态T）的子集相应的变成终态：

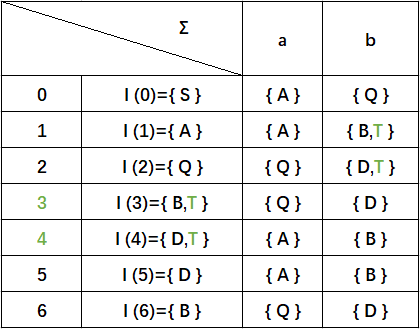
根据这个状态集表，我们构造DFA：

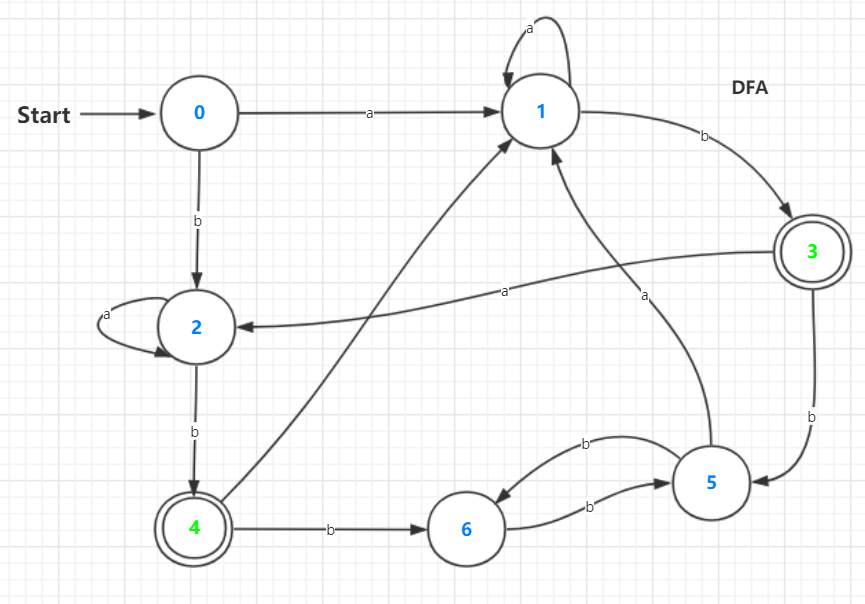
此时已经完成了NFA转化为DFA的过程，最后我们将DFA进行化简，这里采用的方法是“划分法”

首先我们将这留个状态划分为非终态集 { 0,1,2,5,6 }; 终态集 { 3,4 };

同样的我们首先将DFA的表简单直观的构造出来：

根据上表，可以得出如下图，

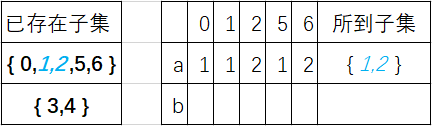
当非终态子集{ 0,1,2,5,6 }遇到a时,所得子集为{1,2}，包含于{ 0,1,2,5,6 }，暂时可以不用再分，转去考虑遇到b时的情况：

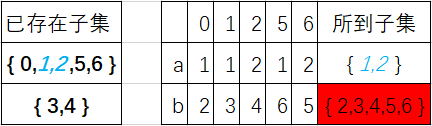
我们可以看到，经由b所得到的子集，不包含于任何一个已存在的子集，所以此时需要对非终态集 { 0,1,2,5,6 }进行划分，我们可以观察如下图：

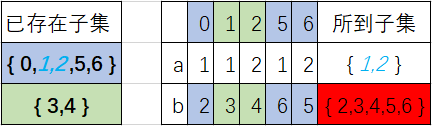
其中0,5,6三个状态经由b所得的子集是包含于已存在的子集{ 0,1,2,5,6 }中的，而状态1,2经由b所得的子集也是包含于已存在的子集{ 3 , 4}中的，所以我们再次划分为{0,5,6},{1,2}, { 3,4 }

这时候首先我们讨论子集{0,5,6}根据DFA表我们可以做出下表,经由a时的结果{1,2}包含于已存在子集：

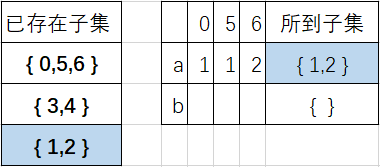
子集{0,5,6}根据DFA表，经由b时的结果{2,5,6}不包含于任何一个已存在子集：

观察下图：

我们发现需要将状态5,6再次分为一个子集，0单独分一个子集。得到新的已存在状态集:

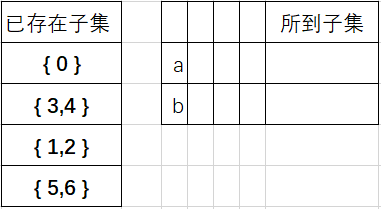
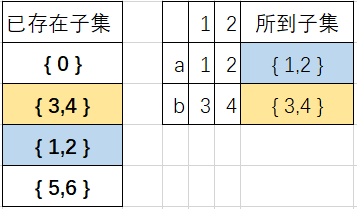
首先讨论子集{3,4},遇到a，b的情况，如下图;

所以此时子集{3,4}不需要再分。

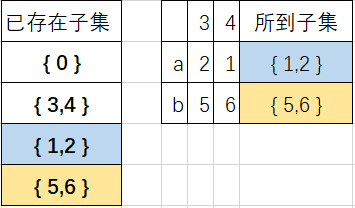
再讨论子集{1,2},遇到a，b的情况，如下图;

所以此时子集{1,2}也不需要再分。

再讨论子集{5,6},遇到a，b的情况，如下图;

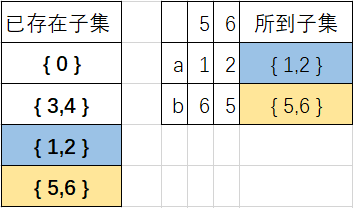
所以此时子集{5,6}也不需要再分.

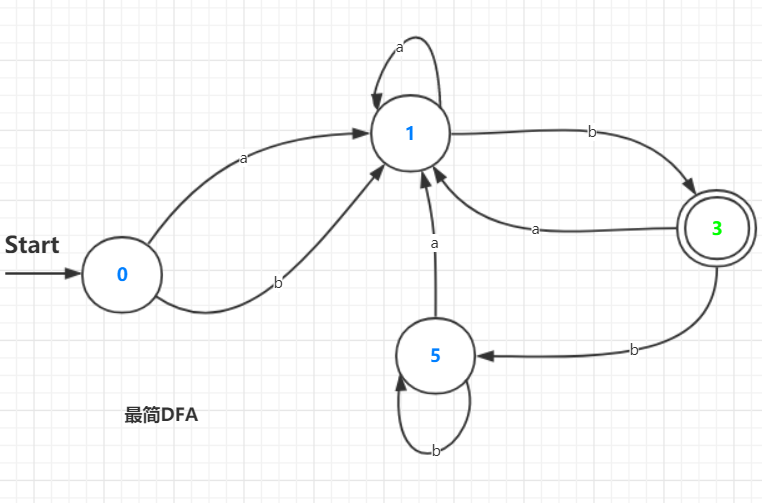
此时令状态3代表{3,4}（同时也是终态集），把原来到达状态4的弧都导入3，并删除状态4；

状态1代表{1,2}，把原来到达状态2的弧都导入1，并删除状态2；

状态5代表{5,6}，把原来到达状态6的弧都导入5，并删除状态6；

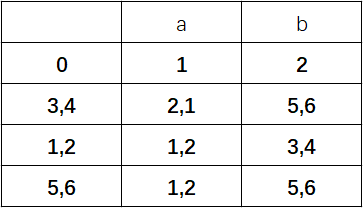
便得到了化简后的DFA：

结束