字符串匹配的Boyer-Moore算法 详解 加 C# 实现

上一篇文章，我介绍了KMP算法。

　　但是，它并不是效率最高的算法，实际采用并不多。各种文本编辑器的"查找"功能（Ctrl+F），大多采用Boyer-Moore算法。

　　Boyer-Moore算法不仅效率高，而且构思巧妙，容易理解。1977年，德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了这种算法。

　　下面，我根据Moore教授自己的例子来解释这种算法。

　　1.

　　假定字符串为"HERE IS A SIMPLE EXAMPLE"，搜索词为"EXAMPLE"。

　　2.

　　首先，"字符串"与"搜索词"头部对齐，从尾部开始比较。

　　这是一个很聪明的想法，因为如果尾部字符不匹配，那么只要一次比较，就可以知道前7个字符（整体上）肯定不是要找的结果。

　　我们看到，"S"与"E"不匹配。这时，"S"就被称为"坏字符"（bad character），即不匹配的字符。我们还发现，"S"不包含在搜索词"EXAMPLE"之中，这意味着可以把搜索词直接移到"S"的后一位。

　　3.

　　依然从尾部开始比较，发现"P"与"E"不匹配，所以"P"是"坏字符"。但是，"P"包含在搜索词"EXAMPLE"之中。所以，将搜索词后移两位，两个"P"对齐。

　　4.

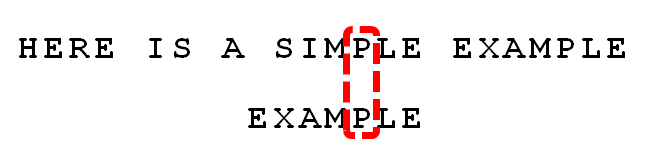
　　我们由此总结出"坏字符规则"：

　　后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置

　　如果"坏字符"不包含在搜索词之中，则上一次出现位置为 -1。

　　以"P"为例，它作为"坏字符"，出现在搜索词的第6位（从0开始编号），在搜索词中的上一次出现位置为4，所以后移 6 - 4 = 2位。再以前面第二步的"S"为例，它出现在第6位，上一次出现位置是 -1（即未出现），则整个搜索词后移 6 - (-1) = 7位。

　　5.

　　依然从尾部开始比较，"E"与"E"匹配。

　　6.

　　比较前面一位，"LE"与"LE"匹配。

　　7.

　　比较前面一位，"PLE"与"PLE"匹配。

　　8.

　　比较前面一位，"MPLE"与"MPLE"匹配。我们把这种情况称为"好后缀"（good suffix），即所有尾部匹配的字符串。注意，"MPLE"、"PLE"、"LE"、"E"都是好后缀。

　　9.

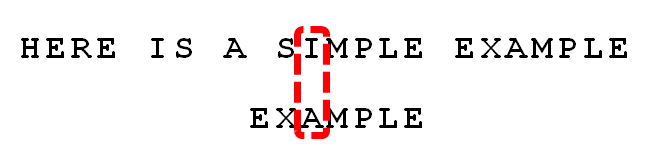
　　比较前一位，发现"I"与"A"不匹配。所以，"I"是"坏字符"。

　　10.

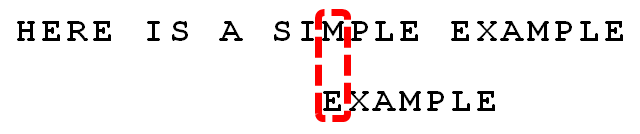
　　根据"坏字符规则"，此时搜索词应该后移 2 - （-1）= 3 位。问题是，此时有没有更好的移法？

　　11.

　　我们知道，此时存在"好后缀"。所以，可以采用"好后缀规则"：

　　后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置

　　举例来说，如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5（从0开始计算，取最后的"B"的值），在"搜索词中的上一次出现位置"是1（第一个"B"的位置），所以后移 5 - 1 = 4位，前一个"AB"移到后一个"AB"的位置。

　　再举一个例子，如果字符串"ABCDEF"的"EF"是好后缀，则"EF"的位置是5 ，上一次出现的位置是 -1（即未出现），所以后移 5 - (-1) = 6位，即整个字符串移到"F"的后一位。

　　这个规则有三个注意点：

　　（1）"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀，则它的位置以"F"为准，即5（从0开始计算）。

　　（2）如果"好后缀"在搜索词中只出现一次，则它的上一次出现位置为 -1。比如，"EF"在"ABCDEF"之中只出现一次，则它的上一次出现位置为-1（即未出现）。

　　（3）如果"好后缀"有多个，则除了最长的那个"好后缀"，其他"好后缀"的上一次出现位置必须在头部。比如，假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B"，请问这时"好后缀"的上一次出现位置是什么？回答是，此时采用的好后缀是"B"，它的上一次出现位置是头部，即第0位。这个规则也可以这样表达：如果最长的那个"好后缀"只出现一次，则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB"，即虚拟加入最前面的"DA"。

　　回到上文的这个例子。此时，所有的"好后缀"（MPLE、PLE、LE、E）之中，只有"E"在"EXAMPLE"还出现在头部，所以后移 6 - 0 = 6位。

　　12.

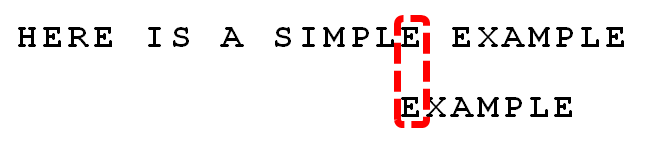
　　可以看到，"坏字符规则"只能移3位，"好后缀规则"可以移6位。所以，Boyer-Moore算法的基本思想是，每次后移这两个规则之中的较大值。

　　更巧妙的是，这两个规则的移动位数，只与搜索词有关，与原字符串无关。因此，可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时，只要查表比较一下就可以了。

　　13.

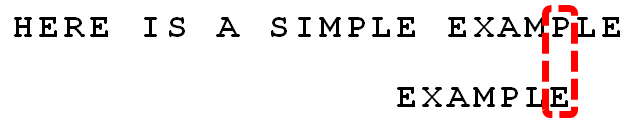
　　继续从尾部开始比较，"P"与"E"不匹配，因此"P"是"坏字符"。根据"坏字符规则"，后移 6 - 4 = 2位。

　　14.

　　从尾部开始逐位比较，发现全部匹配，于是搜索结束。如果还要继续查找（即找出全部匹配），则根据"好后缀规则"，后移 6 - 0 = 6位，即头部的"E"移到尾部的"E"的位置。

声明：BM算法的详解文章来阮一峰的博客，我这里没有侵权的意思，只是用来学习，望作者谅解！
     原文地址：
     http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html

下面是我用C#实现的上述算法：

         public static int Arithmetic_BM(string operateStr, string findStr)
         {
             //i：匹配开始的索引，j：operateStr字符串的索引迭代，k：findStr字符串索引迭代
             int i = , j = findStr.Length - , k = j;
             int n, m = ; //n:坏字符规则计算出的移动位数，m:好后缀计算出的移动位数

             while (k >=  && j < operateStr.Length)
             {
                 if (k == ) //全部匹配，return
                 {
                     return i;
                     break;
                 }
                 if (operateStr[j] == findStr[k]) //匹配，next
                 {
                     j--;
                     k--;
                 }
                 else
                 {
                     //当k<要匹配的字符串长度时，说明已经有匹配的字符了，即有“好后缀”
                     if (k < findStr.Length - )
                     {
                         //采用"好后缀规则"，先找出“全好后缀”有没有在前面存在
                         var goodSuffix = findStr.Substring(k + ); //分割出全好后缀
                         var tempStr = findStr.Substring(, k + ); //去掉好缀后的字符串
                         //最全好后缀在剩下的字符串中出现
                         if (tempStr.Contains(goodSuffix))
                         {
                             var lastGoodSuffix = char.Parse(goodSuffix.Substring(goodSuffix.Length - )); //好后缀的最后一个字符
                             //找出 该字符的出现位置
                             IList<int> indexs = new List<int>();
                             for (int x = ; x < tempStr.Length; x++)
                             {
                                 if (lastGoodSuffix == tempStr[x])
                                 {
                                     indexs.Add(x);
                                 }
                             }
                             //找出 好后缀在搜索词中的上一次出现位置
                             var result = -;
                             for (int x = indexs.Count - ; x >= ; x--)
                             {
                                 if (indexs[x] >= goodSuffix.Length &&
                                     tempStr.Substring(indexs[x] - goodSuffix.Length + , goodSuffix.Length) == goodSuffix)
                                 {
                                     result = indexs[x];
                                     break;
                                 }
                             }
                             //好后缀规则结果
                             m = findStr.Length -  - result;
                         }
                         //最长好后缀没有没出现，但是好后缀最后一个字符，出现在头部
                         //后移位数 = 好后缀的位置 - (0)搜索词中的上一次出现位置
                         else if (findStr.Substring(, ) == findStr.Substring(findStr.Length - ))
                         {
                             m = findStr.Length - ;
                         }
                         else //好后缀只出现一次  (后移位数 = 好后缀的位置 - (-1)搜索词中的上一次出现位置)
                         {
                             m = findStr.Length;
                         }
                     }
                     //坏字符规则：后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置
                     n = (j - i) - findStr.LastIndexOf(operateStr[j]);
                     //比较坏字符规则和好后缀规则移动的位数，得出最终移动位数
                     if (n > m)
                     {
                         i += n;
                         j = i + findStr.Length - ;
                     }
                     else
                     {
                         i += m;
                         j = i + findStr.Length - ;
                     }
                     k = findStr.Length - ;
                     m = ; //清零
                 }
             }
             return -;
         }

分享给大家，这是我自己写的不排除有问题，如有更好的实现，请提出。