建模算法(一)——线性规划
一、解决问题
主要是安排现有资源(一定),取得最好的效益的问题解决,而且约束条件都是线性的。
二、数学模型
1、一般数学模型
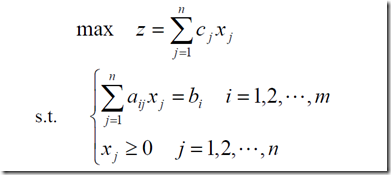
2、MATLAB数学模型
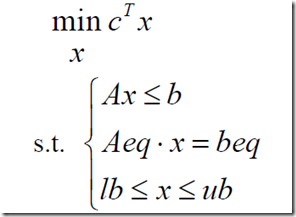
其中c,x都是列向量,A,Aeq是一个合适的矩阵,b,beq是合适的列向量。然后lb和ub是下限和上线(但是请注意= =,lb是一个变量的名字)
三、相关方程解法
1、图解法,画出可行域,这个可以进行编程进行实现、
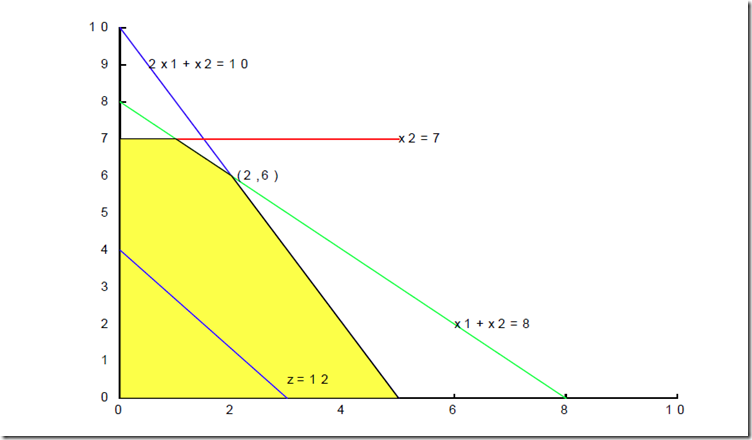
2、直接使用MATLAB的相关方法进行解题、
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,Xo,OPTIONS)
其中fval返回的是目标函数的值,然后x则是返回取到fval时x的对应的值,然后LB和UB是对应x的上界和下界(可以省略),x0是x的初始值(暂时可以忽略)
OPTIONS是控制参数。
四、一些其他问题转换成线性规划
1、绝对值之和最小
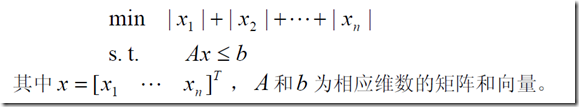
在这里我们就可以令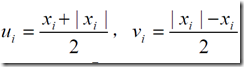 ,就可以满足
,就可以满足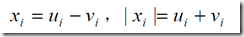 ,这样子这个问题就变成了
,这样子这个问题就变成了

2、两个数的差的绝对值,在xi固定时,取得max,之后在去定yi
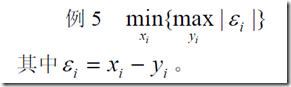
我们取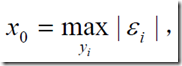 ,就可以转换问题了
,就可以转换问题了
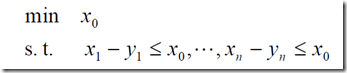
五、一些线性规划可以解决的实际问题
1、生产力有限,要求取得最大收益

2、运输问题(产销问题)
要求运输费用最小

在这里需要记得有一个很重要的等式,就是所有产地送出去的等于所有销售地收到的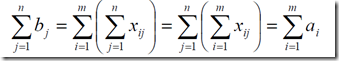
3、指派问题
要求花费的工作时间要最短

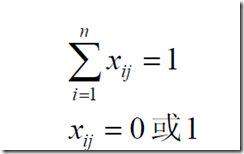
(2)求解指派问题的匈牙利算法、
首先我们要知道对与系数矩阵C由这样的性质,同时对每一行(列)加上或者减去同样的一个数,得到的新矩阵和原矩阵的指派问题具有相同的最优指派。
一般步骤是:
a、每行每列消除最小的数字,使得出现能够出现N(与矩阵大小相同)个位于不同行不同列的零元素,选定就是最优解。
b、如果上一步骤没办法直接完成,则、

4、对偶理论(与反函数相比较)
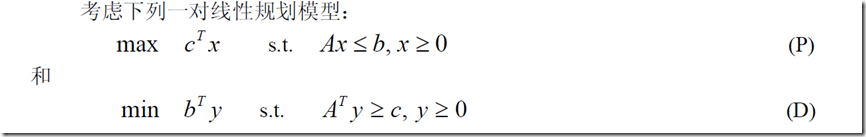

最重要的是掌握其性质,可以用来检验是不是最优解、、

5、投资的收益和风险(主要多目标函数如何并成一个目标函数)

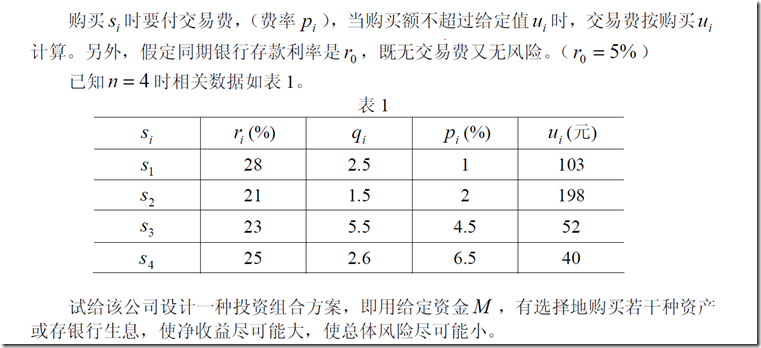
下一步主要是设立变量(这是数学建模中一步很关键的地方,你指标选的好,方程就好列好解,否则。。。。)

之后就是加入限定,一些理想化的假设

然后写出方程

其中第一个目标函数为收益,第二个为风险。
下一步就是化简目标函数
(1)固定风险水平,优化收益

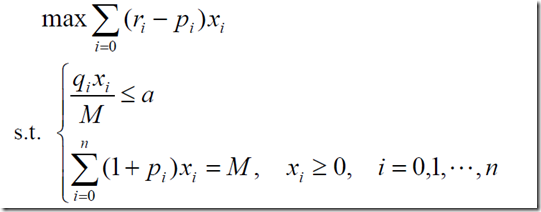
(2)固定盈利水平,极小化风险

(3)同时考虑两个,这样的话需要加入一个权重s。
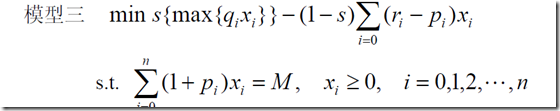
建模算法(一)——线性规划的更多相关文章
- Python小白的数学建模课-03.线性规划
线性规划是很多数模培训讲的第一个算法,算法很简单,思想很深刻. 要通过线性规划问题,理解如何学习数学建模.如何选择编程算法. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛 ...
- 建模算法(三)——非线性规划
一.非线性规划和线性规划不同之处 1.含有非线性的目标函数或者约束条件 2.如果最优解存在,线性规划只能存在可行域的边界上找到(一般还是在顶点处),而非线性规划的最优解可能存在于可行域的任意一点达到. ...
- 建模算法(二)——整数规划
一.概述 1.定义:规划中变量部分或全部定义成整数是,称为整数规划. 2.分类:纯整数规划和混合整数规划. 3.特点: (1)原线性规划有最优解,当自变量限制为整数后: a.原最优解全是整数,那最优解 ...
- python 版 mldivide matlab 反除(左除)《数学建模算法与程序》Python笔记
今天在阅读数学建模的时候看到了差分那章 其中有一个用matlab求线性的代码,这里我贴出来 这里我送上 Python代码 In [39]: import numpy as np ...: from s ...
- 建模算法(十一)——目标规划
求解多目标规划的思路 1.加权系数法 为每一个目标加一个权系数,把多目标模型转化成单一目标模型.但是困难时确定合理的权系数,以反映不同目标之间的重要程度. 2.优先等级法 将各目标按其重要程度分为不同 ...
- 建模算法(十)——灰色理论之关联度分析
一.数据变换技术 为了保证建模的质量和系统分析结果的准确性,对原始的数据要进行去量纲处理. 1.定义 设有序列,则成映射为序列x到序列y的数据变换. (1) f 是初值化变换. (2) f 是均值化变 ...
- 建模算法(六)——神经网络模型
(一)神经网络简介 主要是利用计算机的计算能力,对大量的样本进行拟合,最终得到一个我们想要的结果,结果通过0-1编码,这样就OK啦 (二)人工神经网络模型 一.基本单元的三个基本要素 1.一组连接(输 ...
- 建模算法(五)——图与网络
(一)图与网络的基本概念 一.无向图 含有的元素为顶点,弧和权重,但是没有方向 二.有向图 含有的元素为顶点,弧和权重,弧具有方向. 三.有限图.无限图 顶点和边有限就是有限图,否则就是无限图. 四. ...
- 【BZOJ1937】[Shoi2004]Mst 最小生成树 KM算法(线性规划)
[BZOJ1937][Shoi2004]Mst 最小生成树 Description Input 第一行为N.M,其中 表示顶点的数目, 表示边的数目.顶点的编号为1.2.3.…….N-1.N.接下来的 ...
随机推荐
- 使用qsort对结构体的数据排序
1007 DNA 排序 题目大意: 序列“未排序程度”的一个计算方式是元素乱序的元素对个数.例如:在单词序列“DAABEC'”中,因为D大于右边四个单词,E大于C,所以计算结果为5.这种计算方法称为序 ...
- fedora终端快捷键
在name框中填写这个快捷键的名称,比如open terminal(打开终端窗口) 在command框中填写执行这个快捷键的shell命令,此处可填写gnome-terminal
- C++ Primer Plus第6版18个重点笔记
下面是我看<C++ Primer Plus>第6版这本书后所做的笔记,作为备忘录便于以后复习. 笔记部分 C++的const比C语言#define更好的原因? 首先,它能够明确指定类型,有 ...
- ReactiveCocoa 和 MVVM 入门 (转)
翻译自ReactiveCocoa and MVVM, an Introduction. 文中引用的 Gist 可能无法显示.为了和谐社会, 请科学上网. MVC 任何一个正经开发过一阵子软件的人都熟悉 ...
- FFT(1)
FFT Complex struct complex{ double re,im; complex(double r,double i){re=r,im=i;} complex(){re=0.0,im ...
- editorial-render A
PROBLEM LINK: PracticeContest Author: adminTester: Kevin AtienzaEditorialist: Ajay K. VermaRussian T ...
- OpenResty(Nginx)+Lua+GraphicsMagick实现缩略图功能
http://www.hopesoft.org/blog/?p=1188 http://www.imagemagick.org/download/ 2.用法 原始图片是input.jpg,尺寸:160 ...
- php __set() __get() __isset() __unset()四个方法的应用
一般来说,总是把类的属性定义为private,这更符合现实的逻辑.但是,对属性的读取 和赋值操作是非常频繁的,因此在PHP5 中,预定义了两个函数“__get()”和“__set()”来获 取和赋值其 ...
- virsh常用命令
必须启动libvirtd,才能用virsh查看kvm后台. # systemctl start libvirtd 查看网络 # virsh net-list 启动default网络 # virsh n ...
- sharepoint更新多行文本webparth
前台 <script> function Copy() { var value = document.getElementById("<%=BodyBox.ClientID ...
