图的存储结构的实现(C/C++实现)
存档:
#include <stdio.h>
#include <stdlib.h>
#define maxv 10
#define max 10
typedef char elem;
typedef int elemtype;
#include "queue.h"
#include "mgraph.h"
void main()
{
mgraph g;
printf("1.初始化函数测试:\n");
initial(g);
printf("2.创建函数测试:\n");
create(g);
printf("3.输出函数测试:\n");
printg(g);
printf("4.输出顶点度函数测试:\n");
degree(g);
printf("5.深度优先遍历函数测试:\n");
dfstraverse(g);
printf("6.广度优先遍历函数测试:\n");
bfs(g);
}
//有向图的邻接矩阵,顶点数据为字符型
typedef struct MGraph
{
elem vexes[maxv];//顶点表
int edges[maxv][maxv];//邻接矩阵
int n,e;//顶点数n和边数e
}mgraph;
bool visited[maxv];//访问标志数组
void initial(mgraph &g)//初始化函数
{
int i,j;
g.e=;
g.n=;
for(j=;j<maxv;j++)
g.vexes[j]=;//建立顶点表
for(i=;i<maxv;i++)
{
for(j=;j<maxv;j++)
{
g.edges[i][j]=;//初始化邻接矩阵
}
}
}
int locate(mgraph g,elem u)//查找顶点对应的数组下标值
{
for(int i=;i<g.n;i++)
{
if(g.vexes[i]==u)
return i;
}
return -;
}
void create(mgraph &g)//创建图的邻接矩阵存储
{
int i,j,k;
elem u,v;
printf("请输入有向图的顶点数:");
scanf("%d",&g.n);
printf("请输入有向图的弧数:");
scanf("%d",&g.e);
fflush(stdin);//清空缓存中的数据
printf("请输入字符型顶点数据,如ABCD:");
for(j=;j<g.n;j++)
scanf("%c",&g.vexes[j]);//建立顶点表
fflush(stdin);
printf("请输入弧的信息,格式:弧尾,弧头\n");
for(k=;k<g.e;k++)
{
scanf("%c,%c",&u,&v);
i=locate(g,u);
j=locate(g,v);
g.edges[i][j]=;
fflush(stdin);
}
}
void printg(mgraph g)//输出有向图的邻接矩阵
{
int i,j;
printf("输入图的邻接矩阵存储信息:\n");
printf("顶点数据:\n");
for(i=;i<g.n;i++)
printf("%d:%c\n",i,g.vexes[i]);
printf("邻接矩阵数据:\n");
for(i=;i<g.n;i++)
{
for(j=;j<g.n;j++)
{
printf("%3d",g.edges[i][j]);
}
printf("\n");
}
}
void degree(mgraph g)//输出顶点的度
{
int i,j,in,out;
for(i=;i<g.n;i++)
{
in=;
out=;
for(j=;j<g.n;j++)
{
if(g.edges[i][j]!=)
out++;
if(g.edges[j][i]!=)
in++;
}
printf("顶点%c的出度为%d---入度为%d---度为%d\n",g.vexes[i],out,in,in+out);
}
}
int firstadjvex(mgraph g,int v)//顶点v的第一个邻接顶点
{
for(int i=;i<g.n;i++)
{
if(g.edges[v][i]==)
return i;
}
return -;
}
int nextadjvex(mgraph g,int v,int w)//顶点v的相对于w的下一个邻接顶点
{
for(int i=w+;i<g.n;i++)
{
if(g.edges[v][i]==)
return i;
}
return -;
}
void dfs(mgraph g,int v)//遍历一个连通分量
{
int w;
visited[v]=true;
printf("%c ",g.vexes[v]);
for(w=firstadjvex(g,v);w>=;w=nextadjvex(g,v,w))
{
if(!visited[w])
dfs(g,w);
}
}
void dfstraverse(mgraph g)//深度优先遍历
{
int v;
for(v=;v<g.n;v++)
visited[v]=false;//标志访问数组初始化
for(v=;v<g.n;v++)
{
if(!visited[v])
dfs(g,v);
}
}
void bfs(mgraph g)//广度优先遍历
{
int u=,v=,w=;
queue q;
for(v=;v<g.n;v++)
visited[v]=false;
initqueue(q);
for(v=;v<g.n;v++)
{
if(!visited[v])
{
visited[v]=true;
printf("%c ",g.vexes[v]);
enqueue(q,v);
while(!queueempty(q))
{
dequeue(q,u);
for(w=firstadjvex(g,u);w>=;w=nextadjvex(g,u,w))
{
if(!visited[w])
{
visited[w]=true;
printf("%c ",g.vexes[w]);
enqueue(q,w);
}
}
}
}
}
destroyqueue(q);
}
typedef struct
{
elemtype *base;//动态分配存储空间
int front;//头指针,若队列不空指向队列头元素
int rear;//尾指针,若队列不空指向队列尾元素的下一个位置
}queue;
void initqueue(queue &q)//初始化队列
{
q.base=new elemtype[max];//分配存储空间
if(!q.base)
{
printf("队列分配失败\n");
exit(-);
}
else
q.front=q.rear=;
}
int queueempty(queue q)//判断队列是否为空
{
if(q.front==q.rear)
return ;
else
return ;
}
void enqueue(queue &q,elemtype e)//入队列操作
{
if((q.rear+)%max==q.front)
{
printf("队满,无法插入新元素!\n");
exit(-);
}
else
{
q.base[q.rear]=e;
q.rear=(q.rear+)%max;
}
}
void dequeue(queue &q,elemtype e)//出队列操作
{
if(q.front==q.rear)//判断队列是否为空
{
printf("空队列,无法删除头元素!\n");
exit(-);
}
else
{
e=q.base[q.front];
q.front=(q.front+)%max;
}
}
void destroyqueue(queue &q)//销毁队列
{
free(q.base);
q.base=NULL;
q.front=;
q.rear=;
printf("\n");
}
运行结果如下:

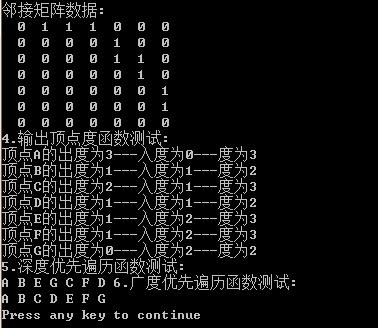
图的存储结构的实现(C/C++实现)的更多相关文章
- C++编程练习(9)----“图的存储结构以及图的遍历“(邻接矩阵、深度优先遍历、广度优先遍历)
图的存储结构 1)邻接矩阵 用两个数组来表示图,一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存储图中边或弧的信息. 2)邻接表 3)十字链表 4)邻接多重表 5)边集数组 本文只用代码实现用 ...
- K:图的存储结构
常用的图的存储结构主要有两种,一种是采用数组链表(邻接表)的方式,一种是采用邻接矩阵的方式.当然,图也可以采用十字链表或者边集数组的方式来进行表示,但由于不常用,为此,本博文不对其进行介绍. 邻接 ...
- 图的存储结构(邻接矩阵与邻接表)及其C++实现
一.图的定义 图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为: G=(V,E) 其中:G表示一个图,V是图G中顶点的集合,E是图G中顶点之间边的集合. 注: 在线性表中,元素个数可以为零, ...
- 【algo&ds】6.图及其存储结构、遍历
1.什么是图 图表示"多对多"的关系 包含 一组顶点:通常用 V(Vertex)表示顶点集合 一组边:通常用 E(Edge)表示边的集合 边是顶点对:(v,w)∈ E,其中 v,w ...
- 【PHP数据结构】图的存储结构
图的概念介绍得差不多了,大家可以消化消化再继续学习后面的内容.如果没有什么问题的话,我们就继续学习接下来的内容.当然,这还不是最麻烦的地方,因为今天我们只是介绍图的存储结构而已. 图的顺序存储结构:邻 ...
- 图的存储结构大赏------数据结构C语言(图)
图的存储结构大赏------数据结构C语言(图) 本次所讲的是常有的四种结构: 邻接矩阵 邻接表 十字链表 邻接多重表 邻接矩阵 概念 两个数组,一个表示顶点的信息,一个用来表示关联的关系. 如果是无 ...
- 图的存储结构与操作--C语言实现
图(graph)是一种比树结构还要复杂的数据结构,它的术语,存储方式,遍历方式,用途都比较广,所以如果想要一次性完成所有的代码,那代码会非常长.所以,我将分两次来完成图的代码.这一次,我会完成图的五种 ...
- 图的存储结构:邻接矩阵(邻接表)&链式前向星
[概念]疏松图&稠密图: 疏松图指,点连接的边不多的图,反之(点连接的边多)则为稠密图. Tips:邻接矩阵与邻接表相比,疏松图多用邻接表,稠密图多用邻接矩阵. 邻接矩阵: 开一个二维数组gr ...
- Search Quick Union Find(图的存储结构)
Quick Find:适用于search频繁的情况 每个节点有一个id值,id相同表示两个节点相连通.在union时要将等于某一个id值都改成另一个id值 Quick Union: 适用于union频 ...
随机推荐
- android JSON解析 fastjson和gson的使用
User user = new User(); user.setPhone("11111111"); user.setNmae("张三"); user.setP ...
- Android破解学习之路(四)——Android游戏 3D摩托飞车破解
经过前面三期的破解,想必大家已经非常熟悉破解的流程,这一篇也算是练手项目,我们继续来练习吧 apk下载地址:链接: https://pan.baidu.com/s/1sl3b3R3 密码: 6666 ...
- windos10安装mongodb并配置
想了想还是把这个写上吧,毕竟网上的教程有不少坑的. 首先下载mongodb,如果你嫌官网慢,那么你可以去我的百度云下载 链接:http://pan.baidu.com/s/1pKEWTBX 密码:v3 ...
- iOS----------如何检查域名是否支持ipv6
http://ipv6-test.com/validate.php 这个地址 也可以检测到! 1.检查你所用到的库,像af 3.0以上什么的(不用改),其他的库自己去搜下是否支持ipv6吧. 2. ...
- DeepLearning.ai学习笔记(三)结构化机器学习项目--week1 机器学习策略
一.为什么是ML策略 如上图示,假如我们在构建一个喵咪分类器,数据集就是上面几个图,训练之后准确率达到90%.虽然看起来挺高的,但是这显然并不具一般性,因为数据集太少了.那么此时可以想到的ML策略有哪 ...
- ExperDot的博客目录导航
最近活动 我更新了博客!粒子系统:从零开始画一棵树 Github:[ UWP ] [ JavaScript ] 自然编程 奇幻元纪 上帝创世篇:如何画一颗静态树 女娲补天篇:仿人工拼接碎片 吴刚伐桂 ...
- ArcGIS API for JavaScript 4.2学习笔记[11] 官方第五章Popups(弹窗)概览与解释
直接跳过第三第四章了,第三章Layer和第四章可视化,怎么说呢,Layer是组织数据的,是Map的属性之一.可视化属于符号化编程,暂时不看. 第五章是对数据.结果的显示,类似于alert()..NET ...
- .net 连接SqlServer数据库及基本增删改查
一.写在前面 因为这学期选修的 .net 课程就要上机考试了,所以总结下.net 操作 SqlServer 数据的方法.(因为本人方向是 Java,所以对.net 的了解不多,但以下所写代码均是经过测 ...
- Selinux安全机制
1.Selinux安全机制简介 Selinux是Google在Android 4.4上正式推出的一套以SELinux为基础于核心的系统安全机制.而SELinux则是由美国NSA(国安局)和一些公司(R ...
- lesson - 6 Linux下磁盘管理
1. 查看磁盘或者目录的容量df 查看磁盘各分区使用情况 不加参数以k为单位 df -i inode数,df -h 以G或者T或者M df -m 以M单位显示 du 查看目录或者文 ...
