“玲珑杯”ACM比赛 Round #12题解&源码
我能说我比较傻么！就只能做一道签到题，没办法，我就先写下A题的题解&源码吧，把官方给出的题解贴出来！
Time Limit：1s
Memory Limit：128MByte
DESCRIPTION
Niro, a lovely girl, has bought a Galaxy Note 7 and wants to destroy cities. There are N cities numbered 1... N on a line and each pair of adjacent cities has distance 1. Galaxy Note 7 has its explosion radius R. Niro puts her Galaxy Note 7 in city X and city i will be destroyed if (|X−i|≤R)
.You must tell Niro how many cities wil be destroyed.
Each of the following T lines contains three integers N, R, X.
OUTPUT
SAMPLE INPUT
0≤R≤100
1≤X≤N
#include <bits/stdc++.h>
using namespace std;
int main()
{
int T;
int n,r,x;
int a[];
while(scanf("%d",&T)!=EOF)
{
while(T--)
{
scanf("%d%d%d",&n,&r,&x);
memset(a,,sizeof(a));
int ans=;
if(x<=n)
{
for(int i=x;i<=x+r;i++)
{
if(i<=n)
{
a[i]=;
}
}
for(int i=x;i>=x-r;i--)
{
if(i>=)
{
a[i]=;
}
}
for(int i=;i<=n;i++)
if(a[i])
ans++;
printf("%d\n",ans);
}
}
}
return ;
}
给出官方的STL解法：
#include <cstdio>
#include <algorithm>
int T, N, R, X;
int main()
{
for (scanf("%d", &T); T--; )
{
scanf("%d%d%d", &N, &R, &X);
printf("%d\n", std::min(N, X + R) - std::max(, X - R) + );
}
return ;
}
题目链接：http://www.ifrog.cc/acm/problem/1107?contest=1014&no=1
题解：
下面给出AC代码：
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
const int INF = ;
class Heap
{
private :
std::priority_queue < int, std::vector < int >, std::greater < int > > inc, dec;
void BaseClear()
{
while (!dec.empty() && inc.top() == dec.top())
{
inc.pop();
dec.pop();
}
}
public :
int top()
{
BaseClear();
return inc.top();
}
void del(int x)
{
dec.push(x);
}
void push(int x)
{
inc.push(x);
}
void clear()
{
while (!inc.empty())
inc.pop();
while (!dec.empty())
dec.pop();
}
bool empty()
{
BaseClear();
return inc.empty();
}
}
Q0, Q1;
int TC, f0[], f1[], *F0 = f0 + , *F1 = f1 + , N, C0, C1, N0, N1, E0, E1, TAG0, TAG1;
void forward(char option)
{
if (option == '')
{
F0--;
F0[] = (Q1.empty() ? INF : Q1.top()) + TAG1 - TAG0;
E0++;
Q0.push(F0[]);
while (E0 >= N0)
Q0.del(F0[E0--]);
E1 = ;
Q1.clear();
}
else if (option == '')
{
F1--;
F1[] = (Q0.empty() ? INF : Q0.top()) + TAG0 - TAG1;
E1++;
Q1.push(F1[]);
while (E1 >= N1)
Q1.del(F1[E1--]);
E0 = ;
Q0.clear();
}
else
{
F0--;
F0[] = (Q1.empty() ? INF : Q1.top()) + TAG1 - TAG0;
E0++;
F1--;
F1[] = (Q0.empty() ? INF : Q0.top()) + TAG0 - TAG1;
E1++;
Q0.push(F0[]);
Q1.push(F1[]);
while (E0 >= N0)
Q0.del(F0[E0--]);
while (E1 >= N1)
Q1.del(F1[E1--]);
TAG0 += C0;
TAG1 += C1;
}
}
int main()
{
for (scanf("%d", &TC); TC--; )
{
F0 = f0 + ;
F1 = f1 + ;
TAG0 = TAG1 = ;
Q0.clear();
Q1.clear();
E0 = E1 = ;
scanf("%d%d%d%d%d", &N, &C0, &C1, &N0, &N1);
char c = getchar();
while (c != '' && c != '' && c != '?')
c = getchar();
if (c == '')
{
F0[E0 = ] = ;
Q0.push();
}
else if (c == '')
{
F1[E1 = ] = ;
Q1.push();
}
else
{
F0[E0 = ] = C0;
F1[E1 = ] = C1;
Q0.push(C0);
Q1.push(C1);
}
for (int i = ; i < N; i++)
forward(getchar());
int ans = ;
if (!Q0.empty())
ans = std::min(ans, Q0.top() + TAG0);
if (!Q1.empty())
ans = std::min(ans, Q1.top() + TAG1);
printf("%d\n", ans);
}
return ;
}
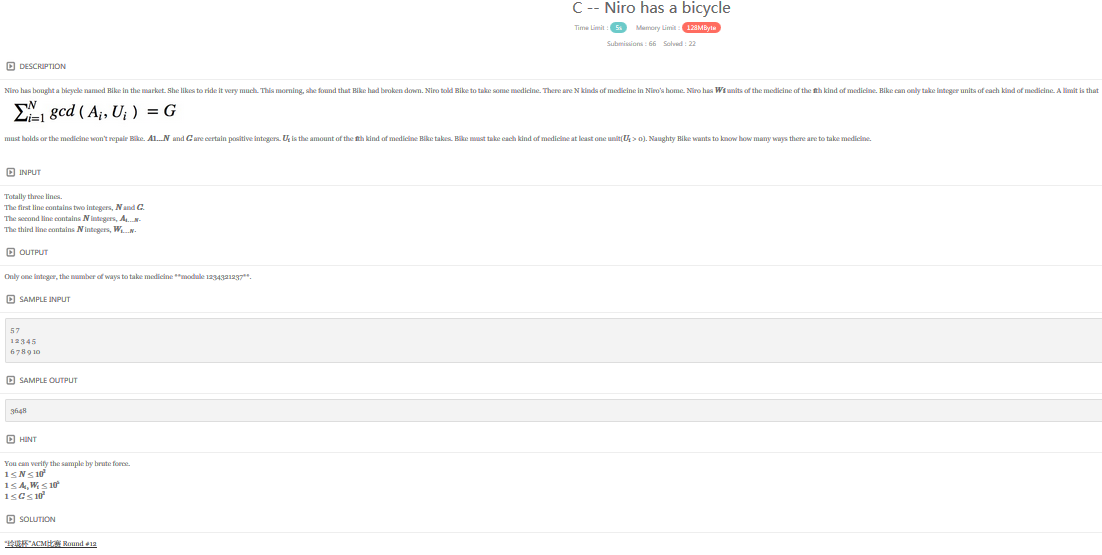
题目链接：http://www.ifrog.cc/acm/problem/1108?contest=1014&no=2
题解：
下面给出AC代码：
#include <bits/stdc++.h>
const int MOD = ;
int F[], N, G, a[], w[];
int gcd(int x, int y)
{
int r;
while (y)
{
r = x % y;
x = y;
y = r;
}
return x;
}
void DP(int x, int y)
{
std::vector < int > Div;
for (int i = ; i * i <= x; i++)
if (x % i == )
{
Div.push_back(i);
if (i * i < x)
Div.push_back(x / i);
}
std::sort(Div.begin(), Div.end());
int L = Div.size();
std::vector < int > Use(L, );
for (int i = L - ; ~i; i--)
{
Use[i] = y / Div[i];
for (int j = i + ; j < L; j++)
if (Div[j] % Div[i] == )
Use[i] -= Use[j];
}
for (int i = G; ~i; i--)
{
F[i] = ;
for (int j = ; j < L && Div[j] <= i; j++)
F[i] = (F[i] + (long long)F[i - Div[j]] * Use[j]) % MOD;
}
}
int main()
{
scanf("%d%d", &N, &G);
for (int i = ; i < N; i++)
scanf("%d", a + i);
for (int i = ; i < N; i++)
scanf("%d", w + i);
F[] = ;
for (int i = ; i < N; i++)
DP(a[i], w[i]);
printf("%d\n", F[G]);
return ;
}
题目链接：http://www.ifrog.cc/acm/problem/1109?contest=1014&no=3
题解：
下面给出AC代码：
#include <cstdio>
const long long MOD = ;
long long POWER(long long a, long long b)
{
long long r = ;
for (; b; b >>= )
{
if (b & )
r = r * a % MOD;
a = a * a % MOD;
}
return r;
}
long long N;
int T;
int main()
{
for (scanf("%d", &T); T--; )
{
scanf("%lld", &N);
long long F = POWER(, N - ) * - POWER(, N - ) * ;
long long G = POWER(, N - ) * (((N % MOD * ) - ) % MOD) + POWER(, N - ) * (((N % MOD * ) + ) % MOD);
G %= MOD;
F %= MOD;
G %= MOD;
F += MOD;
G += MOD;
F %= MOD;
G %= MOD;
if (G & )
G += MOD;
G >>= ;
printf("%lld %lld\n", F, G);
}
return ;
}
题目链接：http://www.ifrog.cc/acm/problem/1110?contest=1014&no=4
题解：
下面给出AC代码：
#include <cstdio>
#include <vector>
#include <algorithm>
std::vector < int > E[], col[];
std::vector < std::pair < int, int > > inc[], dec[];
int N, q[], left[], right[], size[], BeiZeng[][], *fa = BeiZeng[], LOG; // left : DFN; right maximum DFN in its subtree
std::vector < int >::iterator ue[];
void DFS()
{
int D = , TIME = ;
q[] = ;
ue[] = E[].begin();
left[] = right[] = ;
while (D)
{
if (ue[D] != E[q[D]].end() && *ue[D] == fa[q[D]])
ue[D]++;
if (ue[D] != E[q[D]].end())
{
int To = *ue[D]++;
fa[To] = q[D];
left[To] = right[To] = ++TIME;
q[++D] = To;
ue[D] = E[To].begin();
}
else
{
if (D > )
right[q[D - ]] = right[q[D]];
D--;
}
}
for (int i = ; i <= N; i++)
size[i] = right[i] - left[i] + ;
while ( << LOG < N)
LOG++;
for (int i = ; i <= LOG; i++)
for (int j = ; j <= N; j++)
BeiZeng[i][j] = BeiZeng[i - ][BeiZeng[i - ][j]];
}
int lowest(int u, int v)
{
for (int i = LOG; ~i; i--)
if (BeiZeng[i][u] && size[BeiZeng[i][u]] < size[v])
u = BeiZeng[i][u];
return u;
}
inline void bar(int u, int d, int l, int r)
{
inc[u].push_back(std::make_pair(l, r));
if (d < N)
dec[d + ].push_back(std::make_pair(l, r));
}
void conflict(int u, int v)
{
if (size[u] < size[v])
std::swap(u, v);
if (left[u] <= left[v] && right[v] <= right[u]) // u is v's ancestor
{
int lw = lowest(v, u);
if (left[lw] > )
{
bar(left[v], right[v], , left[lw] - );
bar(, left[lw] - , left[v], right[v]);
}
if (right[lw] < N)
{
bar(left[v], right[v], right[lw] + , N);
bar(right[lw] + , N, left[v], right[v]);
}
}
else
{
bar(left[u], right[u], left[v], right[v]);
bar(left[v], right[v], left[u], right[u]);
}
}
int MIN[], TAG[], NUM[]; // NUM[] : the number of elements which reach MIN[]
void INC(int p, int l, int r, int L, int R, int w)
{
if (L <= l && r <= R)
{
MIN[p] += w;
TAG[p] += w;
return;
}
if (TAG[p])
{
MIN[p + p] += TAG[p];
MIN[p + p + ] += TAG[p];
TAG[p + p] += TAG[p];
TAG[p + p + ] += TAG[p];
TAG[p] = ;
}
int m = (l + r) >> ;
if (L <= m)
INC(p + p, l, m, L, R, w);
if (R > m)
INC(p + p + , m + , r, L, R, w);
MIN[p] = std::min(MIN[p + p], MIN[p + p + ]);
NUM[p] = (MIN[p + p] == MIN[p] ? NUM[p + p] : ) + (MIN[p + p + ] == MIN[p] ? NUM[p + p + ] : );
}
inline int ZERONUM()
{
return MIN[] == ? NUM[] : ;
}
long long ANS;
void Treeinit(int p = , int l = , int r = N)
{
NUM[p] = r - l + ;
if (l < r)
{
int m = (l + r) >> ;
Treeinit(p + p, l, m);
Treeinit(p + p + , m + , r);
}
}
int main()
{
scanf("%d", &N);
for (int i = , u, v; i < N; i++)
{
scanf("%d%d", &u, &v);
E[u].push_back(v);
E[v].push_back(u);
}
for (int i = , c; i <= N; i++)
{
scanf("%d", &c);
col[c].push_back(i);
}
DFS();
for (int i = ; i <= N; i++)
for (std::vector < int >::iterator x = col[i].begin(); x != col[i].end(); x++)
for (std::vector < int >::iterator y = x + ; y != col[i].end(); y++)
conflict(*x, *y);
Treeinit();
for (int i = ; i <= N; i++)
{
for (std::vector < std::pair < int, int > >::iterator j = inc[i].begin(); j != inc[i].end(); j++)
INC(, , N, j -> first, j -> second, );
for (std::vector < std::pair < int, int > >::iterator j = dec[i].begin(); j != dec[i].end(); j++)
INC(, , N, j -> first, j -> second, -);
ANS += ZERONUM();
}
printf("%lld\n", (ANS - N) >> );
return ;
}
“玲珑杯”ACM比赛 Round #12题解&源码的更多相关文章
- “玲珑杯”ACM比赛 Round #19题解&源码【A,规律，B,二分，C,牛顿迭代法，D,平衡树，E,概率dp】
A -- simple math problem Time Limit:2s Memory Limit:128MByte Submissions:1599Solved:270 SAMPLE INPUT ...
- “玲珑杯”ACM比赛 Round #13 题解&源码
A 题目链接:http://www.ifrog.cc/acm/problem/1111 分析:容易发现本题就是排序不等式, 将A数组与B数组分别排序之后, 答案即N∑i=1Ai×Bi 此题有坑,反正据 ...
- “玲珑杯”ACM比赛 Round #1 题解
A:DESCRIPTION Eric has an array of integers a1,a2,...,ana1,a2,...,an. Every time, he can choose a co ...
- “玲珑杯”ACM比赛 Round #12 （D） 【矩阵快速幂的时间优化】
//首先,感谢Q巨 题目链接 定义状态向量b[6] b[0]:三面临红色的蓝色三角形个数 b[1]:两面临红色且一面临空的蓝色三角形个数 b[2]:一面临红色且两面临空的蓝色三角形个数 b[3]:三面 ...
- “玲珑杯”ACM比赛 Round #18
“玲珑杯”ACM比赛 Round #18 Start Time:2017-07-15 12:00:00 End Time:2017-07-15 15:46:00 A -- 计算几何你瞎暴力 Time ...
- “玲珑杯”ACM比赛 Round #19 B -- Buildings （RMQ + 二分）
“玲珑杯”ACM比赛 Round #19 Start Time:2017-07-29 14:00:00 End Time:2017-07-29 16:30:00 Refresh Time:2017-0 ...
- “玲珑杯”ACM比赛 Round #1
Start Time:2016-08-20 13:00:00 End Time:2016-08-20 18:00:00 Refresh Time:2017-11-12 19:51:52 Public ...
- “玲珑杯”ACM比赛 Round #18--最后你还是AK了（搜索+思维）
题目链接 DESCRIPTION INPUT OUTPUT SAMPLE INPUT 1 4 2 1 2 5 2 3 5 3 4 5 5 5 SAMPLE OUTPUT 35 HINT 对于样例, ...
- “玲珑杯”ACM比赛 Round #18---图论你先敲完模板（DP+思维）
题目链接 DESCRIPTION INPUT OUTPUT SAMPLE INPUT 2 3 2 3 5 7 3 10 3 5 7 SAMPLE OUTPUT 12 26 HINT 官方题解: 代码如 ...
随机推荐
- POJ2115(扩展欧几里得)
C Looooops Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 23700 Accepted: 6550 Descr ...
- android：在ViewPager中使用Button
最近在项目用用到ViewPager ,其中页面包含有Button,因为之前也有使用个ViewPager ,所以这个也照搬之前的方式,测试后发现点击button无法执行,这个button是在第一页面的默 ...
- block和delegate的区别
代理 可读性高 大部分可以属性 block 写的代码少 一般作为参数通知 占用资源 无论是block还是delegate模式本质上都是回调,使用block,其优点是回调的block代码块直 ...
- Java语言开发环境搭建
在使用任何计算机语言开发之前,都要搭建其开发环境. 一.明确什么是JDK.JRE. 二.下载JDK 三.安装JDK 四.配置环境变量 五.验证是否成功 一.什么是JRE.JDK. JRE(Java R ...
- 【转】IntelliJ IDEA2016.1 + maven 创建java web 项目
最近开始使用idea 来写java项目了,这个很流行,相比Eclipse方便了很多.功能多了,相对应的使用的复杂度也较高了,因为网上很多的使用和创建项目的简单教程,都是基于老版本的,每个新版本都有不一 ...
- 为什么使用enable_shared_from_this——shared_ptr两类错误
在使用C++实现弱回调时,订阅者应当维护一系列发布者的weak_ptr,而发布者注册回调时要传出this的shared_ptr指针,流行的实现方法是使用std::enable_shared_from_ ...
- 杭电2000——ASCII码排序
/* ASCII码排序 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Tota ...
- Java编程风格学习（三）
在上一篇的java编程风格学习(二)中我们学习了一些在Java编码过程中的格式规范,遵循这些规范毋庸置疑是我们的书写高质量代码的前提与基础.今天我们更进一步,一起来学习Java编程的命名规范,向着编写 ...
- 小红帽5.9 配置静态IP上网问题
本来无一物,何处染尘埃. DHCP连得好好的,手痒试下STATIC,静态IP 首先进入/etc/sysconfig/network-scripts/ifcfg-eth0, 写入各种参数: BOOTPR ...
- HTML文档及标签介绍
HTML标签 HTML 标记标签通常被称为 HTML 标签 (HTML tag). HTML标签是由尖括号包含的关键词,比如<html> HTML标签通常是成对出现的,比如<body ...