【机器学习】代价函数（cost function）

注：代价函数（有的地方也叫损失函数，Loss Function）在机器学习中的每一种算法中都很重要，因为训练模型的过程就是优化代价函数的过程，代价函数对每个参数的偏导数就是梯度下降中提到的梯度，防止过拟合时添加的正则化项也是加在代价函数后面的。在学习相关算法的过程中，对代价函数的理解也在不断的加深，在此做一个小结。

1. 什么是代价函数？

---

假设有训练样本(x, y)，模型为h，参数为θ。h(θ) = θ^Tx（θ^T表示θ的转置）。

（1）概况来讲，任何能够衡量模型预测出来的值h(θ)与真实值y之间的差异的函数都可以叫做代价函数C(θ)，如果有多个样本，则可以将所有代价函数的取值求均值，记做J(θ)。因此很容易就可以得出以下关于代价函数的性质：

• 对于每种算法来说，代价函数不是唯一的；
• 代价函数是参数θ的函数；
• 总的代价函数J(θ)可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本(x, y)；
• J(θ)是一个标量；

（2）当我们确定了模型h，后面做的所有事情就是训练模型的参数θ。那么什么时候模型的训练才能结束呢？这时候也涉及到代价函数，由于代价函数是用来衡量模型好坏的，我们的目标当然是得到最好的模型（也就是最符合训练样本(x, y)的模型）。因此训练参数的过程就是不断改变θ，从而得到更小的J(θ)的过程。理想情况下，当我们取到代价函数J的最小值时，就得到了最优的参数θ，记为：

$$\displaystyle \min_{ \theta } J(\theta)$$

例如，J(θ) = 0，表示我们的模型完美的拟合了观察的数据，没有任何误差。

（3）在优化参数θ的过程中，最常用的方法是梯度下降，这里的梯度就是代价函数J(θ)对θ₁, θ₂, ..., θ_n的偏导数。由于需要求偏导，我们可以得到另一个关于代价函数的性质：

• 选择代价函数时，最好挑选对参数θ可微的函数（全微分存在，偏导数一定存在）

2. 代价函数的常见形式

---

经过上面的描述，一个好的代价函数需要满足两个最基本的要求：能够评价模型的准确性，对参数θ可微。

2.1 均方误差

在线性回归中，最常用的是均方误差(Mean squared error)，具体形式为：

$$J(\theta_0, \theta_1) = \frac{ 1 }{ 2m } \displaystyle \sum_{ i = 1 }^{ m } (\hat{ y }^{(i)} - y^{(i)})^2 = \frac{ 1 }{ 2m } \displaystyle \sum_{ i = 1 }^{ m } (h_\theta(x^{(i)}) - y^{(i)})^2 $$

m：训练样本的个数；

h_θ(x)：用参数θ和x预测出来的y值；

y：原训练样本中的y值，也就是标准答案

上角标(i)：第i个样本

2.2 交叉熵

在逻辑回归中，最常用的是代价函数是交叉熵(Cross Entropy)，交叉熵是一个常见的代价函数，在神经网络中也会用到。下面是《神经网络与深度学习》一书对交叉熵的解释：

交叉熵是对「出乎意料」（译者注：原文使用suprise）的度量。神经元的目标是去计算函数y, 且y=y(x)。但是我们让它取而代之计算函数a, 且a=a(x)。假设我们把a当作y等于1的概率，1−a是y等于0的概率。那么，交叉熵衡量的是我们在知道y的真实值时的平均「出乎意料」程度。当输出是我们期望的值，我们的「出乎意料」程度比较低；当输出不是我们期望的，我们的「出乎意料」程度就比较高。

在1948年，克劳德·艾尔伍德·香农将热力学的熵，引入到信息论，因此它又被称为香农熵(Shannon Entropy)，它是香农信息量(Shannon Information Content, SIC)的期望。香农信息量用来度量不确定性的大小：一个事件的香农信息量等于0，表示该事件的发生不会给我们提供任何新的信息，例如确定性的事件，发生的概率是1，发生了也不会引起任何惊讶；当不可能事件发生时，香农信息量为无穷大，这表示给我们提供了无穷多的新信息，并且使我们无限的惊讶。更多解释可以看这里。

$$J(\theta) = -\frac{ 1 }{ m }[\sum_{ i=1 }^{ m } ({y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)})})]$$

符号说明同上

2.3 神经网络中的代价函数

学习过神经网络后，发现逻辑回归其实是神经网络的一种特例（没有隐藏层的神经网络）。因此神经网络中的代价函数与逻辑回归中的代价函数非常相似：

$$J(\theta) = -\frac{ 1 }{ m }[\sum_{ i=1 }^{ m } \sum_{ k=1 }^{ K } ({y_k^{(i)} \log h_\theta(x^{(i)}) + (1 - y_k^{(i)}) \log (1 - (h_\theta(x^{(i)}))_k})]$$

这里之所以多了一层求和项，是因为神经网络的输出一般都不是单一的值，K表示在多分类中的类型数。

例如在数字识别中，K=10，表示分了10类。此时对于某一个样本来说，输出的结果如下：

  1.1266e-004
  1.7413e-003
  2.5270e-003
  1.8403e-005
  9.3626e-003
  3.9927e-003
  5.5152e-003
  4.0147e-004
  6.4807e-003
  9.9573e-001

一个10维的列向量，预测的结果表示输入的数字是0~9中的某一个的概率，概率最大的就被当做是预测结果。例如上面的预测结果是9。理想情况下的预测结果应该如下（9的概率是1，其他都是0）：

   0
   0
   0
   0
   0
   0
   0
   0
   0
   1

比较预测结果和理想情况下的结果，可以看到这两个向量的对应元素之间都存在差异，共有10组，这里的10就表示代价函数里的K，相当于把每一种类型的差异都累加起来了。

3. 代价函数与参数

---

代价函数衡量的是模型预测值h(θ) 与标准答案y之间的差异，所以总的代价函数J是h(θ)和y的函数，即J=f(h(θ), y)。又因为y都是训练样本中给定的，h(θ)由θ决定，所以，最终还是模型参数θ的改变导致了J的改变。对于不同的θ，对应不同的预测值h(θ)，也就对应着不同的代价函数J的取值。变化过程为：

$$\theta --> h(\theta) --> J(\theta)$$

θ引起了h(θ)的改变，进而改变了J(θ)的取值。为了更直观的看到参数对代价函数的影响，举个简单的例子：

有训练样本{(0, 0), (1, 1), (2, 2), (4, 4)}，即4对训练样本，每个样本对中第1个数表示x的值，第2个数表示y的值。这几个点很明显都是y=x这条直线上的点。如下图：

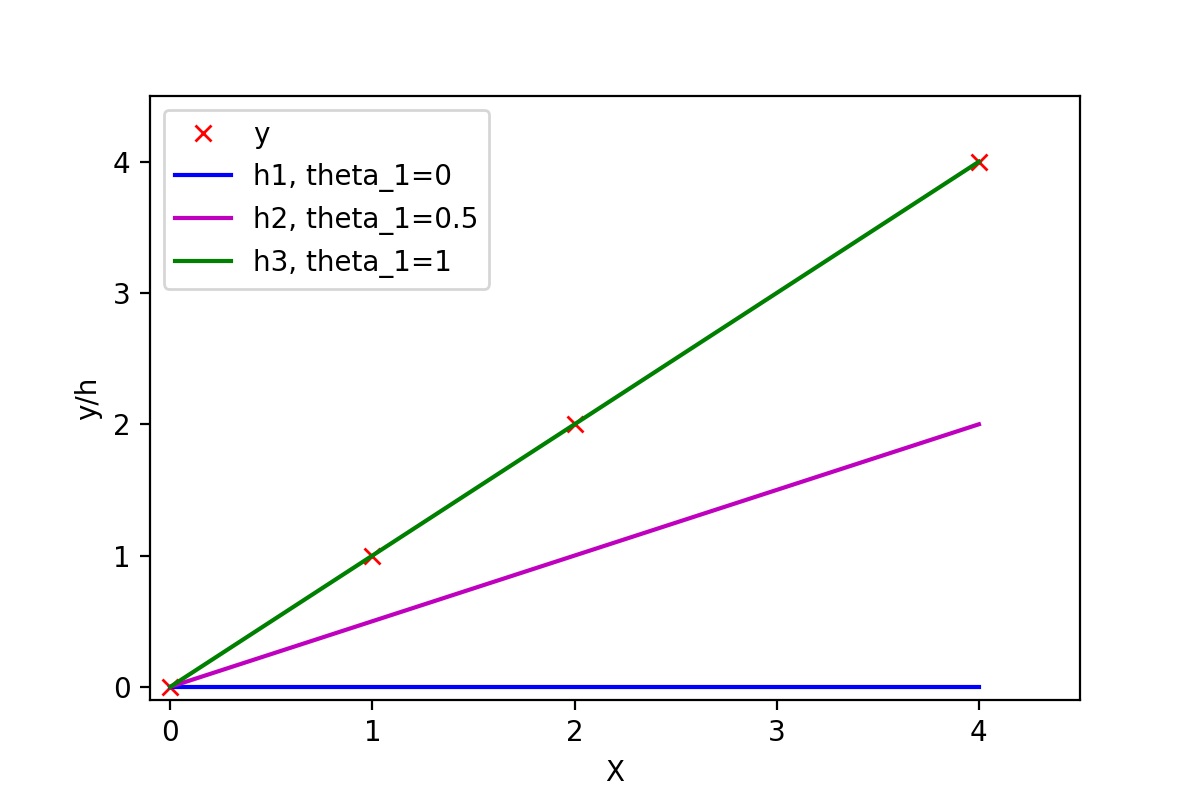
图1：不同参数可以拟合出不同的直线

"""
Spyder Editor

Python 3.6, Belter, 20170401
"""

import matplotlib.pyplot as plt
import numpy as np
X = np.array([[0, 1, 2, 4]]).T  # 都转换成列向量
y = np.array([[0, 1, 2, 4]]).T
theta1 = np.array([[0, 0]]).T  # 三个不同的theta_1值
theta2 = np.array([[0, 0.5]]).T
theta3 = np.array([[0, 1]]).T
X_size = X.shape
X_0 = np.ones((X_size[0],1))  # 添加x_0
X_with_x0 = np.concatenate((X_0, X), axis=1)
h1 = np.dot(X_with_x0, theta1)
h2 = np.dot(X_with_x0, theta2)
h3 = np.dot(X_with_x0, theta3)
plt.plot(X, y, 'rx', label='y')
plt.plot(X, h1, 'b', label='h1, theta_1=0')
plt.plot(X, h2, 'm', label='h2, theta_1=0.5')
plt.plot(X, h3, 'g', label='h3, theta_1=1')
plt.xlabel('X')
plt.ylabel('y/h')
plt.axis([-0.1, 4.5, -0.1, 4.5])
plt.legend(loc='upper left')
plt.savefig('liner_gression_error.png', dpi=200)

常数项为0，所以可以取θ₀=0，然后取不同的θ₁，可以得到不同的拟合直线。当θ₁=0时，拟合的直线是y=0，即蓝色线段，此时距离样本点最远，代价函数的值（误差）也最大；当θ₁=1时，拟合的直线是y=x，即绿色线段，此时拟合的直线经过每一个样本点，代价函数的值为0。

通过下图可以查看随着θ₁的变化，J(θ)的变化情况：

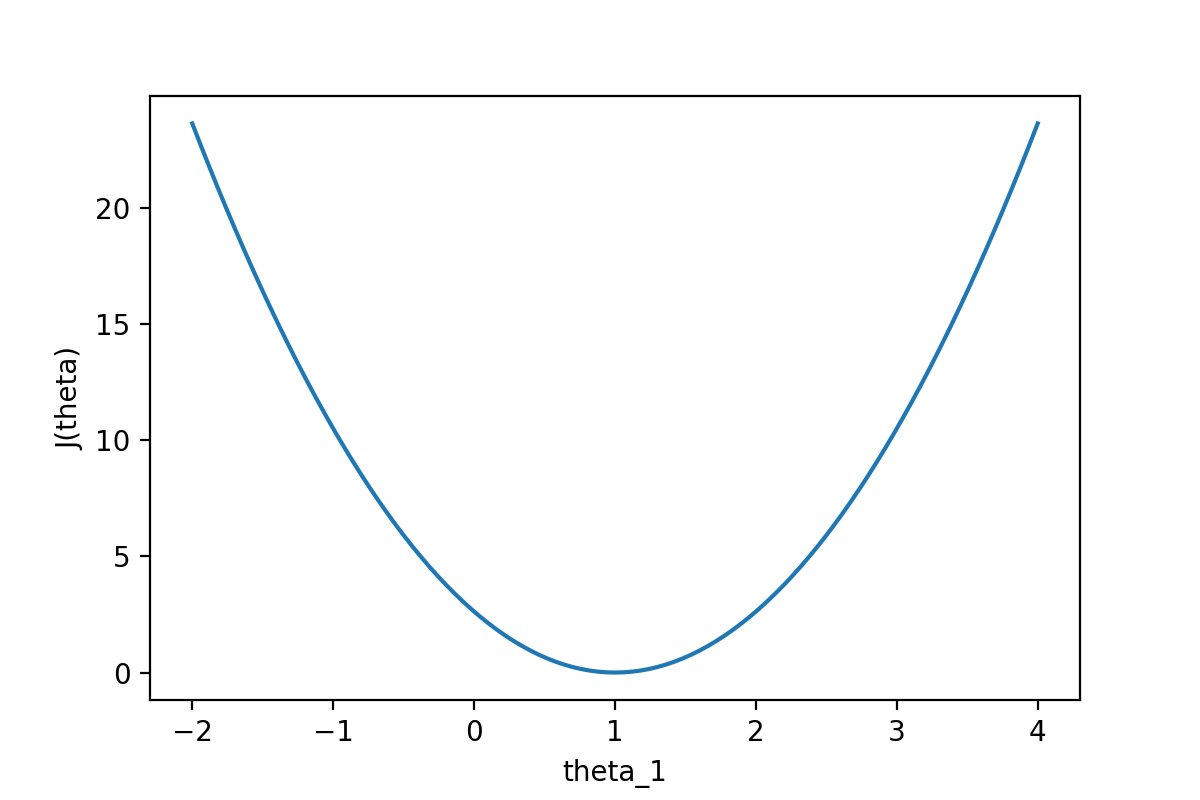
图2：代价函数J(θ)随参数的变化而变化

"""
Spyder Editor

Python 3.6, Belter, 20170401
"""

# 计算代价函数的值
def calcu_cost(theta, X, y):
    m = X.shape[0]  # sample size
    X_0 = np.ones((m,1))
    X_with_x0 = np.concatenate((X_0, X), axis=1)
    h = np.dot(X_with_x0, theta)
    return(np.dot((h-y).T, (h-y))/(2*m))

X = np.array([[0, 1, 2, 4]]).T
y = np.array([[0, 1, 2, 4]]).T
theta_0 = np.zeros((101, 1))
theta_1 = np.array([np.linspace(-2, 4, 101)]).T
theta = np.concatenate((theta_0, theta_1), axis=1)  # 101组不同的参数
J_list = []
for i in range(101):
    current_theta = theta[i:i+1].T
    cost = calcu_cost(current_theta, X, y)
    J_list.append(cost[0,0])
plt.plot(theta_1, J_list)
plt.xlabel('theta_1')
plt.ylabel('J(theta)')
plt.savefig('cost_theta.png', dpi=200)

从图中可以很直观的看到θ对代价函数的影响，当θ₁=1时，代价函数J(θ)取到最小值。因为线性回归模型的代价函数（均方误差）的性质非常好，因此也可以直接使用代数的方法，求J(θ)的一阶导数为0的点，就可以直接求出最优的θ值（正规方程法）。

4. 代价函数与梯度

---

梯度下降中的梯度指的是代价函数对各个参数的偏导数，偏导数的方向决定了在学习过程中参数下降的方向，学习率（通常用α表示）决定了每步变化的步长，有了导数和学习率就可以使用梯度下降算法（Gradient Descent Algorithm）更新参数了。下图中展示了只有两个参数的模型运用梯度下降算法的过程。

下图可以看做是代价函数J(θ)与参数θ做出的图，曲面上的一个点(θ₀, θ₁, J(θ))，有无数条切线，在这些切线中与x-y平面(底面，相当于θ₀, θ₁)夹角最大的那条切线就是该点梯度的方向，沿该方向移动，会产生最大的高度变化(相对于z轴，这里的z轴相当于代价函数J(θ))。

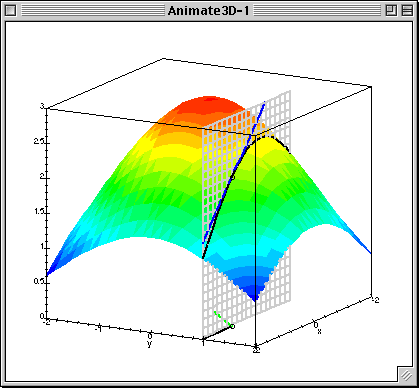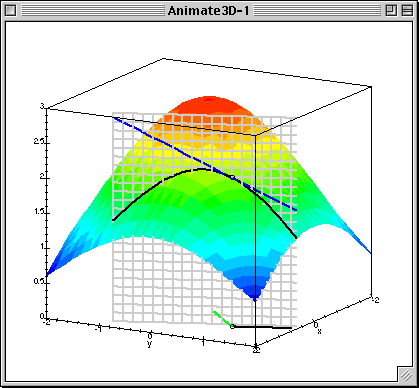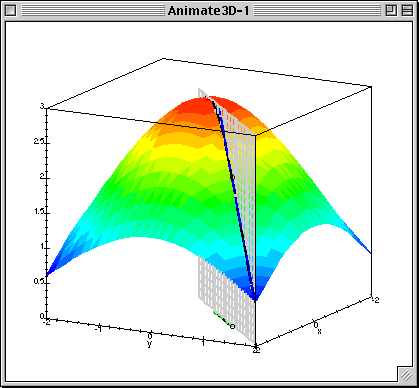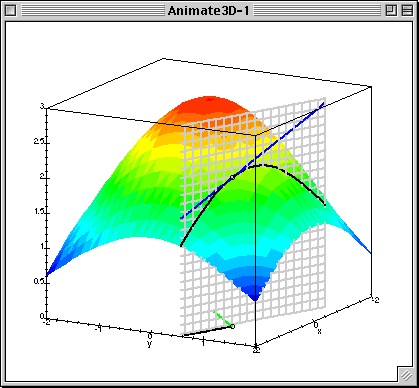
4.1 线性回归模型的代价函数对参数的偏导数

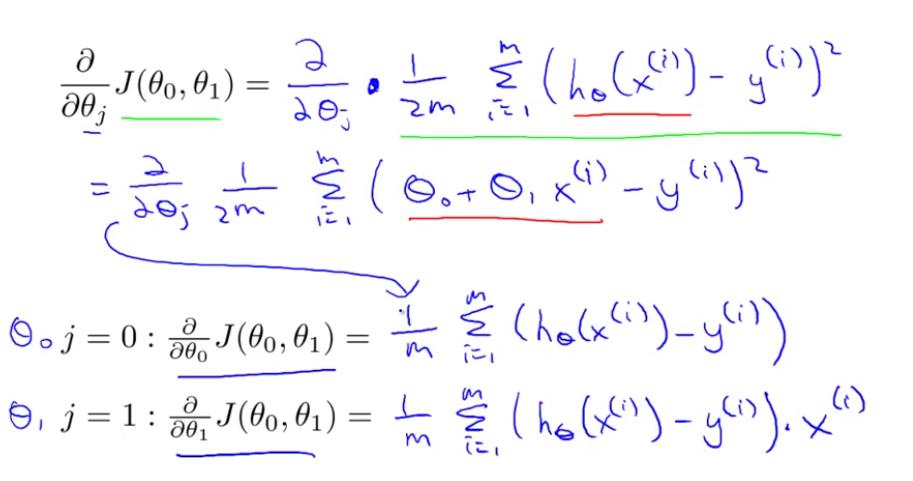
还是以两个参数为例，每个参数都有一个偏导数，且综合了所有样本的信息。

4.2 逻辑回归模型的代价函数对参数的偏导数

根据逻辑回归模型的代价函数以及sigmoid函数

$$h_{\theta}(x)=g(\theta^{T}x)$$

$$g(z)=\frac{1}{1+e^{-z}}$$

得到对每个参数的偏导数为

$$\frac{\partial}{\partial\theta_{j}}J(\theta) =\sum_{i=1}^{m}(h_\theta(x^{i})-y^i)x_j^i$$

详细推导过程可以看这里-逻辑回归代价函数的导数

4.3 神经网络中的代价函数对参数的偏导数

这里的计算过程与前面都不一样，后面再补充。

重大修订：

2017.8.14 修改排版，补充对交叉熵的解释

References

---

https://www.quora.com/How-are-the-cost-functions-for-Neural-Networks-derived/answer/Daniel-Watson-22?srid=uIoGQ

https://www.zhihu.com/question/23468713

https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)

https://hit-scir.gitbooks.io/neural-networks-and-deep-learning-zh_cn/content/chap3/c3s3.html

Coursera, Andrew Ng 公开课第一周，第三周，第五周

http://math.stackexchange.com/questions/477207/derivative-of-cost-function-for-logistic-regression

http://math.stackexchange.com/questions/947604/gradient-tangents-planes-and-steepest-direction