【BZOJ5492】校园旅行(图论 搜索优化)

题目链接

大意

给出\(N\)个点，\(M\)条边的一张图，其中每个点都有一个0或1的颜色。

再给出\(Q\)个询问，每次询问查询两个点之间是否存在一条路径，使得路径上的颜色组成的01字符串是一个回文串。（这条路径上的每条边可以重复经过）

思路

首先有一个暴力的想法，我们设\(Ans[u1][u2]=1\)表示\(u1\)~\(u2\)之间存在一条回文串路径。

我们可以将满足\(Ans[u1][u2]=1\)的\(pair(u1,u2)\)放入一个队列中，暴力往外拓展。

每次枚举与\(u1,u2\)相邻的两个点\(v1,v2\)，若\(col[v1]=col[v2]\)，说明\(v1\)~\(v2\)间也有一条回文路径。

故将\(Ans[v1][v2]\)的值更为1，然后将\(pair(v1,v2)\)放入队列，不断循环，直到不能更新。



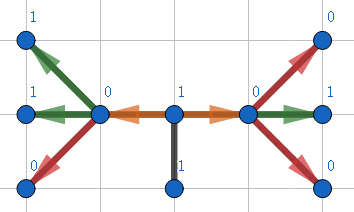
但这样的时间复杂度可以达到\(O(M^2)\)：

假如每个点颜色都一样，那么我们就会枚举到每一个点对，即我们也会枚举到所有的边对。

考虑优化以上算法：

我们将边分为两类，端点颜色相同的边称为第一类，不同称为第二类：

考虑第一类边对答案的影响：

我们将该图仅按第一类边连接起来，那么每个连通块内的颜色都是一样的。

又由于一条边可以经过多次，那么我们只需考虑一个连通块对回文串某段长度奇偶性的影响即可。

• 倘若一个连通块为一个二分图（即不存在奇环），那么这个连通块内任意两点之间的路径长度奇偶性是不变的。
  
  所以我们考虑将该二分图变成一颗树，那么依然满足任意两点间的路径长度奇偶性不变。
• 倘若不是二分图，那么该连通块一定存在某个奇环，那么这个连通块内任意两点之间的路径长度就是可奇可偶的。
  
  对于这种图，我们也可以将它变成一颗树，然后随便在某个点上加个自环就可以了。
  
  因为这样我们还是可以通过走自环点使得路径长度可奇可偶。

---

考虑第二类边对答案的影响：

首先很显然的是，仅用第二类边连成的图一定是一个二分图，那么就又可以套用刚才奇偶性的结论，生成一棵树即可。

这样修改了以后，对答案的正确性是没有影响的，但是边的数量级变为了\(O(N)\)，这样我们就可以直接套用之前的暴力做法，\(O(N^2)\)出解了。

注：文中的“树”在不连通的情况下是指森林。

代码

//#pragma GCC optimize(2)
#include<queue>
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=5005;
const int MAXM=500005;
char c[MAXN];
int Fa[MAXN],Cnt;
int N,M,K,col[MAXN];
int Ans[MAXN][MAXN];
int Col[MAXN],vis[MAXN];
queue<pair<int,int> >Q;
vector<int>P[MAXN],E[MAXN];
struct Edge{int x,y;}s[MAXM];
int Find(int x){return Fa[x]==x?x:Fa[x]=Find(Fa[x]);}
inline void read(int &x){
    x=0;char c=getchar();bool f=0;
    if(c=='-')f=1;
    while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
	if(f==1)x=-x;
}
void Init_BFS(){
	while(!Q.empty()){
		pair<int,int>u=Q.front();Q.pop();
		int u1=u.first,u2=u.second;
		int size1=P[u1].size();
		int size2=P[u2].size();
		for(int i=0;i<size1;i++){
			int v1=P[u1][i];
			for(int j=0;j<size2;j++){
				int v2=P[u2][j];
				if(Ans[v1][v2])continue;
				if(col[v1]!=col[v2])continue;
				Ans[v1][v2]=Ans[v2][v1]=1;
				Q.push(make_pair(v1,v2));
			}
		}
	}
}
int Ok;
int DFS(int u){
	int Ok=0;vis[u]=1;
	int size=E[u].size();
	for(int i=0;i<size;i++){
		int v=E[u][i];
		if(vis[v]){
			if(Col[u]==Col[v])Ok=1;
			continue;
		}
		P[u].push_back(v);
		P[v].push_back(u);
		Q.push(make_pair(u,v));
		Ans[u][v]=Ans[v][u]=1;
		Col[v]=(Col[u]+1)%2;
		if(DFS(v))Ok=1;
	}
	return Ok;
}
int main(){
	scanf("%d%d%d%s",&N,&M,&K,c+1);
	for(int i=1;i<=N;i++)col[i]=c[i]-'0';
	for(int i=1,x,y;i<=M;i++){
		read(x);read(y);
		if(col[x]==col[y]){
			E[x].push_back(y);
			E[y].push_back(x);
		}
		else Cnt++,s[Cnt].x=x,s[Cnt].y=y;
	}
	for(int i=1;i<=N;i++){
		if(vis[i])continue;
		if(DFS(i))P[i].push_back(i);
	}
	for(int i=1;i<=N;i++)
		Ans[i][i]=1,Q.push(make_pair(i,i));
	for(int i=1;i<=N;i++)Fa[i]=i;
	for(int i=1;i<=Cnt;i++){
		int fx=Find(s[i].x);
		int fy=Find(s[i].y);
		if(fx==fy)continue;
		Fa[fx]=fy;
		P[s[i].x].push_back(s[i].y);
		P[s[i].y].push_back(s[i].x);
	}
	Init_BFS();
	for(int i=1,x,y;i<=K;i++){
		scanf("%d%d",&x,&y);
		if(col[x]!=col[y]){
			printf("NO\n");
			continue;
		}
		if(Ans[x][y]==1)puts("YES");
		else puts("NO");
	}
}