(DDS)正弦波形发生器——幅值、频率、相位可调（一）

(DDS)正弦波形发生器——幅值、频率、相位可调

一、项目任务：

• 设计一个幅值、频率、相位均可调的正弦波发生器。
  • 频率每次增加1kHz。
  • 相位每次增加 2*PI/256
  • 幅值每次增加两倍

二、文章内容：

1. DDS的核心原理。
2. 分别使用两种方式完成频率可调（a、b），并且进行对比（c），最后对b进行优化（d）。
3. 完成赋值、频率、相位可调的正弦波形发生器。（文章二）

1、DDS核心原理：

• 读取ROM中存储的波形数据获得一个基础波形（基频），之后不断进行循环读取。

• 幅值——ROM中取得数据使用乘法进行放大。

• 相位——改变从ROM中读取时，地址的初值。

• 调频——ROM时钟固定，控制读取ROM的地址来控制输出频率：

  • 系统时钟为50MHz，ROM位宽为8，深度256。
  • 有一个思路就是：先确定一个最小的频率，然后不断的对该频率进行放大，即可以控制频率的大小。反过来讲，就是先使用一种最慢的控制地址的读取ROM数据的方式，然后缩小读取的时间即可放大频率。
  • 那么如何确定基频的大小呢？根据采取方法不同基频大小不定，但是为了频率的准确有以下几点需要注意：
    • 基频小些比较好
    • 基频越接近1、0.1、0.01、0.001······越好

2、两种产生基频的方式

a、32位寄存器基频：

• 使用一个32为寄存器，将高8位作为ROM的地址位，其余24位无特殊作用，寄存器按照系统时钟进行自加，此时高8位的变化频率与用于自加的系统时钟频率有了成倍的关系，很像计数器计数频率变化但存在区别，之后会讨论到。

• 系统时钟为50MHz，ROM位宽为8，深度256。那么基础频率为：

  \[% MathType!MTEF!2!1!+-
  % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
  % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
  % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
  % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs
  % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai
  % aabeqaamaabaabauaajqgaG9FaceaapgGaamOzaOWaaSbaaSqaaiaa
  % dkgaaeqaaOGaeyypa0ZaaSaaaeaacaaI1aGaaGimaiabgEna0kaaig
  % dacaaIWaWaaWbaaSqabeaacaaI2aaaaaGcbaGaaGOmamaaCaaaleqa
  % baGaaGOmaiaaisdaaaGccqGHxdaTcaaIYaGaaGynaiaaiAdaaaGaey
  % ypa0JaaGimaiaac6cacaaIWaGaaGymaiaaigdacaaI2aGaaGinaiaa
  % igdacaaI1aGaamisaiaadQhaaaa!5ABC!
  {f_b} = \frac{{50 \times {{10}^6}}}{{{2^{24}} \times 256}} = 0.0116415Hz
  \]

• 所以产生一个1kHz的正弦波（1kHz的ROM地址变化速度）只需要将基频放大1000/0.0116415 = 85899.34592，即扩大85899倍。

• 所以若想频率每次增加1kHz，在低24位每次自加85899即可，此时85899为频率控制字。

• module addr_ctrl(
      input  clk,
      input  rst_n,
  
      output  [7:0] addr
  );
  
  reg [31:0] address;
  assign addr = address[31:24];
  
  always @(posedge clk,negedge rst_n)
  begin
      if(rst_n == 0)
          address <= 32'd0;
      else
          //address <= address + 32'd858996;    //10kHz
          address <= address + 32'd85899;
  end 
  
  endmodule
  

• 

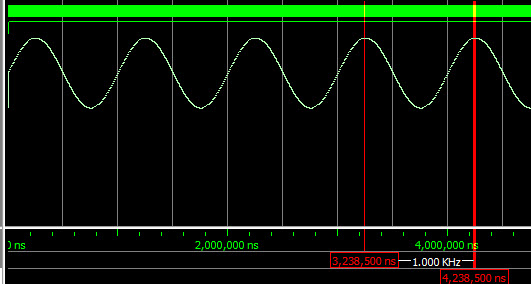
• 通过仿真可以看到准确的产生了1kHz的正弦波

• //顶层
  module digital_adds(
      input  clk,
      input  rst_n,
  
      output [7:0] data
  );
  
  wire [7:0] addr;
  
   addr_ctrl addr_ctrl_inst(
      .clk  (clk),
      .rst_n(rst_n),
  
      .addr (addr)
  );
  
  rom1	rom1_inst (
  	.address ( addr ),
  	.clock ( clk ),
  	.q ( data )
  	);
  
  endmodule
  

• //测试文件
  `timescale 1ns/1ps
  module digital_adds_tb();
      reg  clk;
      reg  rst_n;
  
      wire [7:0] data;
  
   digital_adds digital_adds_inst(
      .clk  (clk),
      .rst_n(rst_n),
  
      .data (data)
  );
  
  initial clk = 1;
  always #10 clk = !clk;
  
  initial begin                         //同步复位信号需要时钟上升沿检测
      rst_n = 0;
      #200
      rst_n = 1;
      #5000000
  
      $stop;
  end
  
  endmodule
  

---

b、计数器产生基频计算：

• 系统时钟为50MHz，ROM位宽为8，深度1024。

• 使用计数器产生1Hz的基频，方便之后扩频计算

  \[% MathType!MTEF!2!1!+-
  % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
  % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
  % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
  % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs
  % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai
  % aabeqaamaabaabauaajqgaG9FaceaapgGaamOzaOWaaSbaaSqaaiaa
  % dkgaaeqaaOGaeyypa0ZaaSaaaeaacaaIXaGaaGimamaaCaaaleqaba
  % GaaGyoaaaaaOqaaiaaikdacaaIWaGaey41aqRaaGymaiaaicdacaaI
  % YaGaaGinaiabgEna0kaaisdacaaI4aGaaGioaiaaisdacaaI4aaaai
  % abg2da9iaaigdacaGGUaGaaGimaiaaicdacaaIWaGaaGimaiaaicda
  % caaIYaGaaGynaiaaiAdacaaIWaGaaGimaiaaicdacaaI2aGaaGynai
  % aadIeacaWG6baaaa!6128!
  {f_b} = \frac{{{{10}^9}}}{{20 \times 1024 \times 48828}} = 1.0000025600065Hz
  \]

• 使用1024个数据，每个为20ns，共计48848次。

• 则频率控制字为1000时即可产生1kHz的正弦波。

• //频率控制模块
  module addr_ctrl(
      input  clk,
      input  rst_n,
  
      output reg [9:0] addr
  );
  
  reg [15:0] cnt;
  
  always @(posedge clk,negedge rst_n)
  begin
      if(rst_n == 0)
          cnt <= 16'd0;
      else
          if(16'd48848 <= cnt)
              cnt <= 16'd0;
          else
              cnt <= cnt + 16'd1000;  //频率控制字1kHz的基频
  end 
  
  always @(posedge clk,negedge rst_n)
  begin
      if(rst_n == 0)
          addr <= 10'd0;
      else
          if(16'd48848 <= cnt)
              addr <= addr + 10'd1;
          else
              addr <= addr;
  end 
  
  endmodule
  

• 

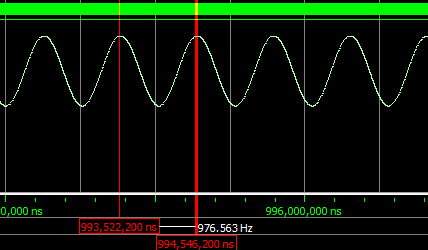
• 图中可以看到，得到了977Hz的正弦波，存在着较大的误差，实际效果与理论计算严重不符，这是为什么呢？

---

c、对比

• 32位寄存器使用低位向高位进位可以确保每次加的数据都产生了效果，都向高位产生了进位。

• 相比使用计数器产生的基频很准确但是有着非常致命的缺点：

  • 当频率控制字不能被计数器最大值整除，即当频率控制字即将累加到计数器最大值时，由于不能整除。可能还差一点点计数器就符合判断要求了，即已经非常接近我们预设的地址变化频率了，但是仍然不满足判断标准，必须等到下一次频率控制字的累加才可以使地址加一，这里就产生了理论计算和实际情况不同的问题。

  • 其关键就是计数器进位是严格按照条件执行的少一点会不执行而多一点会被吞掉直接置零，舍弃掉了余数，并且由于cnt的初值从零开始且每次增加1000，说以实际上计算为：

    \[% MathType!MTEF!2!1!+-
    % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
    % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
    % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
    % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs
    % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai
    % aabeqaamaabaabauaajqgaG9FaceaapgGaamOzaOWaaSbaaSqaaiaa
    % dkgaaeqaaOGaeyypa0ZaaSaaaeaacaaIXaGaaGimamaaCaaaleqaba
    % GaaGyoaaaaaOqaaiaaikdacaaIWaGaey41aqRaaGymaiaaicdacaaI
    % YaGaaGinaiabgEna0kaacIcacaaI0aGaaGyoaiabgUcaRiaaigdaca
    % GGPaGaey41aqRaaGymaiaaicdacaaIWaGaaGimaaaacqGH9aqpcaaI
    % WaGaaiOlaiaaiMdacaaI3aGaaGOnaiaaiwdacaaI2aGaaGOmaiaaiw
    % dacaWGibGaamOEaaaa!6290!
    {f} = \frac{{{{10}^{12}}}}{{20 \times 1024 \times (49 + 1) \times 1000}} = 976.5625Hz
    \]

• 该计算结果和仿真得到的结果相同，并且可以看到仿真保留了三位有效数字。

• 也就是说b法误差有两点原因：

  • 忘记对cnt从零开始进行处理。
    • 算法本身带来的一定误差。

• 而低位向高位进位得到的计数器：

  • 从零开始几乎不影响最终效果因为不参与循环不会累计误差
  • 不会舍弃余数而是累加了起来

• 传统方法b还是好用一些，，，

• 我竟然品出了一点连续和离散的感觉出来。

---

d、对b进行修改

• 理论计算：

  \[% MathType!MTEF!2!1!+-
  % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
  % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
  % 4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
  % pepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs
  % 0-yqaqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaai
  % aabeqaamaabaabauaajqgaG9FaceaapgGaamOzaOWaaSbaaSqaaiaa
  % dkgaaeqaaOGaeyypa0ZaaSaaaeaacaaIXaGaaGimamaaCaaaleqaba
  % GaaGymaiaaikdaaaaakeaacaaIYaGaaGimaiabgEna0kaaigdacaaI
  % WaGaaGOmaiaaisdacqGHxdaTcaaI0aGaaGyoaiabgEna0kaaigdaca
  % aIWaGaaGimaiaaicdaaaGaeyypa0JaaGyoaiaaiMdacaaI2aGaaiOl
  % aiaaisdacaaI5aGaaGOmaiaaiodacaaI0aGaaGOnaiaaiMdacaWGib
  % GaamOEaaaa!61D7!
  {f_b} = \frac{{{{10}^{12}}}}{{20 \times 1024 \times 49 \times 1000}} = 996.4923469Hz
  \]

• 

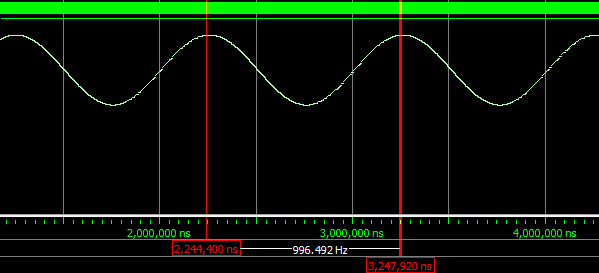
• 可以看到经过改进后：

  • 理论计算和仿真验真结果相符。
  • 产生波形的频率精度尚可。

• module addr_ctrl(
      input  clk,
      input  rst_n,
  
      output reg [9:0] addr
  );
  
  reg [15:0] cnt;
  
  always @(posedge clk,negedge rst_n)
  begin
      if(rst_n == 0)
          cnt <= 16'd0;
      else
          if(16'd48 <= cnt)  //只要取倍数就可以了，并且要注意cnt初值为零已经多循环了一次
              cnt <= 16'd0;
          else
              cnt <= cnt + 16'd1;   //频率控制字1kHz的基频
  end 
  
  always @(posedge clk,negedge rst_n)
  begin
      if(rst_n == 0)
          addr <= 10'd0;
      else
          if(16'd48 <= cnt)
              addr <= addr + 10'd1;
          else
              addr <= addr;
  end 
  
  endmodule
  

---

至此文章1、2部分已经完成，第三部分的整体代码见下文

---

备注：

• ROM可以通过时钟和地址两种控制方式来使用。
• 第一个方法的图中我们可以看到准确的产生1kHz的正弦波，但是基频并非整数，为什么能够准确的产生1kHz的正弦波呢？是在哪一步忽略的，由于没有AD/DA也没有示波器没办法探究真实情况。

---

作者：野客居/13tree

出处：https://www.cnblogs.com/13tree/

本文版权归作者所有，如需转载请保留此段声明。