几何 三垂模型 及 正方形 及 弦图 及 jio拉jio模型 及 中位线

Q:$AO\bot OB,AO=OB,CO\bot OD,CO=OD,BC\bot EF$ 求证 $E$ 为 $AD$ 中点

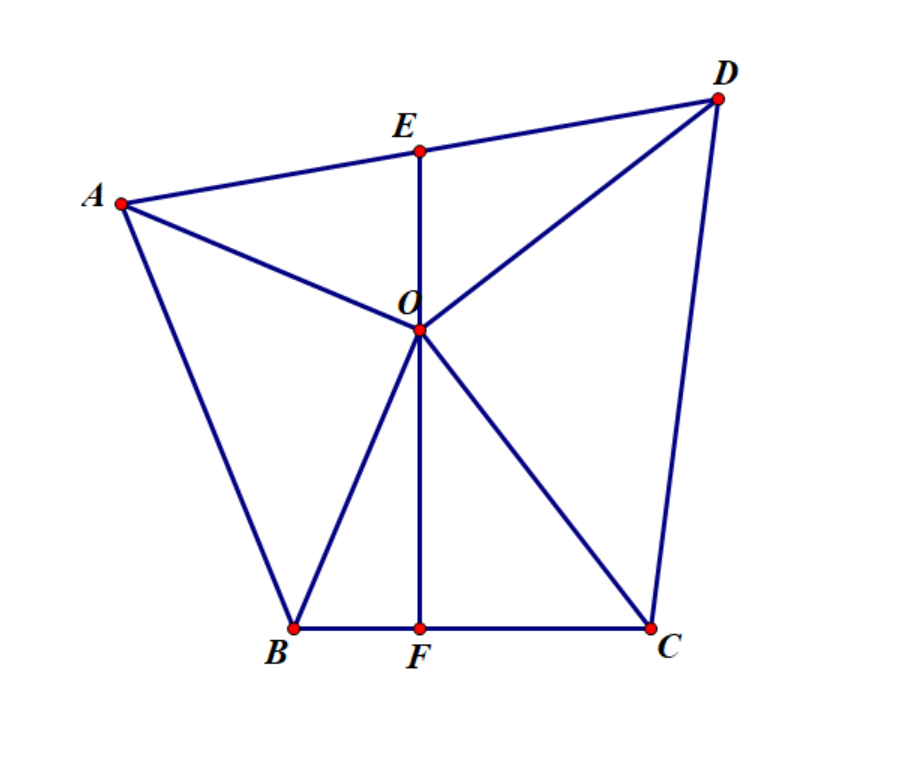
A:作如图 $AI\bot IH\bot HD$

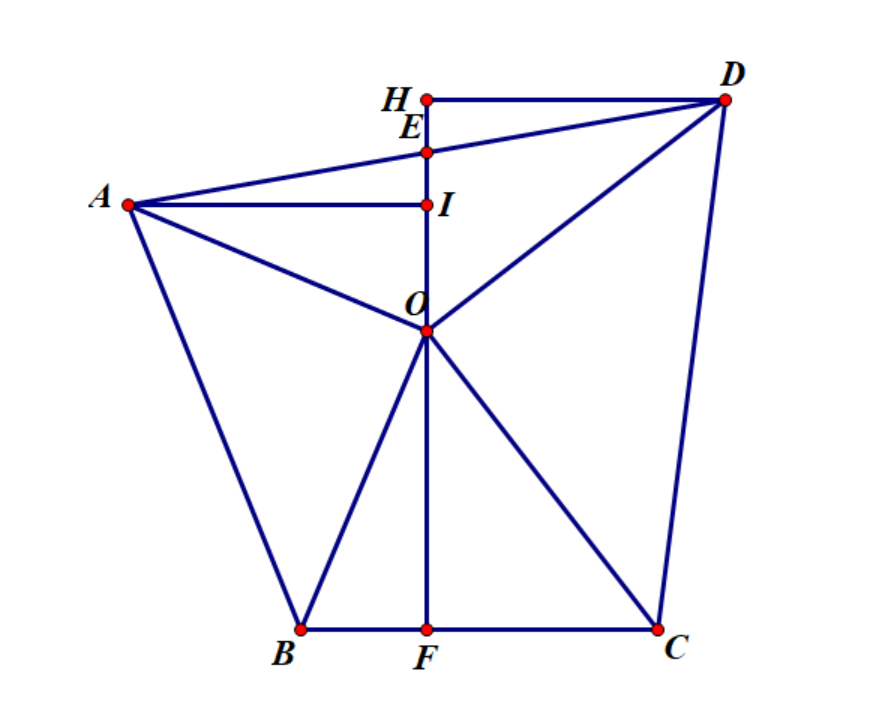
$\because AO=OB,\angle AIO=\angle OFB,\angle IAO=\angle BOF$

$\therefore \triangle AIO\cong \triangle BOF$

$\therefore AI=OF$

同理可得 $HD=OF=AI$

$\therefore \triangle AIE\cong \triangle EHD$

$\therefore AE=ED$ 即 $E$ 为 $AD$ 中点

此题图中左右两侧均为三垂模型，可构造全等三角形

接下来一道包含内三垂和外三垂的题目:

Q:$AB\bot AC,AB=AC,AD\bot AE,AD=AE,AF\bot FC$ 求证 $G$ 为 $BE$ 中点

A:作如图 $BH\bot HI\bot IE$

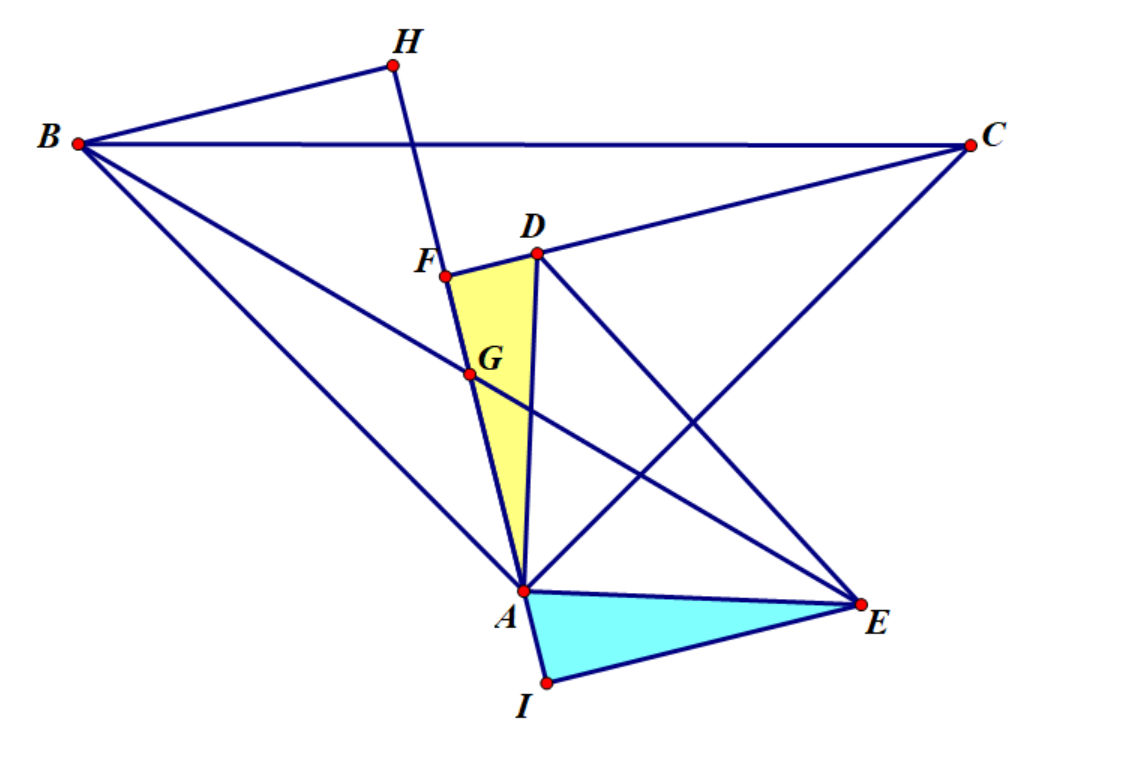
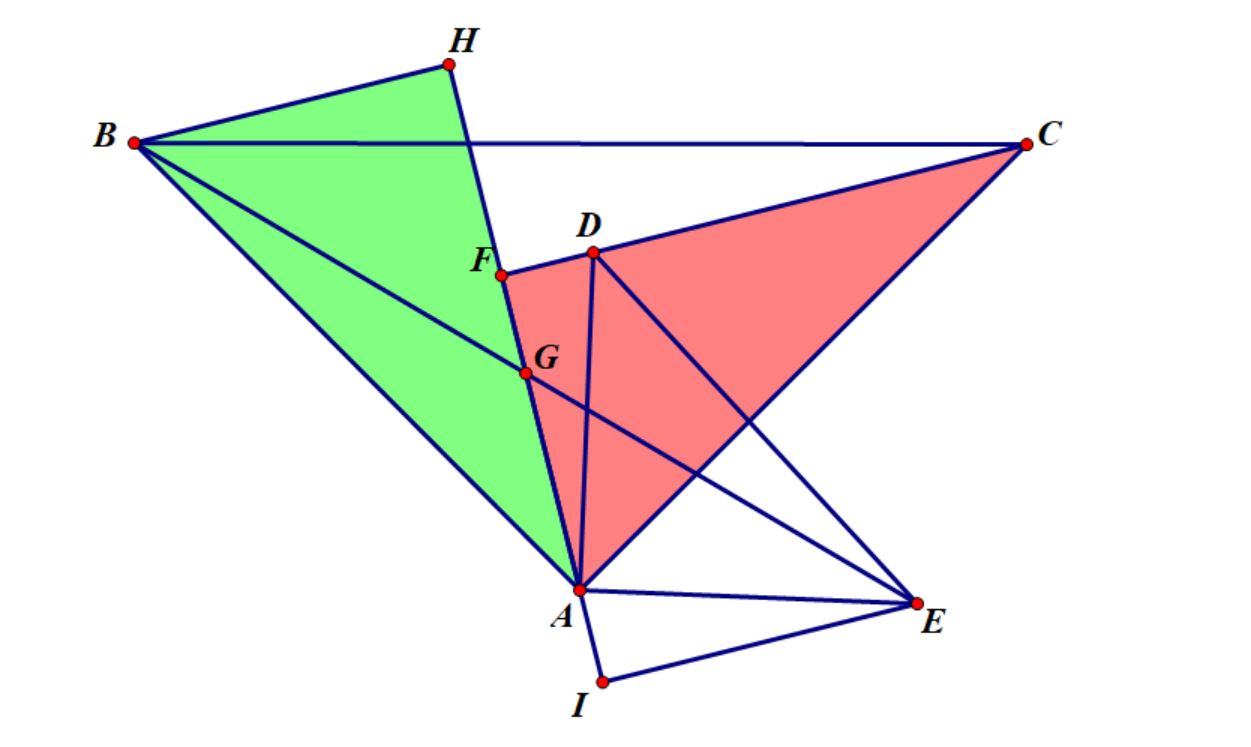
(为美观，过程已被删减)

$\because \triangle YELLOW\cong \triangle BLUE,\triangle GREEN\cong \triangle RED$

$\therefore IE=AF=BH$

$\therefore \triangle BHG\cong \triangle GIE$

$\therefore BG=GE$ 即 $G$ 为 $BE$ 中点

Q: $\Box ABCD$ 中取一点 $E$ 使 $AE\bot EB,AE=1,CE=5 $ 求DE的长

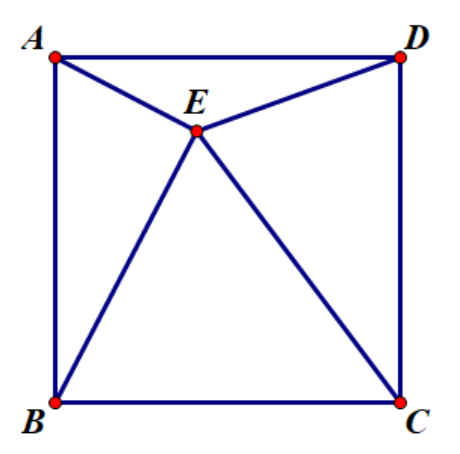
A:作如图

显然 $\triangle ABE\cong \triangle BCF\cong \triangle CDG\cong \triangle DAH$

则 $AE=BF=CG=DH=1$

设 $EF=FG=GH=HE=x$

根据勾股定理

$EF^2+FC^2=EC^2$

$x^2+(1+x)^2=25$

$x_1=3,x_2=-4$ ( $x_2$ 舍)

$EH^2+HD^2=DE^2$
 $x^2+1=DE^2$
 $DE^2=10$
 $DE=\sqrt{10}$

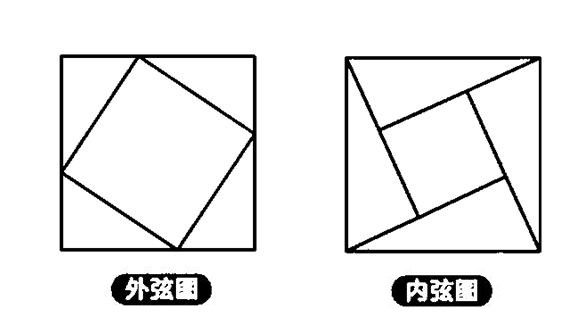
此类图称为正方形的内弦图

正方形的弦图为多个三垂模型叠加而来

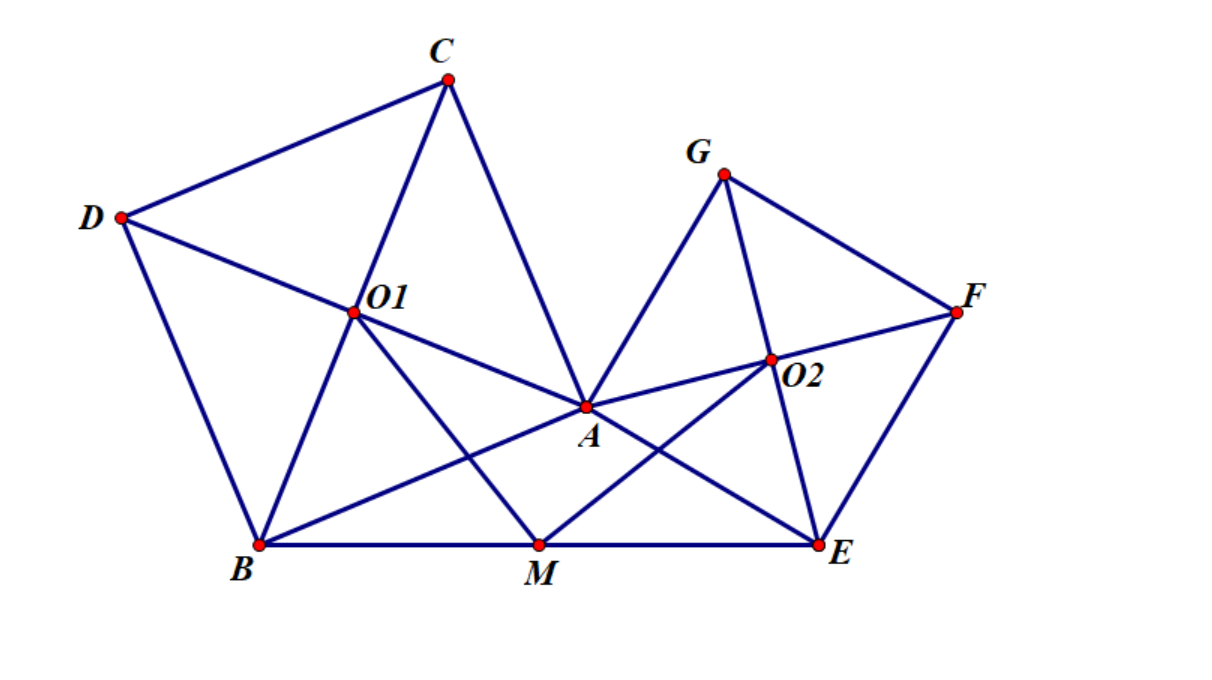
Q:如图,$O_1,O_2$分别为两个正方形的中心点,$M$是$BE$的中点,求证$MO_1=MO_2,MO_1\perp MO_2$

A1:（jio拉jio模型：手拉手变式）如图,倍长$O_2M$至$H$

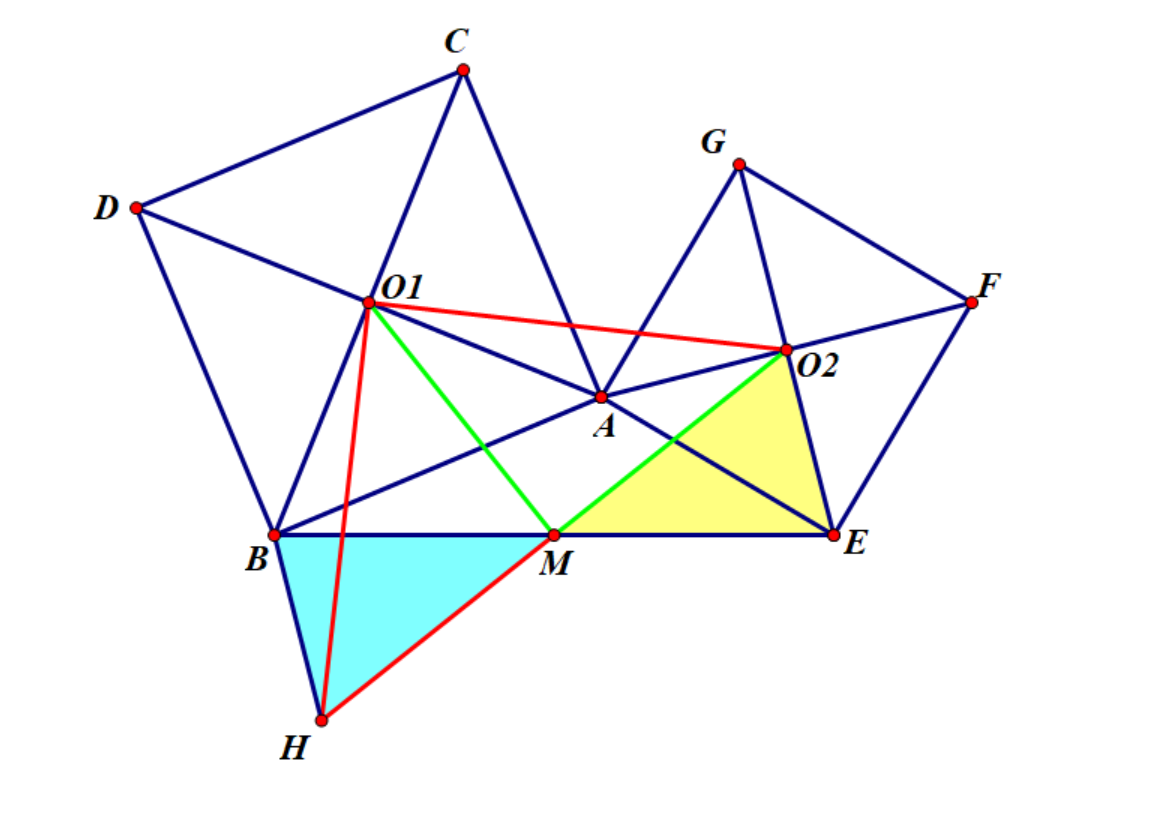
显然$\triangle O_2EM\cong \triangle BHM$

$AO_2=O_2E=BH,AO_1=O_1B$

(导角过程略)$\angle HBO_1=\angle O_1AO_2$

$\triangle HBO_1\cong \triangle O_1AO_2$

$\angle HO_1O_2=\angle BO_1A=90^{\circ},HO_1=HO_2$(等腰直角三角形)

$MO_1=MO_2,MO_1\perp MO_2$

A2:（三角形中位线）连接 $CE,BG$ 则 $CE=2MO_1,GB=2MO_2$

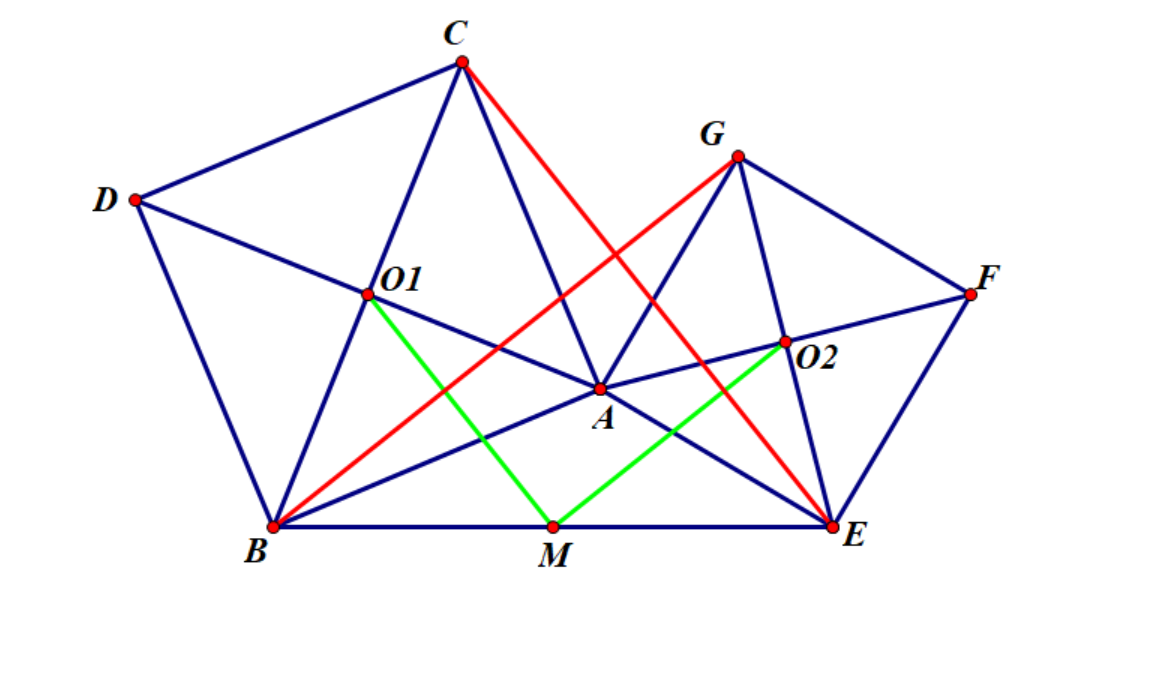
$\because \triangle BAG\cong \triangle CAE$(证明略)

$\therefore CE=BG,CE\perp BG$(证明略)

$\therefore MO_1=MO_2,MO_1\perp MO_2$