机器学习之支持向量机（python）

参考链接：https://blog.csdn.net/weixin_33514582/article/details/113321749、https://blog.csdn.net/weixin_44196785/article/details/109263326。

一、简介

　　支持向量机 (Support Vector Machine) 是由Vapnik等人于1995年提出来的，之后随着统计理论的发展，支持向量机 SVM 也逐渐受到了各领域研究者的关注，在很短的时间就得到了很广泛的应用。支持向量机是被公认的比较优秀的分类模型。同时，在支持向量机的发展过程中，其理论方面的研究得到了同步的发展，为支持向量机的研究提供了强有力的理论支撑。

1 SVM、SVC、SVR三者的区别

• SVM=Support Vector Machine 是支持向量机
• SVC=Support Vector Classification就是支持向量机用于分类，
• SVR=Support Vector Regression.就是支持向量机用于回归分析

2 算法（python-sklearn）

SVM模型的几种

• svm.LinearSVC Linear Support Vector Classification.
• svm.LinearSVR Linear Support Vector Regression.
• svm.NuSVC Nu-Support Vector Classification.
• svm.NuSVR Nu Support Vector Regression.
• svm.OneClassSVM Unsupervised Outlier Detection.
• svm.SVC C-Support Vector Classification.
• svm.SVR Epsilon-Support Vector Regression.

二、svr预测

1 SVR原理简述

线性回归的基本模型为：

 ，从某方面说这和超平面的的表达式：

 有很大的相似性。但SVR认为只要 与

 不要偏离太大即算预测正确，

 为拟合精度控制参数。如图所示：

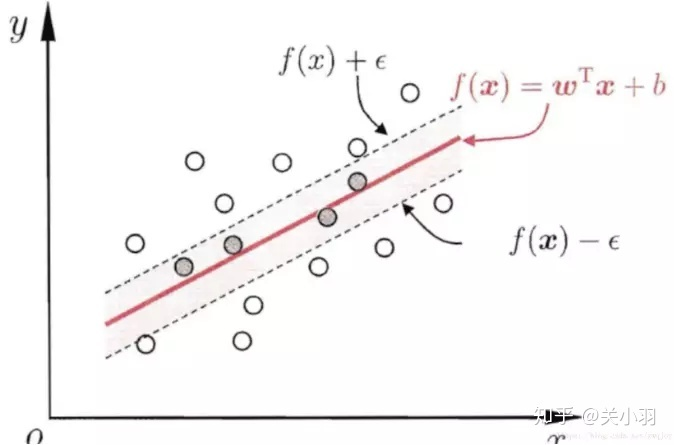
　　　　　　　　　　SVR 示意图

　　从图例中分析，支持向量机回归与线性回归相比，支持向量回归表示只要在虚线内部的值都可认为是预测正确，只要计算虚线外部的值的损失即可。考虑到SVM中线性不可分的情形，在引入松弛变量

 最终得出支持向量机回归的最优化问题：

 ;

 ;

 ;

 。

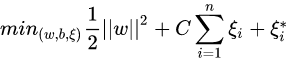
引入拉格朗日乘数，经过一系列求解与对偶，求的线性拟合函数为：

 ;

 为拉格朗日朗日乘子。

引入核函数，则得：

2 python函数介绍

sklearn.svm.SVR（
    kernel ='rbf'，
    degree = 3，
    gamma ='auto_deprecated'，
    coef0 = 0.0，
    tol = 0.001，
    C = 1.0，
    epsilon = 0.1，
    shrinking = True，
    cache_size = 200，
    verbose = False，
    max_iter = -1
 ）
'''
kernel:指定要在算法中使用的内核类型。它必须是'linear'，'poly'，'rbf'， 'sigmoid'，
'precomputed'或者callable之一。

degree： int，可选（默认= 3）多项式核函数的次数（'poly'）。被所有其他内核忽略。

gamma ： float，（默认='auto'）,'rbf'，'poly'和'sigmoid'的核系数。当前默认值为'auto'，
它使用1 / n_features。

coef0 ： float，（默认值= 0.0）核函数中的独立项。它只在'poly'和'sigmoid'中很重要。

tol ： float，（默认值= 1e-3）容忍停止标准。

C ： float，可选（默认= 1.0）错误术语的惩罚参数C.

epsilon ： float，optional（默认值= 0.1）epsilon在epsilon-SVR模型中。
它指定了epsilon-tube，其中训练损失函数中没有惩罚与在实际值的距离epsilon内预测的点。

shrinking ： 布尔值，可选（默认= True）是否使用收缩启发式。

cache_size ： float，可选，指定内核缓存的大小（以MB为单位）。

verbose ： bool，默认值：False 启用详细输出。请注意，
此设置利用libsvm中的每进程运行时设置，如果启用，则可能无法在多线程上下文中正常运行。

max_iter ： int，optional（默认值= -1） 求解器内迭代的硬限制，或无限制的-1
'''

3 示例代码

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
from sklearn.metrics import r2_score

np.random.seed(0)

x = np.random.randn(80, 2)
y = x[:, 0] + 2*x[:, 1] + np.random.randn(80)

clf = SVR(kernel='linear', C=1.25)
x_tran,x_test,y_train,y_test = train_test_split(x, y, test_size=0.25)
clf.fit(x_tran, y_train)
y_hat = clf.predict(x_test)

print("得分:", r2_score(y_test, y_hat))

r = len(x_test) + 1
print(y_test)
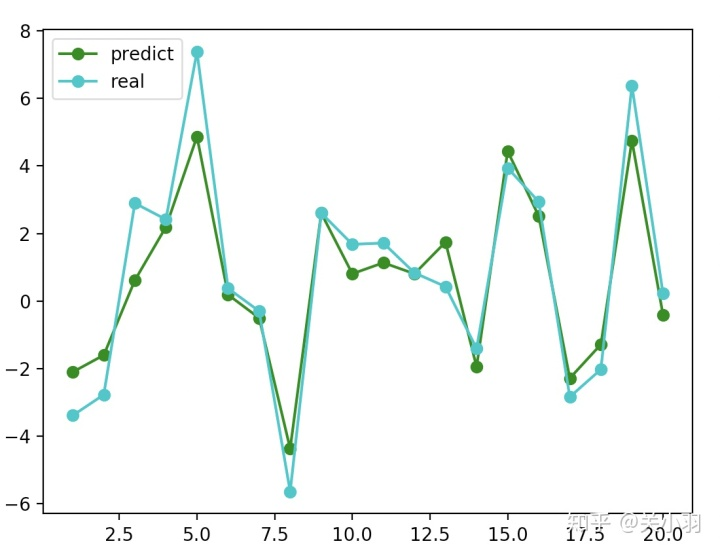
plt.plot(np.arange(1,r), y_hat, 'go-', label="predict")
plt.plot(np.arange(1,r), y_test, 'co-', label="real")
plt.legend()
plt.show()

三、svm代码

1 线性支持向量机

#encoding=utf8
from sklearn.svm import LinearSVC

def linearsvc_predict(train_data,train_label,test_data):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********#
    clf = LinearSVC(dual=False)
    clf.fit(train_data,train_label)
    predict = clf.predict(test_data)
    #********* End *********#
    return predict

2 非线性支持向量机

#encoding=utf8
from sklearn.svm import SVC

def svc_predict(train_data,train_label,test_data,kernel):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
          kernel(str):使用核函数类型:
              'linear':线性核函数
              'poly':多项式核函数
              'rbf':径像核函数/高斯核
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********#
    clf =SVC(kernel=kernel)
    clf.fit(train_data,train_label)
    predict = clf.predict(test_data)
    #********* End *********#
    return predict

3 序列最小优化算法

#encoding=utf8
import numpy as np
class smo:
    def __init__(self, max_iter=100, kernel='linear'):
        '''
        input:max_iter(int):最大训练轮数
              kernel(str):核函数，等于'linear'表示线性，等于'poly'表示多项式
        '''
        self.max_iter = max_iter
        self._kernel = kernel
    #初始化模型
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 错误惩罚参数
        self.C = 1.0
    #********* Begin *********#
    #kkt条件
    def _KKT(self, i):
        y_g = self._g(i)*self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1
    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j]*self.Y[j]*self.kernel(self.X[i], self.X[j])
        return r
    # 核函数,多项式添加二次项即可
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k]*x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2
        return 0
    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]
    #初始alpha
    def _init_alpha(self):
        # 外层循环首先遍历所有满足0<a<C的样本点，检验是否满足KKT
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
        for i in index_list:
            if self._KKT(i):
                continue
            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j
    #选择alpha参数
    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha
    #训练
    def fit(self, features, labels):
        '''
        input:features(ndarray):特征
              label(ndarray):标签
        '''
        self.init_args(features, labels)
        for t in range(self.max_iter):
            i1, i2 = self._init_alpha()
            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
                H = min(self.C, self.alpha[i1]+self.alpha[i2])
            else:
                L = max(0, self.alpha[i2]-self.alpha[i1])
                H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2*self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                continue
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E2 - E1) / eta
            alpha2_new = self._compare(alpha2_new_unc, L, H)
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2
            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
    def predict(self, data):
        '''
        input:data(ndarray):单个样本
        output:预测为正样本返回+1，负样本返回-1
        '''
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
        return 1 if r > 0 else -1
    #********* End *********# 

4 支持向量回归

#encoding=utf8
from sklearn.svm import SVR

def svr_predict(train_data,train_label,test_data):
    '''
    input:train_data(ndarray):训练数据
          train_label(ndarray):训练标签
    output:predict(ndarray):测试集预测标签
    '''
    #********* Begin *********#
    svr = SVR(kernel='rbf',C=100,gamma= 0.001,epsilon=0.1)
    svr.fit(train_data,train_label)
    predict = svr.predict(test_data)

    #********* End *********#
    return predict