字典树（Trie）

终于学会字典树了，真开心（然后就滚过来写总结了）。

首先，字典树到底是个什么东西呢？请看下面这段话：

字典树，常被用来保存与查找大量的字符串，它利用了字符串之间的公共前缀来节约时间，但它的空间花费较大。 ——整理自百度百科

举个例子，现在有六个字符串，分别是：“he”、“her”、“sheep”、“she”、“shem”、“me”，用这几个字符串构造的trie就长下面这样：

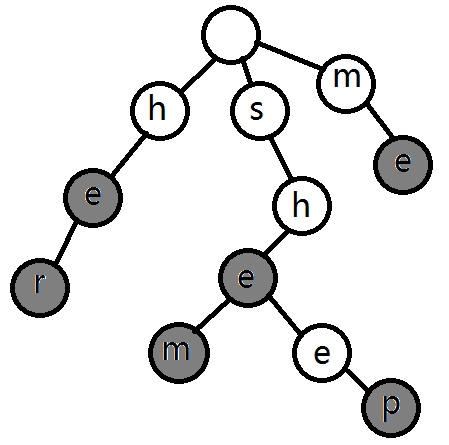
我们可以发现，在trie中，除了根节点，其它的每个节点都代表着一个字符。如果节点是灰色的，就表示此节点是一个字符串结束的位置。

我们先来看一看trie是如何运作的吧。

比如说，我现在要“her”这一个字符串是否存在，我们就只需要顺着树边往下找，像下面这样子：

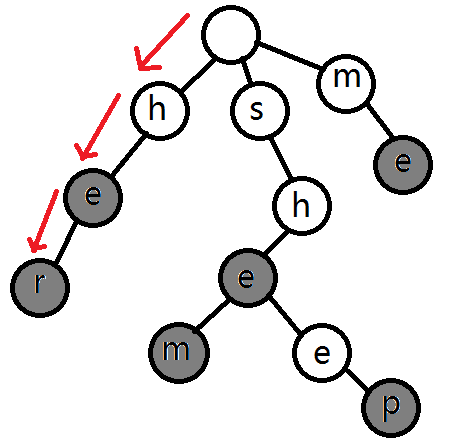
如果可以一直顺着树边找到结束，并且结束点是一个灰色节点，那么就说明“her”这一个字符串是存在的。

再举个例子，假如现在要判断的是“hen”这一个字符串是否存在（显然它是不存在的），我们也是像刚才那样子顺着树边往下找：

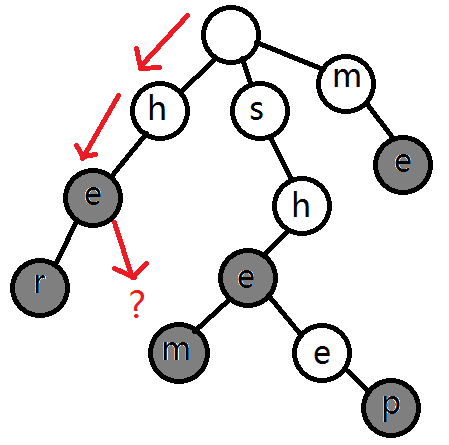
可以发现，这一次我们在走到“e”这一个节点后就没有看到储存的字符为“n”的节点了，这就说明“hen”这一个字符串是不存在的。

说到这里，大家对trie的基本功能应该已经有了一个比较清晰的认识了。有人可能会说，判断一个字符串在一个字符串集合中是否存在，直接用哈希不就搞定了吗？是的，确实是这样。不过trie更容易扩展。比如说，AC自动机就是在trie上使用了kmp算法的思想实现的。所以，学习trie还是很有必要的。

好，说了这么多理论，我们接下来就来说一下trie树的实现思路吧。

首先肯定是讲如何在一棵trie中插入字符串了。在trie中插入字符串的思路很简单，我们来举个例子（举例子大法好啊），比如说现在我们要在一棵空trie中插入一个字符串“”sheep”。首先，一棵空trie是下面这样子的：

（只有一个根节点，而且这个根节点不储存任何字符信息）

然后，我们来弄一个箭头指向这个根节点，表示我们现在的位置就是在这个根节点：

接下来，我们来插入“sheep”中的第一个字符“s”，因为当前箭头指向的节点并没有“s”这个儿子，所以我们来新建一个，并将箭头指向这一个“s”：

紧接着，像上面那样依次插入“sheep”的后几个字符：“h”、“e”、“e”、“p”：

将“sheep”中的所有字符全部插入完毕后，我们再将当前箭头指向的节点标记为灰色，表示这一个结点是“sheep”这一个字符串的结束位置，这个应该很容易理解吧？如下图所示：

这样我们就将“sheep”插入到这一棵trie中了，但是如果我们还要插入一个字符串“shem”的话，又该怎么处理呢？我们再来模拟一下。

首先，箭头肯定是指向根节点：

然后，我们看一下“shem”的第一个字符“s”。唉？当前节点已经有儿子“s”了，那我们就直接指向那里：

接着，我们看一下“shem”的第二个字符“h”，唉？当前节点已经有儿子“h”了，那我们还是直接指向那里：

接下来，我们看一下“shem”的第三个字符“e”，唉？当前节点已经有儿子“e”了，那我们还是直接指向那里：

紧接着，我们看一下“shem”的第四个字符“m”，唉？当前节点没有儿子“m”，那我们就新建一个儿子节点“m” ，然后指向那里：

最后标记成灰色就好啦！

综上所述，trie的插入思路可以总结为一点：如果有就直接上，没有就新建。（是不是很精辟）

trie的插入代码如下：

    int tot=0,tri[size][26];
    bool end[size];
void cr(char* st)
{
    int len=strlen(st),p=1;//p就是那个“箭头”
    for(int i=0;i<len;i++)//依次插入这个字符串的每一个字符
    {
        int t=st[i]-97;
        if(tri[p][t]==0) tri[p][t]=++tot;//如果没有符合要求的节点就新建
        p=tri[p][t];//“箭头”指向下一个节点
    }
    end[p]=true;//标记当前节点为灰色（就是标记当前节点是一个字符串的结束位置）
}

上面的代码中的size为给出的所有字符串中字符数量的总和，因为最糟糕的情况就是将每个字符都建了一个节点，所以trie的节点最多也不会超过所有字符串中字符数量的总和。

把tri数组的第二维定为26是因为trie处理的字符串一般都是只由26个小写英文字母组成的（当然，trie也能处理其它字符串，这里只是“一般”而已），这要视情况而定。

那么trie的查找操作呢？这个前面其实已经讲过了，这和插入的思路是大同小异的，那就直接丢代码吧：

bool cz(char* st)
{
    int len=strlen(st),p=1;//p就是那个“箭头”
    for(int i=0;i<len;i++)//依次查找这个字符串的每一个字符
    {
        int t=st[i]-97;
        if(tri[p][t]==0) return false;//如果没有符合要求的节点就说明找不到了
        p=tri[p][t];//“箭头”指向下一个节点
    }
    if(end[p]) return true;//如果当前节点是某个字符串的结束位置就说明找到了
    return false;//否则就说明找不到了
}

如果明白了插入操作是肯定可以看得懂上面的代码的，基本上是如法炮制。

从上述代码不难看出trie插入与删除的时间复杂度都是O(L)的，其中L为插入或查找的字符串的长度，trie的时间复杂度还是挺优秀的嘛。

trie裸题： Luogu P2580 于是他错误的点名开始了

好了，终于写完了。。。

由于博主是个蒟蒻，所以肯定会有一些地方写得不清楚，还请大家批评指正。

0=w=0