【Java 8】Stream中flatMap方法

在java 8 Stream中，flatMap方法是一个维度升降的方法

举例说明

给 定 单 词 列 表[“Hello”,“World”] ，要返回列表 [“H”,“e”,“l”, “o”,“W”,“r”,“d”] 。

使用map方法，代码如下：

public class StreamStr {
	public static void main(String[] args) {
		List<String> list = Arrays.asList("tom", "jame", "jerry", "hello");
		Stream<String> stream = list.stream();
		Stream<String[]> streamString = stream.map(s->s.split(""));
		Stream<Stream<String>> map = streamString.map(Arrays::stream);

		// List<Stream<String>> collect = map.collect(Collectors.toList());
		// System.out.println(collect);

		map.forEach(x->{
			x.forEach(s->{
				System.out.println(s);
			});
		});

	}
}

t
o
m
j
a
m
e
j
e
r
r
y
h
e
l
l
o

转变类型为：String -> String[]-> Stream<String>，当前维度从一维变成二维，map本身不能降为，执行如下

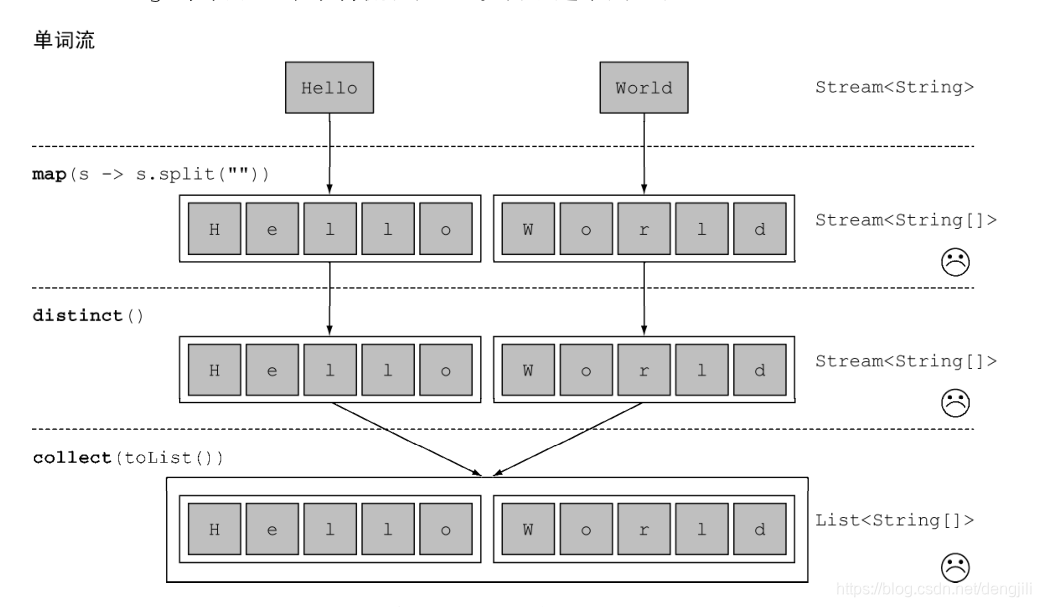
引入flatMap方法

具体代码变化如下：

public class StreamStr {
	public static void main(String[] args) {
		List<String> list = Arrays.asList("tom", "jame", "jerry", "hello");
		Stream<String> stream = list.stream();
		Stream<String[]> streamString = stream.map(s->s.split(""));
		Stream<String> map = streamString.flatMap(Arrays::stream);

		map.forEach(x->{
			System.out.println(x);
		});

	}
}

t
o
m
j
a
m
e
j
e
r
r
y
h
e
l
l
o

这里是从二维降为一维，逻辑如下：

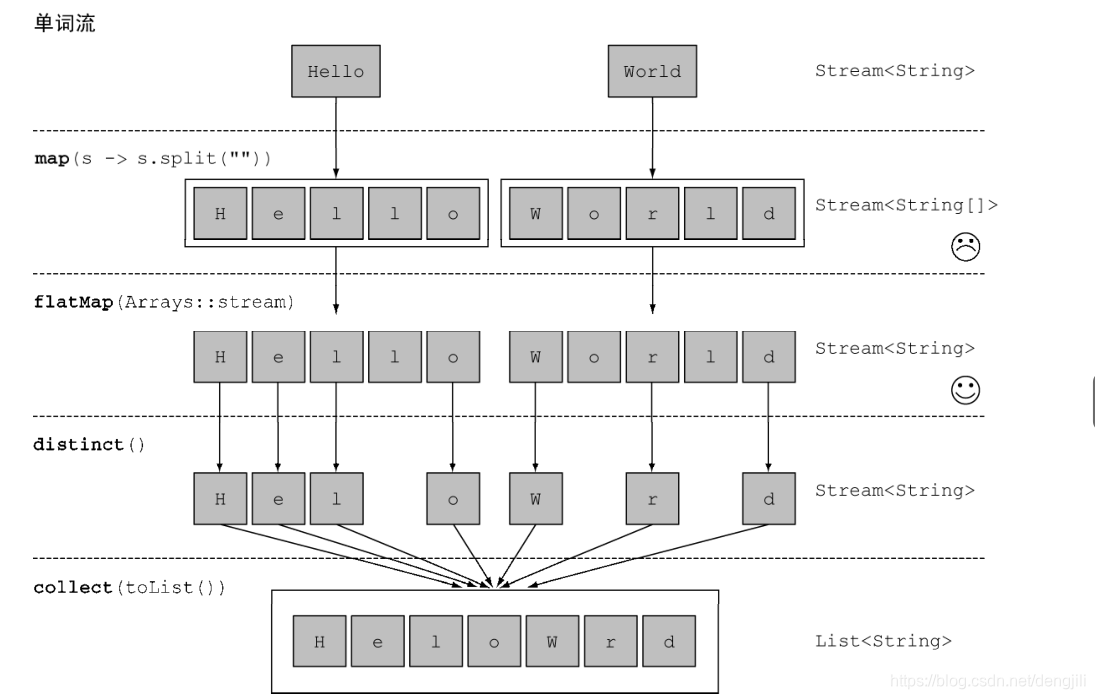
flatMap升维

给定两个数字列表，如何返回所有的数对呢？例如，给定列表[1, 2, 3]和列表[3, 4]，应该返回[(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)]。

public class StreamInt {
	public static void main(String[] args) {
		List<Integer> numbers1 = Arrays.asList(1, 2, 3);
		List<Integer> numbers2 = Arrays.asList(3, 4);
		// flatMap升维度
		List<int[]> pairs = numbers1.stream().flatMap(x -> numbers2.stream().map(y -> new int[] { x, y }))
				.collect(Collectors.toList());
		for (int[] pair : pairs) {
			System.out.println(Arrays.toString(pair));
		}
	}
}

测试结果：

[1, 3]
[1, 4]
[2, 3]
[2, 4]
[3, 3]
[3, 4]

这里是从一维升为二维，逻辑如下：

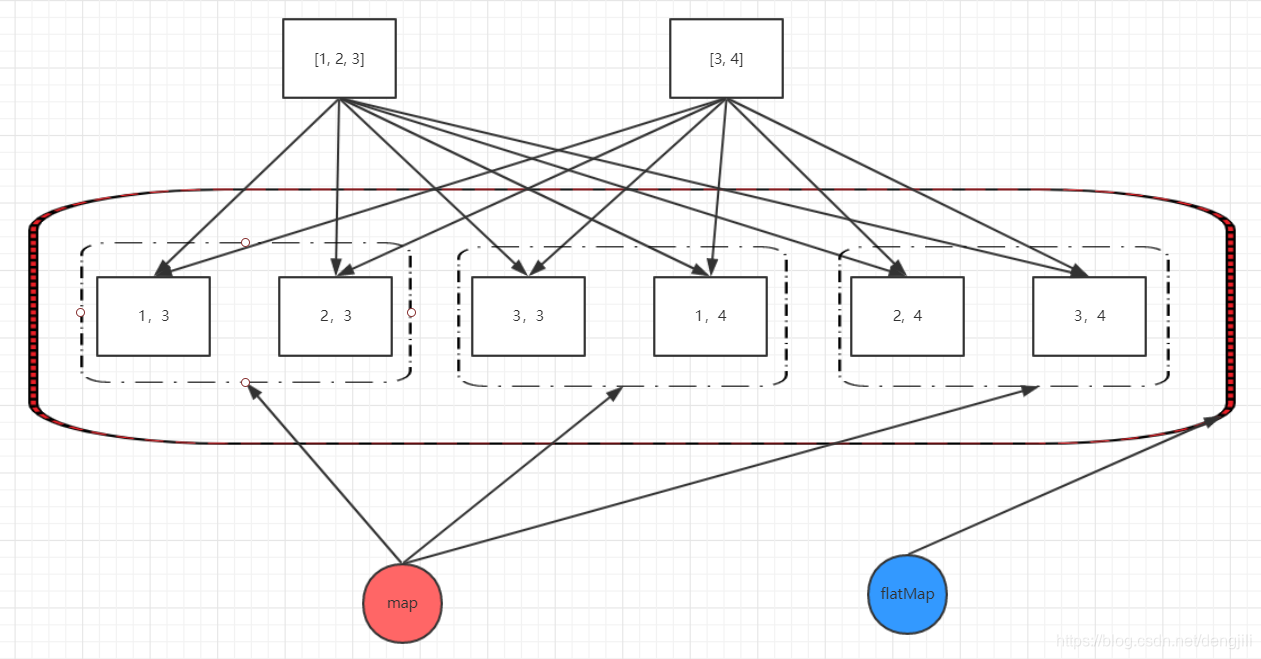
总结：flatMap将map结果归类，从而达到升降维目的