POJ2104 K-TH NUMBER 传说中的主席树

题意：给出1e5个数，向你提5000问，L到R间的第K个数是多少？

————————————————————————————————————————————————————————

这个题着实没有其它很好的办法，是主席树的经典题目。

主席树，又叫可持久化线段树或者函数式线段树。我只知道这些了，据说是一位大神没学会划分树就自己搞了这么个替代品，结果，比原来的还要强。哎~，真不知道这群大神的脑子是咋整的，膜拜吧！

本人水平有限，这是我见过的最神奇的数据结构了，感觉比伸展树、熟练剖分神奇多了，鼓捣了大半天才明白其中的原理。

说一下思路：

因为是求第k大的数，所以线段树是不行的，因为数是排好序的，所以伸展树好像也不好解决。

所以主席树用到了前缀和的思想，如果知道每个数在L前出现了几次，R前出现了几次，做差就可以在L~R间出现了几次，自然也就知道k大了！

所以，第一步把所有的数排序、去重。

数列：2 4 6 8 8 6 4 2

hash:2 4 6 8

数列变为：1 2 3 4 4 3 2 1（就是各个数在hash中的排序）

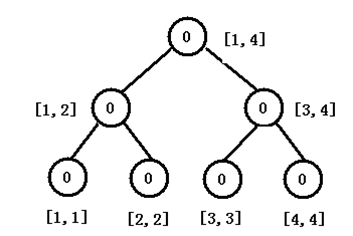
第二部建n+1个线段树，就是按照数列的顺序每读入一个数就建一个线段树，把新树在上一颗树的基础上把这个数字按照去重后的排序加入当前线段树。

这样求L~R的k值就用线段树R减去线段树L-1，在差中找k大值就可以了。

......

出现的问题：超空间

这个事大神替我们想到了，那就是每一个线段树与上一个线段树只有一条路径（根到叶）不同，所以，新树除了这条路径外所有节点都用上一个线段树的。

这样空间为第一颗线段树(4*n）+每个数字一条链（n*logn）

代码敲了1天多，主要是本人习惯于用指针和new，但是这次点太多，超时了。没办法只好给出数组模拟指针。ok!

网上有人说可以一次性malloc多个，这样可以省时通过，没来得及试，不过应该可以，但是就没有了指针+new的灵活性，不做也罢。

但是没舍得把指针的丢掉，这个理解起来清楚容易，哎~，就这麽着吧！

————————————————————————————————————————————————————————

数组版：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>

 using namespace std;
 const int maxn=;
 const int maxnn=;
 int root[maxn],ls[maxnn],rs[maxnn],cnt[maxnn],tot;
 int sz[maxn],hash[maxn];
 void build(int &cur,int l,int r)
 {
     cur=tot++;
     cnt[cur]=;
     if(l!=r)
     {
         int mid=(l+r)/;
         build(ls[cur],l,mid);
         build(rs[cur],mid+,r);
     }
 }
 void update(int pre,int ps,int &cur,int l,int r)
 {
     cur=tot++;
     cnt[cur]=cnt[pre]+;
     ls[cur]=ls[pre];rs[cur]=rs[pre];
     if(l==r)return ;
     int mid=(l+r)/;
     if(ps<=mid)update(ls[pre],ps,ls[cur],l,mid);
     else update(rs[pre],ps,rs[cur],mid+,r);
 }
 int query(int lt,int rt,int l,int r,int k)
 {
     if(l==r)return l;
     int mid=(l+r)/,cha=cnt[ls[rt]]-cnt[ls[lt]];
     if(k<=cha)return query(ls[lt],ls[rt],l,mid,k);
     else return query(rs[lt],rs[rt],mid+,r,k-cha);
 }
 int main()
 {
     int m,n,l,r,k;
     while(scanf("%d%d",&n,&m)==)
     {
         for(int i=;i<=n;++i)
         {
             scanf("%d",sz+i);
             hash[i]=sz[i];
         }
         sort(hash+,hash+n+);
         int siz=unique(hash+,hash++n)-hash-;
         for(int i=;i<=n;++i)
             sz[i]=lower_bound(hash+,hash++siz,sz[i])-hash;
         tot=;
         build(root[],,siz);
         for(int i=;i<=n;++i)
             update(root[i-],sz[i],root[i],,siz);
         while(m--)
         {
             scanf("%d%d%d",&l,&r,&k);
             printf("%d\n",hash[query(root[l-],root[r],,siz,k)]);
         }
     }
     return ;
 } 

指针版（由于多次malloc，超时了）

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int maxn=;
 struct node
 {
     int cnt;
     node *ch[];
     int l,r;
 }* root[maxn];
 int n,mm,l,r,k;
 int sz[maxn],hash[maxn];

 void readint(int &x)
 {
     char c=getchar();
     int f=;
     for(;c<''||c>'';c=getchar())if(c=='-')f=-f;
     x=;
     for(;c<=''&&c>='';c=getchar())x=x*+c-'';
     x=x*f;
 }
 void build(node * &cur,int l,int r)
 {
     cur=(node *)malloc(sizeof(node));
     cur->cnt=;
     cur->ch[]=cur->ch[]=NULL;
     cur->l=l;cur->r=r;
     if(l!=r)
     {
         int mid=(l+r)/;
         build(cur->ch[],l,mid);
         build(cur->ch[],mid+,r);
     }
 }
 void update(node * pre,int ps,node * &cur,int l,int r)
 {
     cur=(node *)malloc(sizeof(node));
     cur->cnt=pre->cnt+;
     cur->l=pre->l;cur->r=pre->r;
     cur->ch[]=pre->ch[];
     cur->ch[]=pre->ch[];
     if(l==r)return ;
     int mid=(l+r)/;
     if(ps<=mid)update(pre->ch[],ps,cur->ch[],l,mid);
     else update(pre->ch[],ps,cur->ch[],mid+,r);
 }
 int query(node * lt,node *rt,int l,int r,int k)
 {
     if(l==r)return l;
     int mid=(l+r)/,cha=rt->ch[]->cnt - lt->ch[]->cnt;
     if(k<=cha)return query(lt->ch[],rt->ch[],l,mid,k);
     else return query(lt->ch[],rt->ch[],mid+,r,k-cha);
 }
 int main()
 {
     while(scanf("%d%d",&n,&mm)==)
     {
         for(int i=;i<=n;++i)
         {
             readint(sz[i]);
             hash[i]=sz[i];
         }
         sort(hash+,hash+n+);
         int siz=unique(hash+,hash+n+)-hash-;
         for(int i=;i<=n;++i)
             sz[i]=lower_bound(hash+,hash+siz+,sz[i])-hash;
         build(root[],,siz);
         for(int i=;i<=n;++i)
             update(root[i-],sz[i],root[i],,siz);
         while(mm--)
         {
             readint(l);readint(r);readint(k);
             printf("%d\n",hash[query(root[l-],root[r],,siz,k)]);
         }
     }
     return ;
 }