网络流24题 gay题报告
洛谷上面有一整套题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 extra
①飞行员配对方案问题。top
裸二分图匹配。
#include <cstdio>
const int N = , M = ;
struct Edge {
int nex, v;
}edge[M << ]; int top;
int n, m, e[N], mat[N], vis[N], Time;
inline void add(int x, int y) {
top++;
edge[top].v = y;
edge[top].nex = e[x];
e[x] = top;
return;
}
bool DFS(int x) {
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(vis[y] == Time) {
continue;
}
vis[y] = Time;
if(!mat[y] || DFS(mat[y])) {
mat[y] = x;
return ;
}
}
return ;
}
int main() {
scanf("%d%d", &m, &n);
int x, y;
while(scanf("%d%d", &x, &y)) {
if(x == - && y == -) {
break;
}
add(x, y);
add(y, x);
}
int ans = ;
for(int i = ; i <= m; i++) {
Time = i;
if(DFS(i)) {
ans++;
}
}
if(!ans) {
printf("No Solution!");
return ;
}
printf("%d\n", ans);
for(int i = m + ; i <= n; i++) {
if(mat[i]) {
printf("%d %d", mat[i], i);
ans--;
if(ans) {
puts("");
}
}
}
return ;
}
匈牙利AC代码
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N];
std::queue<int> Q; inline void add(int x, int y, int z) {
top++;
edge[top].nex = e[x];
edge[top].v = y;
edge[top].c = z;
e[x] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c && d[y] == INF) {
d[y] = d[x] + ;
Q.push(y);
}
}
}
return d[t] < INF;
} int DFS(int x, int t, int maxF) {
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(d[x] + != d[y] || !edge[i].c) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
return ans;
}
}
return ans;
} int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} int main() {
int n, m;
scanf("%d%d", &m, &n);
int x, y;
while(scanf("%d%d", &x, &y)) {
if(x == -) {
break;
}
add(x, y, );
add(y, x, );
//printf("%d %d \n", x, y);
}
int s = n + , t = n + ;
for(int i = ; i <= m; i++) {
add(s, i, );
add(i, s, );
//printf("s %d \n", i);
}
for(int i = m + ; i <= n; i++) {
add(i, t, );
add(t, i, );
//printf("%d t \n", i);
} int ans = solve(s, t);
if(!ans) {
printf("No Solution!");
return ;
}
printf("%d\n", ans);
for(int i = ; i <= top; i += ) {
if(edge[i].c || edge[i ^ ].v == s || edge[i].v == t) {
continue;
}
printf("%d %d", edge[i ^ ].v, edge[i].v);
ans--;
if(ans) {
puts("");
}
} return ;
}
DinicAC代码
②负载平衡问题。top
环形均分纸牌。也可以用费用流做。
首先每个人的牌数是sum/n，这点可以建立源汇，用流量来控制。
所以代价交换次数最小就用费用来控制。
相邻之间连边，费用为1，流量INF。
每个点与源连边，流量为一开始的牌数，费用为0。
每个点与汇连边，流量为sum/n，费用为0。
然后跑最小费用最大流。
(这里注意，无向边费用流，对于一条边要建4条边才行。
最大流可以只建两条边，流量都为c，但是费用流的费用要取负，不好搞。)
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top = ; int e[N], d[N], pre[N], Time, flow[N];
std::queue<int> Q;
bool vis[M]; inline void add(int x, int y, int z, int w) {
top++;
edge[top].nex = e[x];
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
continue;
}
if(d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
pre[y] = i;
flow[y] = std::min(flow[x], edge[i].c);
//printf("y = %d d = %d flow = %d \n", y, d[y], flow[y]);
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
/*for(int i = 1; i <= 7; i++) {
printf("%d %d \n", d[i], flow[i]);
}*/
return d[t] < INF; // error 0
} inline void update(int s, int t) {
int f = flow[t], i = pre[t];
while(t != s) {
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
return;
} int solve(int s, int t, int &cost) {
int ans = ;
cost = ;
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
//printf("%d %d \n", ans, cost);
}
return ans;
} int main() {
int n, sum = ;
scanf("%d", &n);
int s = n + , t = n + ;
for(int i = , x; i <= n; i++) {
scanf("%d", &x);
sum += x;
if(i > ) {
add(i, i - , INF, );
}
if(i < n) {
add(i, i + , INF, );
}
add(s, i, x, );
}
add(, n, INF, );
add(n, , INF, );
sum /= n;
for(int i = ; i <= n; i++) {
add(i, t, sum, );
} int ans, cost;
ans = solve(s, t, cost);
printf("%d", cost);
return ;
}
AC代码
③软件补丁问题。top
٩(๑>◡<๑)۶
这题看了一会，想到一个状压+SPFA转移的做法，算一下复杂度好像不行，但是没有别的算法了....
跑去看题解，还真是？？！！
弃疗了。
④魔术球问题。top
这题，我有个非常SB的二分费用流！
然后果断T掉......
没事，我会动态加点！然后加出负环来了...GG。
负环如下：
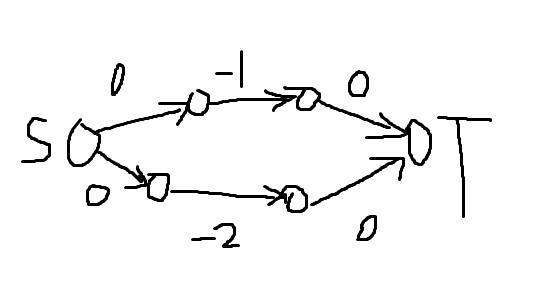
图中所有流量为1，数字表示费用。先加上面三条边，然后跑一遍，然后加下面三条边再跑。
可以发现此时出现了流量为1的负环.......
然后跑去看题解，嗯？？？最小路径覆盖？(我傻了。)
然后根据题解的启示，回想小凯的疑惑，用找规律A了......
讲一下我的SB费用流。
我们发现点数不好一开始确定，进而想到二分。
然后如何判定呢？
首先建图，如果和为完全平方数，就小->大连边。
源汇往每个点连边。
这样的话，可以用一条流量表示一个柱子，源点限流n，球限流1。但是发现一个问题：每个点都有一条路径为源->该点->汇。这样不是没有意义了吗？
不！我们可以求最大费用啊！那么就可以让你经过尽量多的球了。
所以每个球内部的那条边，费用为负编号。别的费用都为0。
观察最大费用是否为∑i即可。
输出方案就是先搜索源点的出边，找到满流的为起点。
然后枚举每一条边，把每个节点的后继找到。然后就可以输出了。
正确的做法：发现其实就是最小路径覆盖......;
还是二分，然后看最小路径覆盖是不是等于n。
(还有人用搜索过...)
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top; int e[N], d[N], pre[N], flow[N], vis[N], Time, n, ss;
std::queue<int> Q;
bool sqr[N]; inline void add(int x, int y, int z, int w) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c && d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
flow[y] = std::min(flow[x], edge[i].c);
pre[y] = i;
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
return d[t] < INF;
} inline void update(int s, int t) {
int f = flow[t];
int i = pre[t];
while(s != t) {
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
return;
} inline int solve(int s, int t, int &cost) {
int ans = ;
cost = ;
Time = ;
memset(vis, , sizeof(vis));
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
}
return ans;
} inline bool check(int k) {
//printf("k = %d \n", k);
memset(e, , sizeof(e));
top = ;
int s = k + k + , t = k + k + ;
ss = k + k + ;
add(s, ss, n, );
for(int i = ; i <= k; i++) {
add(i, i + k, , -i);
add(ss, i, , );
add(i + k, t, , );
}
for(int i = ; i < k; i++) {
for(int j = i + ; j <= k; j++) {
if(sqr[i + j]) {
add(i + k, j, , );
}
}
}
int cost;
solve(s, t, cost);
//printf("max cost = %d \n", -cost);
return cost + (k + ) * k / == ;
} int main() {
for(int i = ; i <= ; i++) {
sqr[i * i] = ;
}
scanf("%d", &n);
int l = n, r = ;
if(l > ) {
l <<= ;
}
while(l < r) {
int mid = (l + r + ) >> ;
if(check(mid)) {
l = mid;
}
else {
r = mid - ;
}
}
check(r);
printf("%d\n", r);
std::priority_queue<int, std::vector<int>, std::greater<int> > P;
for(int i = e[ss]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
P.push(y);
}
}
memset(pre, , sizeof(pre));
for(int i = ; i <= top; i += ) {
int y = edge[i].v;
int x = edge[i ^ ].v;
if(!edge[i].c && r < x && x <= r * && y <= r && x - r < y) {
pre[x - r] = y; }
} while(!P.empty()) {
int x = P.top();
P.pop();
while(x) {
printf("%d ", x);
x = pre[x];
}
puts("");
} return ;
}
费用流二分TLE
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top; int e[N], d[N], pre[N], flow[N], vis[N], Time, n, ss;
std::queue<int> Q;
bool sqr[N]; inline void add(int x, int y, int z, int w) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c && d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
flow[y] = std::min(flow[x], edge[i].c);
pre[y] = i;
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
return d[t] < INF;
} inline void update(int s, int t) {
int f = flow[t];
int i = pre[t];
while(s != t) {
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
return;
} inline int solve(int s, int t, int &cost) {
int ans = ;
cost = ;
Time = ;
memset(vis, , sizeof(vis));
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
}
return ans;
} inline bool check(int k) {
//printf("k = %d \n", k);
memset(e, , sizeof(e));
top = ;
int s = k + k + , t = k + k + ;
ss = k + k + ;
add(s, ss, n, );
for(int i = ; i <= k; i++) {
add(i, i + k, , -i);
add(ss, i, , );
add(i + k, t, , );
}
for(int i = ; i < k; i++) {
for(int j = i + ; j <= k; j++) {
if(sqr[i + j]) {
add(i + k, j, , );
}
}
}
int cost;
solve(s, t, cost);
//printf("max cost = %d \n", -cost);
return cost + (k + ) * k / == ;
} int main() {
for(int i = ; i <= ; i++) {
sqr[i * i] = ;
}
scanf("%d", &n);
int r;
if((n & ) == ) {
r = n * (n / + ) - ;
}
else {
r = (n + ) * (n + ) / - ;
}
check(r);
printf("%d\n", r);
std::priority_queue<int, std::vector<int>, std::greater<int> > P;
for(int i = e[ss]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
P.push(y);
}
}
memset(pre, , sizeof(pre));
for(int i = ; i <= top; i += ) {
int y = edge[i].v;
int x = edge[i ^ ].v;
if(!edge[i].c && r < x && x <= r * && y <= r && x - r < y) {
pre[x - r] = y; }
} while(!P.empty()) {
int x = P.top();
P.pop();
while(x) {
printf("%d ", x);
x = pre[x];
}
puts("");
} return ;
}
费用流AC代码
⑤孤岛营救问题。top
sjf天天在那说什么拯救大兵瑞恩，有心理阴影了，告辞。
最后还是写了......
因为之前的某个契机，一直在想枚举拿哪个钥匙。
后来思路陡然开阔，反正边权都为1，不就是状压BFS吗???
然后想着写个主程序就走，写了一半发现好像比较好写，就把读入和预处理也写了，然后就完美的避开了所有坑一A了...
#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm> const int INF = 0x3f3f3f3f, N = ;
const int dx[] = {, , , -};
const int dy[] = {, -, , }; struct Node {
int x, y, s;
Node(int X, int Y, int S) {
x = X;
y = Y;
s = S;
}
}; int G[N][N], d[N][N][], line[N][N], row[N][N], vis[N][N][];
std::queue<Node> Q;
int n, m, p; inline bool valid(int x, int y, int s, int i) {
if(i < ) { // row
y = std::min(y, y + dy[i]);
if(row[x][y] == -) {
return ;
}
return (s | row[x][y]) == s;
}
else { // line
x = std::min(x, x + dx[i]);
if(line[x][y] == -) {
return ;
}
return (s | line[x][y]) == s;
}
} inline void BFS() {
memset(d, 0x3f, sizeof(d));
d[][][G[][]] = ;
vis[][][G[][]] = ;
Q.push(Node(, , G[][]));
while(!Q.empty()) {
int x = Q.front().x;
int y = Q.front().y;
int s = Q.front().s;
Q.pop();
for(int i = ; i < ; i++) {
if(!valid(x, y, s, i)) {
continue;
}
int tx = x + dx[i];
int ty = y + dy[i];
int ts = s | G[tx][ty];
if(vis[tx][ty][ts]) {
continue;
}
d[tx][ty][ts] = d[x][y][s] + ;
vis[tx][ty][ts] = ;
Q.push(Node(tx, ty, ts));
}
} return;
} int main() {
scanf("%d%d%d", &n, &m, &p);
int k, A, B, C, D, E;
scanf("%d", &k);
for(int i = ; i <= k; i++) {
scanf("%d%d%d%d%d", &A, &B, &C, &D, &E);
if(A > C) {
std::swap(A, C);
std::swap(B, D);
}
if(B > D) {
std::swap(A, C);
std::swap(B, D);
}
if(A == C) {
row[A][B] = E ? ( << (E - )) : -;
}
else if(B == D) {
line[A][B] = E ? ( << (E - )) : -;
}
}
int s;
scanf("%d", &s);
for(int i = ; i <= s; i++) {
scanf("%d%d%d", &A, &B, &E);
G[A][B] |= ( << (E - ));
}
for(int i = ; i <= n; i++) {
row[i][] = row[i][m] = -;
}
for(int i = ; i <= m; i++) {
line[][i] = line[n][i] = -;
}
BFS();
int ans = INF;
for(int i = ; i < ( << p); i++) {
ans = std::min(ans, d[n][m][i]);
}
if(ans == INF) {
ans = -;
}
printf("%d", ans);
return ;
}
AC代码
⑥圆桌问题。top
本人多次将m, n打错...
每张桌子上每组人不能超过1个。
通过限制流量为1来实现。
源点向组连流量为人数的边，桌子向汇点连流量为可容纳人数的边。
桌子和组之间两两连流量为1的边。
如果最大流小于总人数，就不合法。
方案就是每组的满流出边代表的桌子。
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>
// #define id(i, j) (((i) - 1) * m + (j)) const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N];
std::queue<int> Q; inline void add(int x, int y, int z) {
//printf("add : %d %d \n", x, y); top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} int main() {
int n, m, sum = ;
scanf("%d%d", &m, &n);
int s = n + m + , t = n + m + ;
for(int i = , x; i <= m; i++) {
scanf("%d", &x);
add(s, i, x);
sum += x;
}
for(int i = , x; i <= n; i++) {
scanf("%d", &x);
add(m + i, t, x);
for(int j = ; j <= m; j++) {
add(j, m + i, );
}
} if(solve(s, t) != sum) {
puts("");
return ;
}
puts(""); for(int x = ; x <= m; x++) {
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c || y == s) {
continue;
}
printf("%d ", y - m);
}
puts("");
} return ;
}
AC代码
⑦汽车加油行驶问题。top
这TM是最短路啊......
我一开始发现比较复杂，然后想着用费用流，只给一个流量，然后发现这不就是最短路吗...
具体来说，因为只能走k步比较难处理，就一次性把这k步全走了好了......
关于强制消费：看这个样例。
7 5 4 5 100
0 0 0 0 0 0 0
0 0 0 0 0 0 0
1 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 1 1 1 1 0 0
嗯，可以发现最优路线要在最底下进行绕路......
这启示我们用BFS来连边。
然后就被这个神逻辑题给烦死了......
看代码了。
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring> const int N = , M = , INF = 0x3f3f3f3f;
const int dx[] = {, , , -};
const int dy[] = {, , -, }; struct Edge {
int nex, v, len;
}edge[M << ]; int top; struct Node {
int x, d;
Node(int X, int D) {
x = X;
d = D;
}
inline bool operator <(const Node &w) const {
return d > w.d;
}
}; struct POI {
int x, y, d, dist;
POI(int X, int Y, int D, int T) {
x = X;
y = Y;
d = D;
dist = T;
}
}; int e[N], dis[N], vis[N], n, B, G[][], use[][];
std::priority_queue<Node> Q;
std::queue<POI> P; inline void add(int x, int y, int z) {
top++;
edge[top].v = y;
edge[top].len = z;
edge[top].nex = e[x];
e[x] = top;
return;
} inline void dijkstra(int s) {
memset(dis, 0x3f, sizeof(dis));
dis[s] = ;
Q.push(Node(s, ));
while(!Q.empty()) {
int x = Q.top().x;
if(vis[x] || dis[x] != Q.top().d) {
Q.pop();
continue;
}
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!vis[y] && dis[y] > dis[x] + edge[i].len) {
dis[y] = dis[x] + edge[i].len;
/*if(y == 21) {
printf("x = %d y = %d d[y] = %d \n", x, y, dis[y]);
}*/
Q.push(Node(y, dis[y]));
}
}
}
return;
} inline int cal(int i, int j, int a, int b) {
//printf("cal : (%d %d) -> (%d %d) %d \n", i, j, a, b, B * (std::max(0, i - a) + std::max(0, j - b)));
/*if(i == 1 && j == 2 && a == 1 && b == 1) {
printf("fds ans = %d \n", B * (std::max(0, i - a) + std::max(0, j - b)));
}*/
return B * (std::max(, i - a) + std::max(, j - b));
} inline int id(int x, int y) {
return (x - ) * n + y;
} int main() {
int K, A, c;
scanf("%d%d%d%d%d", &n, &K, &A, &B, &c);
int lm = n * n;
for(int i = ; i <= n; i++) {
for(int j = ; j <= n; j++) {
scanf("%d", &use[i][j]);
}
}
for(int i = ; i <= n; i++) {
for(int j = , f; j <= n; j++) {
int T = id(i, j);
add(T, T + lm, use[i][j] ? A : A + c);
G[i][j] = T;
P.push(POI(i, j, , ));
while(!P.empty()) {
int x = P.front().x;
int y = P.front().y;
int d = P.front().d;
int dist = P.front().dist;
P.pop();
for(int k = ; k < ; k++) {
int tx = x + dx[k];
int ty = y + dy[k];
if(tx && ty && tx <= n && ty <= n && G[tx][ty] != T) {
add(T + lm, id(tx, ty), dist + ((k > ) ? B : ));
G[tx][ty] = T;
//printf("%d %d = %d %d d = %d \n", i, j, tx, ty, d);
if(d < K && !use[tx][ty]) {
P.push(POI(tx, ty, d + , dist + ((k > ) ? B : )));
}
}
}
}
}
} dijkstra(id(, ) + lm); printf("%d", dis[id(n, n)]);
/*int x, y;
while(scanf("%d%d", &x, &y)) {
printf("%d \n", dis[id(x, y)]);
}*/
return ;
}
AC代码
⑧分配问题。top
源点向人连边，人和工作之间n²连边，工作向汇点连边。
最大/小费用最大流。
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top = ; int e[N], d[N], pre[N], Time, flow[N], G[N][N];
std::queue<int> Q;
bool vis[M]; inline void add(int x, int y, int z, int w) {
top++;
edge[top].nex = e[x];
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
continue;
}
if(d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
pre[y] = i;
flow[y] = std::min(flow[x], edge[i].c);
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
return d[t] < INF; // error 0
} inline void update(int s, int t) {
int f = flow[t], i = pre[t];
while(t != s) {
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
return;
} int solve(int s, int t, int &cost) {
int ans = ;
cost = ;
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
}
return ans;
} int main() {
int n;
scanf("%d", &n);
int s = n << | , t = (n + ) << ;
for(int i = ; i <= n; i++) {
for(int j = ; j <= n; j++) {
int x;
scanf("%d", &G[i][j]);
add(i, n + j, , G[i][j]);
}
add(s, i, , );
add(n + i, t, , );
} int cost;
solve(s, t, cost);
printf("%d\n", cost); memset(vis, , sizeof(vis));
int temp = ;
for(int i = ; i <= n; i++) {
for(int j = ; j <= n; j++) {
edge[++temp].c = ;
edge[temp].len = -G[i][j];
edge[++temp].c = ;
edge[temp].len = G[i][j];
}
edge[++temp].c = ;
edge[++temp].c = ;
edge[++temp].c = ;
edge[++temp].c = ;
} solve(s, t, cost);
printf("%d", -cost); return ;
}
AC代码
⑨试题库问题。top
每个种类建点，每个试题建点。
源点向种类连流量为需求量的边，试题向汇点连流量为1的边。
试题和能匹配的种类之间连流量为1的边。
然后跑最大流。如果小于总需求量就无解。
方案就是每个种类出去的满流的边。
有个坑：当某一种类需求量为0的时候我的写法会输出源点。解决办法是不加那一条边。
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>
// #define id(i, j) (((i) - 1) * m + (j)) const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N], G[][];
std::queue<int> Q; inline void add(int x, int y, int z) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} int main() {
int n, k, sum = ;
scanf("%d%d", &k, &n);
int s = n + k + , t = n + k + ;
for(int i = , x; i <= k; i++) {
scanf("%d", &x);
if(x) {
add(s, i, x);
}
sum += x;
}
for(int i = , x, y; i <= n; i++) {
scanf("%d", &y);
for(int j = ; j <= y; j++) {
scanf("%d", &x);
add(x, k + i, );
}
add(k + i, t, );
} if(solve(s, t) != sum) {
printf("No Solution!");
return ;
} for(int a = ; a <= k; a++) {
printf("%d: ", a);
for(int i = e[a]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c) {
continue;
}
printf("%d ", y - k);
}
puts("");
} return ;
}
AC代码
⑩运输问题。top
跟T8差不多吧......
#include <cstdio>
#include <cstring>
#include <queue> const int INF = 0x3f3f3f3f; struct EK {
struct Edge {
int v, nex, f, len;
inline void cl() {
v = nex = f = len = ;
return;
}
}edge[ * * + ]; int top;
int e[], dis[], pre[], flow[], vis[];
EK() {
top = ;
}
inline void clear() {
for(int i = ; i <= top; i++) {
edge[i].cl();
}
top = ;
memset(pre, , sizeof(pre));
memset(dis, , sizeof(dis));
memset(vis, , sizeof(vis));
memset(flow, , sizeof(flow));
memset(e, , sizeof(e));
return;
}
inline void add(int x, int y, int z, int l) {
top++;
edge[top].v = y;
edge[top].f = z;
edge[top].len = l;
edge[top].nex = e[x];
e[x] = top++;
edge[top].v = x;
edge[top].f = ;
edge[top].len = -l;
edge[top].nex = e[y];
e[y] = top;
return;
}
inline bool SPFA(int s, int t) {
memset(dis, 0x3f, sizeof(dis));
memset(vis, , sizeof(vis));
std::queue<int> Q;
Q.push(s);
vis[s] = ;
dis[s] = ;
flow[s] = INF;
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].f && dis[y] > dis[x] + edge[i].len) {
dis[y] = dis[x] + edge[i].len;
pre[y] = i;
flow[y] = std::min(flow[x], edge[i].f);
if(vis[y]) {
continue;
}
vis[y] = ;
Q.push(y);
}
}
}
return dis[t] < INF;
}
inline void update(int s, int t) {
int p = t;
while(p != s) {
int i = pre[p];
edge[i].f -= flow[t];
edge[i ^ ].f += flow[t];
p = edge[i ^ ].v;
}
return;
}
inline void solve(int s, int t, int &maxF, int &cost) {
maxF = cost = ;
while(SPFA(s, t)) {
maxF += flow[t];
cost += flow[t] * dis[t];
//printf("%d %d\n", flow[t], dis[t]);
update(s, t);
}
return;
}
}ek; int G[][], a[], b[]; int main() {
int m, n;
scanf("%d%d", &n, &m);
for(int i = ; i <= n; i++) {
scanf("%d", &a[i]);
}
for(int i = ; i <= m; i++) {
scanf("%d", &b[i]);
}
for(int i = ; i <= n; i++) {
for(int j = ; j <= m; j++) {
scanf("%d", &G[i][j]);
}
} int S = n + m + , T = n + m + ; for(int i = ; i <= n; i++) {
ek.add(S, i, a[i], );
}
for(int i = ; i <= m; i++) {
ek.add(n + i, T, b[i], );
}
for(int i = ; i <= n; i++) {
for(int j = ; j <= m; j++) {
ek.add(i, n + j, INF, G[i][j]);
}
} int c, d;
ek.solve(S, T, c, d);
printf("%d\n", d); ek.clear();
for(int i = ; i <= n; i++) {
ek.add(S, i, a[i], );
}
for(int i = ; i <= m; i++) {
ek.add(n + i, T, b[i], );
}
for(int i = ; i <= n; i++) {
for(int j = ; j <= m; j++) {
ek.add(i, n + j, INF, -G[i][j]);
}
} ek.solve(S, T, c, d);
printf("%d", -d); return ;
}
AC代码
①①太空飞行计划问题。top
另写了篇博客。
①②最小路径覆盖问题。top
模板题....
DAG最小路径覆盖数 = n - 转二分图后最大流
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N], vis[N], nex[N];
std::queue<int> Q; inline void add(int x, int y, int z) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
//printf("ans = %d \n", ans);
}
return ans;
} int main() {
int n, m;
scanf("%d%d", &n, &m);
for(int i = , x, y; i <= m; i++) {
scanf("%d%d", &x, &y);
add(x, y + n, );
}
int s = n + n + , t = n + n + ;
for(int i = ; i <= n; i++) {
add(s, i, );
add(n + i, t, );
} int ans = solve(s, t);
memset(vis, -, sizeof(vis));
for(int i = ; i <= (m << ); i += ) {
if(edge[i].c) {
continue;
}
//printf("chose %d -> %d \n", edge[i ^ 1].v, edge[i].v - n);
nex[edge[i ^ ].v] = edge[i].v - n;
vis[edge[i].v - n] = ;
} for(int i = ; i <= n; i++) {
if(vis[i]) {
int x = i;
while(x) {
printf("%d ", x);
x = nex[x];
}
puts("");
}
} printf("%d", n - ans);
return ;
}
AC代码
①③方格取数问题。top
二分图带权最大独立集 -> 二分图带权最小点覆盖。
做法是给每个点它的权值大小的流量，两部之间的流量为INF。
然后取最大流就是带权最小点覆盖。
可以感性理解一下：对于每一条边，两边一定有一个点满流，表示选择该点。严谨的证明不会...
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring>
#define id(i, j) (((i) - 1) * m + (j)) const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N], G[][];
std::queue<int> Q; inline void add(int x, int y, int z) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} int main() {
int n, m, sum = ;
scanf("%d%d", &n, &m);
int s = n * m + , t = n * m + ;
for(int i = ; i <= n; i++) {
for(int j = ; j <= m; j++) {
scanf("%d", &G[i][j]);
sum += G[i][j];
if((i + j) & ) {
add(s, id(i, j), G[i][j]);
}
else {
add(id(i, j), t, G[i][j]);
}
}
}
for(int i = ; i <= n; i++) {
for(int j = ; j <= m; j++) {
if(i < n) { // |
if((i + j) & ) {
add(id(i, j), id(i + , j), INF);
}
else {
add(id(i + , j), id(i, j), INF);
}
}
if(j < m) { // --
if((i + j) & ) {
add(id(i, j), id(i, j + ), INF);
}
else {
add(id(i, j + ), id(i, j), INF);
}
}
}
} printf("%d", sum - solve(s, t)); return ;
}
AC代码
①④最长k可重区间集问题。top
毒瘤...跟下面的17是一样的...17有个要注意的地方。
一开始受到下面15的启发，准备限制每个流的长度为k，发现不好控制最长。
一直在想怎么竖着流，期间想到过横着流但是没有深究...
两种建图方式，这里和17各自讲一种。
由于一个位置最多只能有k个区间，我们不妨把答案分成k层，用k个流量来模拟每一层。
有的位置不到k个怎么办？连额外的边引流。
具体来说，对于每两个彻底分离的区间，都连费用为0，流量为1的边表示它们可能在同一层。
每个区间内部限流为1，费用为自己的长度。
然后从起点流出k个流量，向每个区间连边表示它可能是起点。
每个区间向汇点连边表示它可能是终点。
大概长这样......
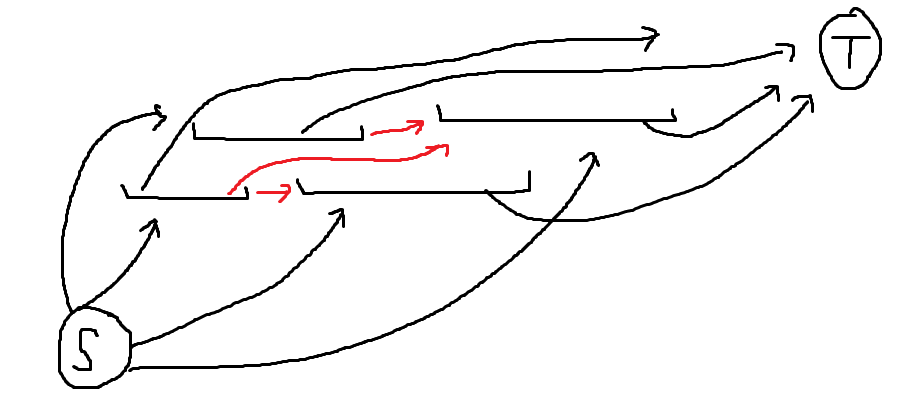
额外连一条s->t的边表示不到k个(不连也不会出问题)。
跑最大费用最大流即可。
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top = ; int e[N], d[N], pre[N], Time, flow[N], l[N], r[N];
std::queue<int> Q;
bool vis[M]; inline void add(int x, int y, int z, int w) {
top++;
edge[top].nex = e[x];
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
continue;
}
if(d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
pre[y] = i;
flow[y] = std::min(flow[x], edge[i].c);
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
return d[t] < INF; // error 0
} inline void update(int s, int t) {
int f = flow[t], i = pre[t];
//printf("update : ");
while(t != s) {
//printf("%d ", t);
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
//puts("");
return;
} int solve(int s, int t, int &cost) {
int ans = ;
cost = ;
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
}
return ans;
} int main() {
int n, k;
scanf("%d%d", &n, &k);
for(int i = ; i <= n; i++) {
scanf("%d%d", &l[i], &r[i]);
} int s = n * + , t = n * + , ss = n * + ;
for(int i = ; i <= n; i++) {
for(int j = ; j <= n; j++) {
if(r[i] <= l[j]) {
add(i + n, j, , );
//printf("add : %d %d \n", i, j);
}
}
add(i, i + n, , l[i] - r[i]);
add(s, i, , );
add(i + n, t, , );
}
add(ss, s, k, );
add(s, t, INF, );
int cost;
solve(ss, t, cost);
printf("%d", -cost); return ;
}
AC代码
①⑤最长不下降子序列问题。top
又是个毒瘤...首先第一问可以很轻易的用n² DP求出来，答案为s。
然后考虑我们要限制每条流量的长度为s，这搞鬼...？？
问了红太阳，他说把每个点拆成s个，然后每一层只向下一层连边。
然后跑最大流。不会出现一个点在不同的层数被使用多次的情况，因为i号点只能是序列中的第f[i]个，也就是f[i]层。
然后我们发现一个问题：这样建图会有500002个点，GG......
注意前面发现的一个东西：每个点只有在f[i]层有用，这样就可以把别的层都给去掉，点数缩减到了n。可过。
具体建图:
如果i < j && a[i] <= a[j] && f[i] + 1 == f[j]
连流量为1的边。
每个点限流为1。
源汇分别向f[i] == 1和f[i] == s连边，流量为1。
然后最大流就是第二问。
关于第三问：1和n可以用无限次。
要提到一个坑点就是要找的必须是下标不同的。所以样例不能一直取35，1 1也不能一直取1。
特判掉s == 1然后把1，n的限流改为INF，如果有源->1(一定有)就改为INF，如果有n->汇同理。
然后再来一次最大流。
注意：我的方法是把每条边的流量都重置，其实可以直接在残余网络上加边，跑出来的答案累加。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N], a[], f[], ans, n;
std::queue<int> Q; inline void add(int x, int y, int z) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
//printf("x = %d maxF = %d \n", x, maxF);
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} int main() { scanf("%d", &n);
for(int i = ; i <= n; i++) {
scanf("%d", &a[i]);
}
for(int i = ; i <= n; i++) {
for(int j = ; j < i; j++) {
if(a[i] >= a[j]) {
f[i] = std::max(f[i], f[j]);
}
}
f[i]++;
ans = std::max(ans, f[i]);
}
printf("%d\n", ans); int s = n << | ;
int t = s + ; for(int i = ; i <= n; i++) {
for(int j = i + ; j <= n; j++) {
if(a[i] <= a[j] && f[i] + == f[j]) {
add(i + n, j, );
}
}
add(i, i + n, );
if(f[i] == ) {
add(s, i, );
}
if(f[i] == ans) {
add(i + n, t, );
}
} printf("%d\n", solve(s, t)); if(ans == ) {
printf("%d", n);
return ;
} int temp = ;
for(int i = ; i <= n; i++) {
for(int j = i + ; j <= n; j++) {
if(a[i] <= a[j] && f[i] + == f[j]) {
edge[++temp].c = ;
edge[++temp].c = ;
}
}
bool flag = (i == || i == n);
edge[++temp].c = flag ? INF : ;
edge[++temp].c = ;
if(f[i] == ) {
edge[++temp].c = flag ? INF : ;
edge[++temp].c = ;
}
if(f[i] == ans) {
edge[++temp].c = flag ? INF : ;
edge[++temp].c = ;
}
} printf("%d", solve(s, t));
return ;
}
AC代码 重置流量
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N], a[], f[], ans, n;
std::queue<int> Q; inline void add(int x, int y, int z) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
//printf("x = %d maxF = %d \n", x, maxF);
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} int main() { //freopen("in.in", "r", stdin);
//freopen("my.out", "w", stdout); scanf("%d", &n);
for(int i = ; i <= n; i++) {
scanf("%d", &a[i]);
}
for(int i = ; i <= n; i++) {
for(int j = ; j < i; j++) {
if(a[i] >= a[j]) {
f[i] = std::max(f[i], f[j]);
}
}
f[i]++;
ans = std::max(ans, f[i]);
}
printf("%d\n", ans); int s = n << | ;
int t = s + ; for(int i = ; i <= n; i++) {
for(int j = i + ; j <= n; j++) {
if(a[i] <= a[j] && f[i] + == f[j]) {
add(i + n, j, );
}
}
add(i, i + n, );
if(f[i] == ) {
add(s, i, );
}
if(f[i] == ans) {
add(i + n, t, );
}
}
int r = solve(s, t);
printf("%d\n", r); if(ans == ) {
printf("%d", n);
return ;
}
add(s, , INF);
add(, n + , INF);
add(n, n + n ,INF);
if(f[n] == ans) {
add(n + n, t, INF);
} printf("%d", solve(s, t) + r);
return ;
}
AC代码 残余网络
①⑥骑士共存问题。top
首先想到行列连边，然后发现是马，就二分图了。
最大独立集 = n - 最大匹配。
有个坑点就是划分集合的时候，不能按照编号的奇偶性，例如2 * 2的棋盘，就是14一组，23一组。
要按照行+列的奇偶性。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; int e[N], d[N], n, m, G[][];
std::queue<int> Q; inline void add(int x, int y, int z) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
edge[i].c -= temp;
edge[i ^ ].c += temp;
ans += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} inline int id(int x, int y) {
return (x - ) * n + y;
} int main() {
int x, y;
scanf("%d%d", &n, &m);
for(int i = ; i <= m; i++) {
scanf("%d%d", &x, &y);
G[x][y] = ;
}
int s = n * n + , t = n * n + ;
for(int i = ; i < n; i++) {
for(int j = ; j <= n; j++) {
if(G[i][j]) {
continue;
}
int a = id(i, j);
bool f = (i + j) & ;
if(f) {
add(s, a, );
}
else {
add(a, t, );
}
//printf("x = %d %d \n", i, j);
if(j > && !G[i + ][j - ]) {
if(f) {
add(a, id(i + , j - ), );
}
else {
add(id(i + , j - ), a, );
}
//printf(" y = %d %d \n", i + 1, j - 2);
}
if(j > && i + < n && !G[i + ][j - ]) {
if(f) {
add(a, id(i + , j - ), );
}
else {
add(id(i + , j - ), a, );
}
//printf(" y = %d %d \n", i + 2, j - 1);
}
if(j + < n && !G[i + ][j + ]) {
if(f) {
add(a, id(i + , j + ), );
}
else {
add(id(i + , j + ), a, );
}
//printf(" y = %d %d \n", i + 1, j + 2);
}
if(j < n && i + < n && !G[i + ][j + ]) {
if(f) {
add(a, id(i + , j + ), );
}
else {
add(id(i + , j + ), a, );
}
//printf(" y = %d %d \n", i + 2, j - 1);
}
}
}
for(int j = ; j <= n; j++) {
if(!G[n][j]) {
int a = id(n, j);
if((n + j) & ) {
add(s, a, );
}
else {
add(a, t, );
}
}
} int ans = solve(s, t);
//printf("%d \n", ans); printf("%d", n * n - m - ans); return ;
}
AC代码
①⑦最长k可重线段集问题。top
上面14的带权版本。
新的建图方式：
还是用k个流量来模拟k层，一开始他们全在x轴上面流淌(什么沙雕动词...)，费用为0。
然后如果这里可以选一个线段，就分出去一个流量，表示这里有了一个线段。
具体来说，先把横坐标离散化，同时预处理出每个线段的长度。
先把x轴串成一串。然后对于每个线段，从左端点连到右端点，流量1，费用为长度，表示x轴上这一段可以选择用这个线段。
这里我们发现有个坑：线段可能与x轴垂直。
我一开始以为是交点个数不能超过k，于是直接continue了，后来发现题读错了，是相交线段个数。
怎么办呢？我们要自己向自己连边了？
拆点！！x轴每个位置拆成入点和出点，然后有垂直的就入点向出点连边即可。
大概长这样：
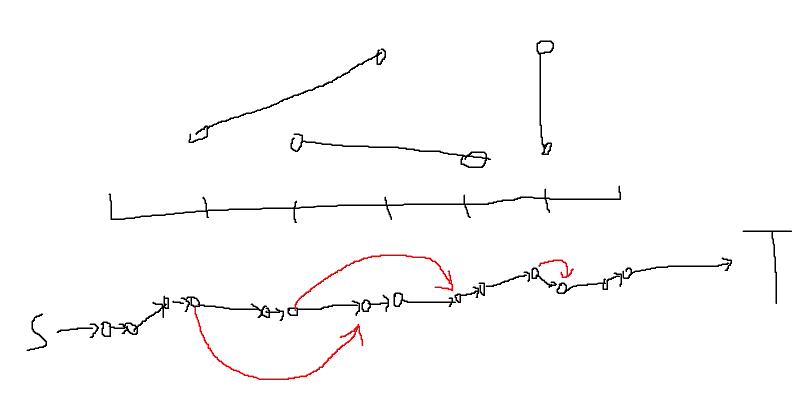
然后跑最大费用最大流即可。
听说坐标算距离那里会爆int...long long大法好(滑稽)
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
#include <cmath> typedef long long LL;
const int N = , M = ;
const LL INF = 0x3f3f3f3f3f3f3f3fll; struct Edge {
int nex, v, c;
LL len;
}edge[M << ]; int top = ; int e[N], pre[N], Time, flow[N], l[N], r[N], X[N];
LL d[N];
std::queue<int> Q;
bool vis[M];
LL lenth[N]; inline void add(int x, int y, int z, LL w) {
top++;
edge[top].nex = e[x];
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
continue;
}
if(d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
pre[y] = i;
flow[y] = std::min(flow[x], edge[i].c);
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
return d[t] < INF; // error 0
} inline void update(int s, int t) {
int f = flow[t], i = pre[t];
//printf("update : ");
while(t != s) {
//printf("%d ", t);
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
//puts("");
return;
} LL solve(int s, int t, LL &cost) {
int ans = ;
cost = ;
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
}
return ans;
} int main() {
int n, k, temp = ;
scanf("%d%d", &n, &k);
for(int i = , x, y; i <= n; i++) {
scanf("%d%d", &l[i], &x);
scanf("%d%d", &r[i], &y);
/*if(l[i] == r[i]) {
continue;
}*/
X[++temp] = l[i];
X[++temp] = r[i];
lenth[i] = (LL)(sqrt(1ll * (r[i] - l[i]) * (r[i] - l[i]) + 1ll * (y - x) * (y - x)));
} std::sort(X + , X + temp + );
temp = std::unique(X + , X + temp + ) - X - ; for(int i = ; i <= n; i++) {
l[i] = std::lower_bound(X + , X + temp + , l[i]) - X;
r[i] = std::lower_bound(X + , X + temp + , r[i]) - X;
if(l[i] == r[i]) {
add(l[i], l[i] + temp, , -lenth[i]);
continue;
}
add(l[i] + temp, r[i], , -lenth[i]);
}
for(int i = ; i < temp; i++) {
add(i + temp, i + , k, 0ll);
add(i, i + temp, k, 0ll);
}
add(temp, temp + temp, k, 0ll); int s = temp * + , ss = temp * + , t = temp * + ;
add(ss, s, k, );
add(s, , k, );
add(temp + temp, t, k, );
LL cost;
solve(ss, t, cost);
printf("%lld", -cost); return ;
}
AC代码
①⑧深海机器人问题。top
费用流。
只能取一次，解决方案是连一条1流量，有费用的边和一条INF流量，无费用的边。
源点向所有起点连边，所有终点向汇点连边。
然后跑最大费用最大流即可。
洛谷题面有个坑，横纵坐标没有反...
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top = ; int e[N], d[N], pre[N], Time, flow[N], n, m;
std::queue<int> Q;
bool vis[M]; inline void add(int x, int y, int z, int w) {
top++;
edge[top].nex = e[x];
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
continue;
}
if(d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
pre[y] = i;
flow[y] = std::min(flow[x], edge[i].c);
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
return d[t] < INF; // error 0
} inline void update(int s, int t) {
int f = flow[t], i = pre[t];
while(t != s) {
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
return;
} int solve(int s, int t, int &cost) {
int ans = ;
cost = ;
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
}
return ans;
} inline int id(int x, int y) {
return x * (m + ) + y + ;
} int main() { int a, b;
scanf("%d%d%d%d", &a, &b, &n, &m);
// q = m p = n
for(int i = ; i <= n; i++) {
for(int j = ; j < m; j++) {
int x;
scanf("%d", &x);
add(id(i, j), id(i, j + ), , -x);
add(id(i, j), id(i, j + ), INF, );
}
}
for(int j = ; j <= m; j++) {
for(int i = ; i < n; i++) {
int x;
scanf("%d", &x);
add(id(i, j), id(i + , j), , -x);
add(id(i, j), id(i + , j), INF, );
}
}
int S = (n + ) * (m + ) + ;
int T = S + ;
for(int i = , x, y, z; i <= a; i++) {
scanf("%d%d%d", &z, &x, &y);
add(S, id(x, y), z, );
}
for(int i = , x, y, z; i <= b; i++) {
scanf("%d%d%d", &z, &x, &y);
add(id(x, y), T, z, );
} int cost;
solve(S, T, cost);
printf("%d", -cost); return ;
}
AC代码
①⑨餐巾计划问题。top
我居然把一个点拆成了五个点！还A了...
首先想到，应该用流量来代表每天的餐巾，这样保证最大流就是保证每天有餐巾。
然后先来个最简单的模型吧。直接排成一排，从源点买，源点向每天连边，费用为购买的钱，不限流。每天向汇点连边，限流表示每天用的餐巾数。洗就是n²枚举后面的天数，与当前点连边，费用为洗的费用。
然后发现不行：你洗的话，一条餐巾就用了两次，这样总流量(买的总餐巾数)就比每天餐巾数之和少了。所以需要额外的流量来处理这个一巾多用的问题。
我有个很朴素的想法：再开一条流量，在连边的时候费用取负，把买的费用减去。
然后发现又挂了：你可能洗多次啊！每次洗都减，那还了得？
这启示我们第二次洗的时候不消除买的钱。
这就要把新买来的和之前洗过的分开处理。
然后我考虑了一会三个点，发现不行，就建了4个点，进来两个，出去两个。
还有个小问题，你洗的数量不可能超过你买的数量吧...因为我从源点那里买的时候流量为INF，所以就要在洗的时候限流。然后又多出来一个点...
到最后每个点拆成了5个点...虽然正确性没问题了但是...
你见过1w个点，n²条边的费用流吗...
大概长这样...
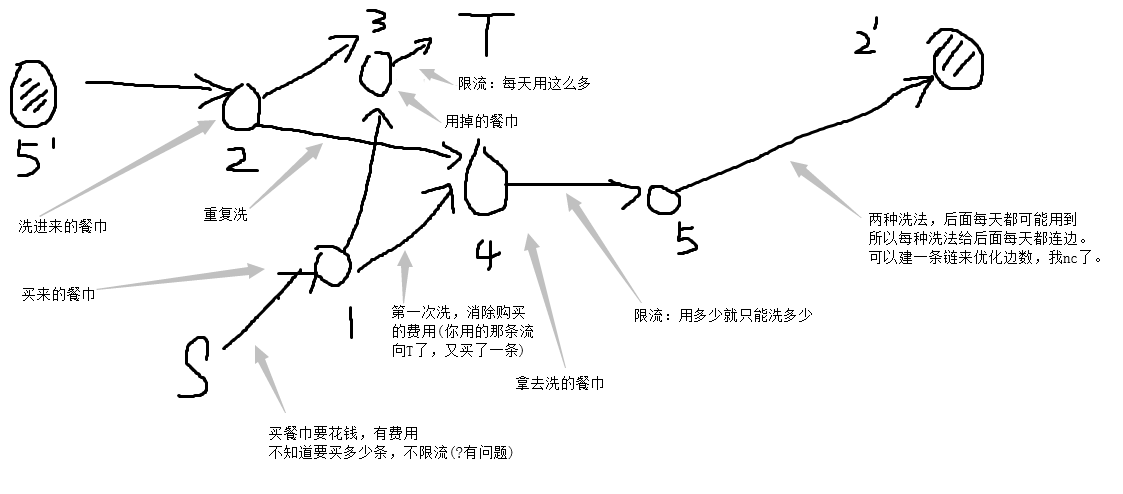
看起来比较恐怖......实测TLE，60分。
然后我优化连边一波，把n²连边改成每个5号点之间连流量INF，费用为0的链，就A了!!??
(虽然速度是正解的两倍...)
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring> typedef long long LL;
const int N = , M = ;
const LL INF = 0x3f3f3f3f3f3f3f3fll; struct Edge {
int nex, v;
LL len, c;
}edge[M << ]; int top = ; int e[N], pre[N], vis[N], Time;
LL d[N], flow[N], use[N];
std::queue<int> Q; inline void add(int x, int y, LL z, LL w) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
//printf("%lld \n%lld \n\n", d[t], INF);
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
//printf("d[%d] = %lld \n", x, d[x]);
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c && d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
flow[y] = std::min(flow[x], edge[i].c);
pre[y] = i;
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
//printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
return d[t] < INF;
} inline void update(int s, int t) {
LL f = flow[t];
//printf("update : f = %lld \n", f);
while(s != t) {
//printf("t = %d \n", t);
int i = pre[t];
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
}
return;
} inline LL solve(int s, int t, LL &cost) {
LL ans = ;
cost = ;
memset(vis, , sizeof(vis));
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
//printf("f = %lld d = %lld \n", flow[t], d[t]);
//printf("cost = %lld \n", cost);
update(s, t);
Time++;
}
return ans;
} int n;
inline int id(int i, int k) {
return (k - ) * n + i;
} int main() {
int quick, slow;
LL sc, buy, qc;
scanf("%d", &n);
int s = n * + , t = n * + ;
for(int i = ; i <= n; i++) {
scanf("%lld", &use[i]);
}
scanf("%lld%d%lld%d%lld", &buy, &quick, &qc, &slow, &sc); for(int i = ; i <= n; i++) {
add(s, i, INF, buy);
add(id(i, ), t, use[i], );
add(i, id(i, ), use[i], );
add(id(i, ), id(i, ), use[i], );
add(i, id(i, ), use[i], -buy);
add(id(i, ), id(i, ), use[i], );
add(id(i, ), id(i, ), use[i], );
/*for(int j = i + quick; j <= n; j++) {
add(id(i, 5), id(j, 2), INF, qc);
}
for(int j = i + slow; j <= n; j++) {
add(id(i, 5), id(j, 2), INF, sc);
}*/
if(i + quick <= n) {
add(id(i, ), id(i + quick, ), INF, qc);
}
if(i + slow <= n) {
add(id(i, ), id(i + slow, ), INF, sc);
}
if(i < n) {
add(id(i, ), id(i + , ), INF, );
}
} LL cost;
solve(s, t, cost);
printf("%lld", cost);
return ;
}
AC代码
接下来说正解：
这个题目都提醒我了，按照早晚拆点.....
然后，并非早->晚，而是S->晚->之后的早->T
S向晚连流量为当天餐巾数量的边，表示早上留下来的脏餐巾。
早向T连同样流量的边，表示今天用这么多。
S还要向早连收费的边，表示购买。
晚向后面的早连收费的边，表示洗。
晚向下一晚连INF，表示脏餐巾留着以后洗。
最后跑最小费用最大流即可。
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring> typedef long long LL;
const int N = , M = ;
const LL INF = 0x3f3f3f3f3f3f3f3fll; struct Edge {
int nex, v;
LL len, c;
}edge[M << ]; int top = ; int e[N], pre[N], vis[N], Time;
LL d[N], flow[N], use[N];
std::queue<int> Q; inline void add(int x, int y, LL z, LL w) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
//printf("%lld \n%lld \n\n", d[t], INF);
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
//printf("d[%d] = %lld \n", x, d[x]);
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c && d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
flow[y] = std::min(flow[x], edge[i].c);
pre[y] = i;
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
//printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
return d[t] < INF;
} inline void update(int s, int t) {
LL f = flow[t];
//printf("update : f = %lld \n", f);
while(s != t) {
//printf("t = %d \n", t);
int i = pre[t];
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
}
return;
} inline LL solve(int s, int t, LL &cost) {
LL ans = ;
cost = ;
memset(vis, , sizeof(vis));
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
//printf("f = %lld d = %lld \n", flow[t], d[t]);
//printf("cost = %lld \n", cost);
update(s, t);
Time++;
}
return ans;
} int n;
inline int id(int i, int k) {
return (k - ) * n + i;
} int main() {
int quick, slow;
LL sc, buy, qc;
scanf("%d", &n);
int s = n * + , t = n * + ;
for(int i = ; i <= n; i++) {
scanf("%lld", &use[i]);
}
scanf("%lld%d%lld%d%lld", &buy, &quick, &qc, &slow, &sc); for(int i = ; i <= n; i++) {
add(s, i, INF, buy);
add(s, n + i, use[i], );
add(i, t, use[i], );
if(i < n) {
add(n + i, n + i + , INF, );
}
if(i + quick <= n) {
add(n + i, i + quick, INF, qc);
}
if(i + slow <= n) {
add(n + i, i + slow, INF, sc);
}
} LL cost;
solve(s, t, cost);
printf("%lld", cost);
return ;
}
AC代码
②〇数字梯形问题。top
嗯...比较裸吧。(当年在湖南跟logeadd想了半天没想出来...)
第一问，全部INF，跑费用流。
第二问，边流量为1，跑费用流。
第三问，点流量为1，跑费用流。
实现上每次重置了所有的流量。
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top = ; int e[N], d[N], pre[N], Time, flow[N], G[][], m, n, tot, ID[][];
std::queue<int> Q;
bool vis[M]; inline void add(int x, int y, int z, int w) {
top++;
edge[top].nex = e[x];
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
e[x] = top;
top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c) {
continue;
}
if(d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
pre[y] = i;
flow[y] = std::min(flow[x], edge[i].c);
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
return d[t] < INF; // error 0
} inline void update(int s, int t) {
int f = flow[t], i = pre[t];
while(t != s) {
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
i = pre[t];
}
return;
} int solve(int s, int t, int &cost) {
int ans = ;
cost = ;
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
update(s, t);
Time++;
}
return ans;
} inline int id(int x, int y) {
if(!ID[x][y]) {
ID[x][y] = ++tot;
}
return ID[x][y];
} inline void clear() {
memset(vis, , sizeof(vis));
return;
} int main() {
scanf("%d%d", &m, &n);
int lm = (n + m) * n;
for(int i = ; i <= n; i++) {
for(int j = ; j <= m - + i; j++) {
scanf("%d", &G[i][j]);
}
}
int s = N - , t = N - ;
// part 1 NO
for(int i = ; i < n; i++) {
for(int j = ; j <= m - + i; j++) {
add(id(i, j) + lm, id(i + , j), , );
add(id(i, j) + lm, id(i + , j + ), , );
}
}
for(int i = ; i <= n; i++) {
for(int j = ; j <= m - + i; j++) {
add(id(i, j), id(i, j) + lm, , -G[i][j]);
}
}
for(int i = ; i <= m; i++) {
add(s, id(, i), , );
}
for(int i = ; i <= n + m - ; i++) {
add(id(n, i) + lm, t, , );
} int cost;
solve(s, t, cost);
printf("%d\n", -cost); memset(vis, , sizeof(vis));
// part 2 CROSS+POINT
int temp = ;
for(int i = ; i < n; i++) {
for(int j = ; j <= m - + i; j++) {
edge[++temp].c = ;
edge[++temp].c = ;
edge[++temp].c = ;
edge[++temp].c = ;
}
}
for(int i = ; i <= n; i++) {
for(int j = ; j <= m - + i; j++) {
edge[++temp].c = INF;
edge[++temp].c = ;
}
}
for(int i = ; i <= m; i++) {
edge[++temp].c = ;
edge[++temp].c = ;
}
for(int i = ; i <= n + m - ; i++) {
edge[++temp].c = INF;
edge[++temp].c = ;
} solve(s, t, cost);
printf("%d\n", -cost); memset(vis, , sizeof(vis));
// part 3 CROSS
temp = ;
for(int i = ; i < n; i++) {
for(int j = ; j <= m - + i; j++) {
edge[++temp].c = INF;
edge[++temp].c = ;
edge[++temp].c = INF;
edge[++temp].c = ;
}
}
for(int i = ; i <= n; i++) {
for(int j = ; j <= m - + i; j++) {
edge[++temp].c = INF;
edge[++temp].c = ;
}
}
for(int i = ; i <= m; i++) {
edge[++temp].c = ;
edge[++temp].c = ;
}
for(int i = ; i <= n + m - ; i++) {
edge[++temp].c = INF;
edge[++temp].c = ;
} solve(s, t, cost);
printf("%d\n", -cost); return ;
}
AC代码
②①家园。top
动态加点最大流。
唔......一开始看着有点像状压，发现不对，人有50个呢...
决定用一流量表示一个人。
然后飞船就用边表示，载客上限即为流量。
那么如何保证时间呢？自然想到了分层次，动态加边...(也可以二分)。
实现上就是枚举时间T，然后每次把飞船路径的两个点分层连起来。
然后跑最大流，如果超过k了就可以。
有个小坑，就是点必须分层，不能只用n个点。否则后面会搞不清时间先后顺序，导致你先走靠后时刻的边再走靠前时刻的边...
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cstring> const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c;
}edge[M << ]; int top = ; struct Ship {
int val, cnt;
int a[];
}sh[]; int e[N], d[N], n;
std::queue<int> Q; inline void add(int x, int y, int z) {
//printf("add : %d %d \n", x, y); top++;
edge[top].v = y;
edge[top].c = z;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool BFS(int s, int t) {
memset(d, , sizeof(d));
d[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[y]) {
continue;
}
d[y] = d[x] + ;
Q.push(y);
}
}
return d[t];
} int DFS(int x, int t, int maxF) {
if(x == t) {
return maxF;
}
int ans = ;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(!edge[i].c || d[x] + != d[y]) {
continue;
}
int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
if(!temp) {
d[y] = ;
}
ans += temp;
edge[i].c -= temp;
edge[i ^ ].c += temp;
if(ans == maxF) {
break;
}
}
return ans;
} inline int solve(int s, int t) {
int ans = ;
while(BFS(s, t)) {
ans += DFS(s, t, INF);
}
return ans;
} namespace ufs {
int fa[N];
inline int pre() {
for(int i = ; i < N; i++) {
fa[i] = i;
}
return ;
}
int odpa = pre();
int find(int x) {
if(x == fa[x]) {
return x;
}
return fa[x] = find(fa[x]);
}
inline void merge(int x, int y) {
fa[find(x)] = find(y);
return;
}
inline bool check(int x, int y) {
return find(x) == find(y);
}
} inline int id(int x, int deep) {
if(x == N - || x == N - ) {
return x;
}
return deep * n + x;
} int main() {
int m, k, s = N - , t = N - ;
scanf("%d%d%d", &n, &m, &k);
for(int i = ; i <= m; i++) {
scanf("%d%d", &sh[i].val, &sh[i].cnt);
for(int j = ; j < sh[i].cnt; j++) {
scanf("%d", &sh[i].a[j]);
if(sh[i].a[j] == ) {
sh[i].a[j] = s;
}
else if(sh[i].a[j] == -) {
sh[i].a[j] = t;
}
ufs::merge(sh[i].a[], sh[i].a[j]);
}
}
if(!ufs::check(s, t)) {
printf("");
return ;
}
// ----------- int ans = ;
for(int T = ; ; T++) {
//printf("T = %d ", T);
for(int i = ; i <= n; i++) {
add(id(i, T - ), id(i, T), INF);
} for(int i = ; i <= m; i++) {
int turn = T % sh[i].cnt;
int last = turn - ;
if(last < ) {
last = sh[i].cnt - ;
}
add(id(sh[i].a[last], T - ), id(sh[i].a[turn], T), sh[i].val);
}
ans += solve(s, t);
//printf("ans = %d \n", ans);
if(ans >= k) {
printf("%d", T);
break;
}
} return ;
}
AC代码
②②火星探险问题。top
唯一的障碍就是输出方案.....
首先建图，如果是障碍就没有那个点。
然后从终点往前推，每次走BFS出一条流量，代表一个车的路径。
然后输出。(听起来好像很简单...)
一开始我比较脑残，预处理了一波不可能到的点，实际上它们根本不会有流量...(而且还搞出个bug来，害我出现负环)
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring> typedef int LL;
const int N = , M = ;
const LL INF = 0x3f3f3f3f; struct POI {
int x, y;
POI(int X, int Y) {
x = X;
y = Y;
}
}; struct Edge {
int nex, v;
LL len, c;
}edge[M << ]; int top = ; int e[N], pre[N], vis[N], Time, n, m, fr[][], eg[][], G[][];
LL d[N], flow[N], cnt[N];
std::queue<int> Q;
std::queue<POI> P; inline void add(int x, int y, LL z, LL w) {
/*if(x == 200 || y == 200) {
printf("add : %d %d \n", x, y);
}*/
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
//printf("%lld \n%lld \n\n", d[t], INF);
d[s] = ;
vis[s] = Time;
flow[s] = INF;
cnt[s] = ;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
/*if(x == 202) {
printf("x = 202 \n");
}*/
vis[x] = ;
//printf("d[%d] = %d \n", x, d[x]);
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c && d[y] > d[x] + edge[i].len) {
/*if(x == 202) {
printf("x = 202, y = %d \n", y);
}*/
//printf("x = %d, y = %d \n", x, y);
d[y] = d[x] + edge[i].len;
flow[y] = std::min(flow[x], edge[i].c);
pre[y] = i;
cnt[y] = cnt[x] + ;
/*if(cnt[y] > N) {
printf("ERROR!!\n");
}*/
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
/*if(y == 202) {
printf("y = 202 x = %d \n", x);
}*/
}
}
}
}
//printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
return d[t] < INF;
} inline void update(int s, int t) {
LL f = flow[t];
//printf("update : f = %lld \n", f);
while(s != t) {
//printf("t = %d \n", t);
int i = pre[t];
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
}
return;
} inline LL solve(int s, int t, LL &cost) {
LL ans = ;
cost = ;
memset(vis, , sizeof(vis));
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
//printf("f = %lld d = %lld \n", flow[t], d[t]);
//printf("cost = %lld \n", cost);
update(s, t);
Time++;
}
return ans;
} inline int id(int x, int y) {
return (x - ) * m + y;
} inline void out(int x) {
int i = , j = ;
while() {
if(G[i][j + ] == && G[i + ][j] == ) {
break;
}
if(G[i][j + ] == -) {
printf("%d %d\n", x, );
j++;
}
else {
printf("%d %d\n", x, );
i++;
}
}
return;
} inline void exout(int k) {
memset(fr, -, sizeof(fr)); // 1 -> 0 |
memset(eg, , sizeof(eg));
P.push(POI(n, m));
int lm = n * m;
while(!P.empty()) {
int x = P.front().x;
int y = P.front().y;
P.pop();
//printf("P : %d %d \n", x, y);
x = id(x, y);
if(x == ) {
break;
}
for(int i = e[x]; i; i = edge[i].nex) {
y = edge[i].v;
if(!edge[i].c || y == x + lm) {
continue;
}
y -= lm;
int tx = (y - ) / m + , ty = y % m;
if(!ty) {
ty = m;
}
if(eg[tx][ty]) {
continue;
}
//printf(" >>> y : %d %d \n", tx, ty);
if(y + == x) { // ->
fr[tx][ty] = ;
}
else { // |
fr[tx][ty] = ;
}
eg[tx][ty] = i;
P.push(POI(tx, ty));
}
}
int x = , y = ;
while(x != n || y != m) {
printf("%d %d\n", k, fr[x][y]);
edge[eg[x][y]].c--;
if(fr[x][y] == ) {
y++;
}
else {
x++;
}
}
return;
} int main() { int k;
scanf("%d%d%d", &k, &m, &n);
for(int i = ; i <= n; i++) {
for(int j = ; j <= m; j++) {
scanf("%d", &G[i][j]);
}
}
for(int i = ; i <= n; i++) {
G[i][m + ] = ;
}
for(int i = ; i < m; i++) {
G[n + ][i] = ;
} for(int i = n; i >= ; i--) {
for(int j = m; j >= ; j--) {
bool f1 = G[i][j + ] == || G[i][j + ] == -;
bool f2 = G[i + ][j] == || G[i + ][j] == -;
if(f1 && f2) {
G[i][j] = -;
}
}
} /*puts("");
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
printf("%3d", G[i][j]);
}
puts("");
}*/ if(G[][] == || G[][] == -) {
for(int i = ; i <= k; i++) {
out(i);
}
return ;
}
int lm = n * m;
int s = lm * + , t = lm * + ;
for(int i = ; i <= n; i++) {
for(int j = ; j <= m; j++) {
if(G[i][j] == - || G[i][j] == ) {
continue;
}
int a = id(i, j);
if(G[i + ][j] != - && G[i + ][j] != && i < n) {
add(lm + a, id(i + , j), INF, );
}
if(G[i][j + ] != - && G[i][j + ] != ) {
add(lm + a, id(i, j + ), INF, );
}
if(G[i][j] == ) {
add(a, lm + a, , -);
}
add(a, lm + a, INF, );
}
}
add(s, , k, );
add(lm + lm, t, INF, ); int ans = solve(s, t, lm);
//printf("%d %d \n", ans, lm);
for(int i = ; i <= k; i++) {
exout(i);
} return ;
}
AC代码
②③航空路线问题。top
A->B->C的路径，可以转化为B->A和B->C两条。
然后用费用流搞一个经过城市最多的出来，输出方案。
注意：一条航线流量不能为1，因为可能被走两次，看这个SB样例：
2 1
a
b
a b
显然是有解的......
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
#include <map>
#include <string>
#include <iostream> typedef int LL;
using std::string;
const int N = , M = , INF = 0x3f3f3f3f; struct Edge {
int nex, v, c, len;
}edge[M << ]; int top = ; int e[N], d[N], vis[N], nex[N], pre[N], flow[N], Time;
std::queue<int> Q;
std::map<string, int> mp;
string str[N]; inline void add(int x, int y, LL z, LL w) {
top++;
edge[top].v = y;
edge[top].c = z;
edge[top].len = w;
edge[top].nex = e[x];
e[x] = top; top++;
edge[top].v = x;
edge[top].c = ;
edge[top].len = -w;
edge[top].nex = e[y];
e[y] = top;
return;
} inline bool SPFA(int s, int t) {
memset(d, 0x3f, sizeof(d));
//printf("%lld \n%lld \n\n", d[t], INF);
d[s] = ;
vis[s] = Time;
flow[s] = INF;
Q.push(s);
while(!Q.empty()) {
int x = Q.front();
Q.pop();
vis[x] = ;
//printf("d[%d] = %lld \n", x, d[x]);
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i].c && d[y] > d[x] + edge[i].len) {
d[y] = d[x] + edge[i].len;
flow[y] = std::min(flow[x], edge[i].c);
pre[y] = i;
if(vis[y] != Time) {
vis[y] = Time;
Q.push(y);
}
}
}
}
//printf("d < INF d = %lld %d \n", d[t], d[t] < INF);
return d[t] < INF;
} inline void update(int s, int t) {
LL f = flow[t];
//printf("update : f = %lld \n", f);
while(s != t) {
//printf("t = %d \n", t);
int i = pre[t];
edge[i].c -= f;
edge[i ^ ].c += f;
t = edge[i ^ ].v;
}
return;
} inline LL solve(int s, int t, LL &cost) {
LL ans = ;
cost = ;
memset(vis, , sizeof(vis));
Time = ;
while(SPFA(s, t)) {
ans += flow[t];
cost += flow[t] * d[t];
//printf("f = %lld d = %lld \n", flow[t], d[t]);
//printf("cost = %lld \n", cost);
update(s, t);
Time++;
}
return ans;
} int main() {
int n, m;
scanf("%d%d", &n, &m);
int s = n + n + , t = n + n + ;
for(int i = ; i <= n; i++) {
std::cin >> str[i];
mp[str[i]] = i;
add(i, i + n, (i == || i == n) ? : , -);
}
for(int i = ; i <= m; i++) {
std::cin >> str[];
int x = mp[str[]];
std::cin >> str[];
int y = mp[str[]];
if(x > y) {
std::swap(x, y);
}
add(y + n, x, , );
}
add(s, n, , );
add(n + , t, , ); int cost;
int ans = solve(s, t, cost); if(ans != ) {
printf("No Solution!");
return ;
} printf("%d\n", - - cost);
int x = ;
while(x != n) {
std::cout << str[x] << std::endl;
for(int i = e[x]; i; i = edge[i].nex) {
int y = edge[i].v;
if(y - n > x && edge[i].c) {
x = y - n;
edge[i].c--;
edge[i ^ ].c++;
break;
}
}
}
while(x != ) {
std::cout << str[x] << std::endl;
for(int i = e[x + n]; i; i = edge[i].nex) {
int y = edge[i].v;
if(edge[i ^ ].c && y < x) {
x = y;
break;
}
}
}
std::cout << str[x];
return ;
}
AC代码
②④机器人路径规划问题。top
cjk有个题解......光是看一眼就头大，先放着吧...
网络流的解法还没找到。
EX:网络流好难啊！！!!!!
网络流24题 gay题报告的更多相关文章
- COGS743. [网络流24题] 最长k可重区间集
743. [网络流24题] 最长k可重区间集 ★★★ 输入文件:interv.in 输出文件:interv.out 简单对比时间限制:1 s 内存限制:128 MB «问题描述: «编 ...
- Cogs 14. [网络流24题] 搭配飞行员
这道题其实蛮好想的,因为分为正,副飞行员.所以就把正飞行员当作Boy,副飞行员当作Girl.然后做Hungry即可. #include<bits/stdc++.h> using names ...
- 【线性规划与网络流 24题】已完成(3道题因为某些奇怪的原因被抛弃了QAQ)
写在前面:SDOI2016 Round1滚粗后蒟蒻开始做网络流来自我拯救(2016-04-11再过几天就要考先修课,现在做网络流24题貌似没什么用←退役节奏) 做的题目将附上日期,见证我龟速刷题. 1 ...
- cogs_14_搭配飞行员_(二分图匹配+最大流,网络流24题#01)
描述 http://cojs.tk/cogs/problem/problem.php?pid=14 有一些正飞行员和副飞行员,给出每个正飞行员可以和哪些副飞行员一起飞.一架飞机上必须一正一副,求最多多 ...
- BZOJ_1221_ [HNOI2001]_软件开发(最小费用流,网络流24题#10)
描述 http://www.lydsy.com/JudgeOnline/problem.php?id=1221 n天,每天需要r个毛巾,用完以后可以洗,要么花fa洗a天,要么花fb洗b天,毛巾不够了可 ...
- 【网络流24题】 No.12 软件补丁问题（最小转移代价 最短路）
[题意] T 公司发现其研制的一个软件中有 n 个错误, 随即为该软件发放了一批共 m 个补丁程序. 每一个补丁程序都有其特定的适用环境, 某个补丁只有在软件中包含某些错误而同时又不包含另一些错误时才 ...
- 【网络流24题】No.1 搭配飞行员(飞行员配对方案问题)
[问题描述] 飞行大队有若干个来自各地的驾驶员,专门驾驶一种型号的飞机,这种飞机每架有两个驾驶员,需一个正驾驶员和一个副驾驶员.由于种种原因,例如相互配合的问题,有些驾驶员不能在同一架飞机上飞 ...
- CJOJ 1494 【网络流24题】 搭配飞行员（二分图最大匹配）
CJOJ 1494 [网络流24题] 搭配飞行员(二分图最大匹配) Description 飞行大队有若干个来自各地的驾驶员,专门驾驶一种型号的飞机,这种飞机每架有两个驾驶员,需一个正驾驶员和一个副驾 ...
- [COGS 0014][网络流24题] 搭配飞行员
先贴题面 14. [网络流24题] 搭配飞行员 ★★☆ 输入文件:flyer.in 输出文件:flyer.out简单对比时间限制:1 s 内存限制:128 MB [问题描述] 飞行 ...
随机推荐
- mybtis逆向工程实战教程--条件查询
mabitis逆向工程进行条件查询:
- 基于vue-cli，sass，vant的移动端项目
项目架构 开始 vue init webpack 项目名称 //新建项目,cd进入新项目 npm install axios //先安装! ...
- MRP设置自动执行
1.在计划向导中,找到调度运算,如下配置, 2.配置成功后自动生成执行计划
- RocketMQ消息队列安装
一.官方安装文档 http://rocketmq.apache.org/docs/quick-start/ 下载地址 https://github.com/apache/rocketmq/releas ...
- Object...与Object[]使用的一点区别和记录
Object是所有类的基类 简述: Object ...objects(称为可变个数的形参)这种参数定义是在不确定方法参数的情况下的一种多态表现形式.Java可变参数,即这个方法可以传递多个参数,这个 ...
- Vue之v-for、v-show使用举例
demo.html <!DOCTYPE html> <html lang="en" xmlns:v-bind="http://www.w3.org/19 ...
- PHP超级全局变量、魔术变量和魔术函数
PHP超级全局变量(9个) $GLOBALS 储存全局作用域中的变量 $_SERVER 获取服务器相关信息 $_REQUEST 获取POST和GET请求的参数 $_POST 获取表单的POST请求参数 ...
- Quick Introduction to SQL Server Profiler
Introduction to Profiler SQL Server Profiler — or just Profiler — is a tool that can help monitor al ...
- A Simple Problem with Integers（线段树区间更新模板）
最基本的线段树的区间更新及查询和 用tag(lazy)数组来“延缓”更新,查询或添加操作必须进行pushdown操作,即把tag从p传到lp和rp并清楚tag[p],既然得往lp和rp递归,那么就可以 ...
- EasyUI-datebox设置开始日期小于结束日期，并且结束日期小于当前日期
datebox设置开始日期小于结束日期,并且结束日期小于当前日期 //日期控制扩展选择日期小于等于当前日期,开始日期小于等于结束日期 $("#datebox1").datebox( ...