清北澡堂 Day2 上午 一些比较重要的关于数论的知识整理

1.算数基本定理：

对于任意的大于1的正整数N，N一定能够分解成有限个质数的乘积，即

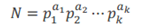
其中P1<P2<...<Pk,a₁,a₂,...,a_k>=1;

证：

存在性：

若存在最小的N不满足条件，当N为质数是，显然不成立；当N为合数时，存在P，使得N=P*（N/P），N/P<N,与假设N为最小的矛盾，故一定存在；

即：假设N为最小的

当N为质数直接gg

当N为合数还是gg

故不存在...

唯一性：

假设N的分解不唯一

设存在最小的N，使得N=p₁^r1 p₂^r2  .... p_k^rk且N=q₁t1  q₂t2 .....q_ntn

则p₁|q₁^t1  q₂^t2 .....q_n^tn

假设p₁=q₁,且r1>=t1，那么两个式子同时除以p₁^t1，

有p_{1^r1-t1.....=}q₁0  .....

而经过变换后的式子要小于原式

这与假设N为最小的不满足的矛盾

（A是一个<=n的正整数     两个条件至少有一个成立）

2.素数的判定

Miller-rabin素性测试

如果n为素数，取a<n，设n-1=d*2^r,则要么a^d≡1（mod n）要么存在0<=i<r,使得a^{d*2^t}≡-1(mod n)，要么存在0<=i<r，使得a^{d*2^t}≡-1(mod n)(有可能都满足)

任意一个a，如果满足这两个条件，n有可能是质数

     但a如果不满足这两个条件中的任何一个，它一定不是质数

     找k个a，如果都满足这两个条件，k-1个“更”有可能是质数

如果n是素数，取a<n,舍n-1=d*2^r,则要么a^d≡1(mod n),要么存在0<=i<r，使得a

选2,3,5,7,13,29,37,89，int范围内不可能出错

部分代码：

 int gg[]={,,,,,,,};

 long long kuaisumi(long long a,long long b1,long long c)
 {
     long long i=a;
     while(b1)
     {
         if(b1&)
         {
             s=(s*i)%c;
         }
         i=(i*i)%c;
         b1>>=;
     }
     return s%c;
 }

 bool miller_rabin(int a,int n)
 {
     int d=n-,r=;
     while(d%==)
         d/=,r++;
     int x=kuaisumi(a,d,n);
     if(x==)return true;
     for(int i=;i<r;i++)
     {
         if(x==n-)return true ;
         x=(long long )x*x%n;
     }
     return false;//可以对照素性测试看
 }

 bool is_prime (int n)
 {
     if(n<=)return false ;
     for(int a=;a<;a++)
         if(n==gg[a])return true;//一个个试
     for(int a=;a<;a++)
         if(!miller_rabin(gg[a],n))return false;
     return true;
 }

3，最大公因数

Gcd(a,b)=max{x(x|a,x|b)}

欧几里得算法的核心思想

gcd(a,b)=gcd(b,a-b)==>gcd(a,b)=gcd(b,a%b)

4.裴蜀定理

给定a,b,c,则ax+by=c有整数解的充要条件是gcd(a,b)|c

来证一下

不妨使用唯一分解定理

充分性：

d=gcd(a,b),

则d|a,d|b==>d|ax+by=c==>d|c充分性证毕

必要性：

设d=gcd(a,b),s=min(ax+by),s>0

a/s=q......r(0<=r<s)==>r=a-qs=a-q(ax+by)=(1-qx)a-qyb

因为s=min(ax+by)，所以r=0==>s|a&&s|b==>

1-------s|gcd(a,b)

s=ax+by=b(nd)+y(md)==>

2-------d|s

综合1,2，得到s=d

证毕

一个应用

请证明：设p为质数，若p|ab,则p|a或p|b

证：

当p|a时，显然成立

否则，gcd(p,a)=1==>xp+ya=1

b=b*1=b(xp+ya)=pxb+yab

p|pxb==>p|yab

5.拓展欧几里得

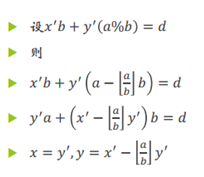
6.中国剩余定理

x≡a1(mod p₁)   x≡a2(mod p₂)   O(min(p1,p2))

x=a1,a1+p1,a1+2p2....,x<=a1+p2p1

过不了的情况：k=2,两个数都在1e9左右