c/c++ 用克鲁斯卡尔（kruskal）算法构造最小生成树

c/c++ 用克鲁斯卡尔（kruskal）算法构造最小生成树

最小生成树（Minimum Cost Spanning Tree）的概念：

假设要在n个城市之间建立公路，则连通n个城市只需要n-1条线路。这时，自然会考虑，如何在最节省经费的前提下建立这个公路网络。

每2个城市之间都可以设置一条公路，相应地都要付出一定的经济代价。n个城市之间，最多可以设置n(n-1)/2条线路，那么，如何在这些可能的线路中选择n-1条，以使总的耗费最少？

克鲁斯卡尔（kruskal）算法的大致思路：

把每条边的权重按照从小到大排序后，连接。连接时，需要查看要连接的两个顶点的父节点是否相同，不同才可以连接，连接后，更新父节点。

图为下图：

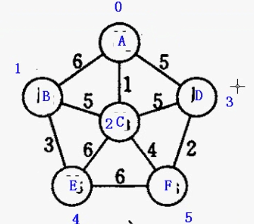
第一步

图1

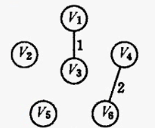
第二步

图2

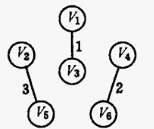
第三步

图3

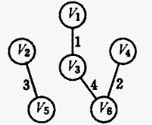
第四步

A->D,C->D,B->C的权重都是5，这时就不知道连哪个了，所以要创建2个辅助函数is_same,mark_same。

is_same用来判断要连接的2个点的父节点是否相同，如果相同就说明了，连接后，图就存在了环，所以不可以连接，放弃这条边，去寻找下一条边。

mark_same用来更新节点的父节点。

当拿到的节点是AD时，发现AD的父节点都是A，所以放弃；

当拿到的节点是CD时，发现AD的父节点都是A，所以放弃；

当拿到的节点是BC时，发现B的父节点是自己，C的父节点是A，父节点不同，所以连接，并更父节点

图4

找一半的矩阵，把各条边的起点，终点，权重，放到edge数组里

图5

mixSpanTree.h

#ifndef __mixspantree__
#define __mixspantree__

#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#include <memory.h>
#include <stdlib.h>
#include <stdbool.h>

#define Default_vertex_size 20

#define T char//dai biao ding dian de lei xing
#define E int
#define MAX_COST 0x7FFFFFFF

typedef struct GraphMtx{
  int MaxVertices;//zui da ding dian shu liang]
  int NumVertices;//shi ji ding dian shu liang
  int NumEdges;//bian de shu lian

  T* VerticesList;//ding dian list
  int** Edge;//bian de lian jie xin xi, bu shi 0 jiu shi 1
}GraphMtx;

typedef struct Edge{
  int begin;//边的起点
  int end;  //边的终点
  E   cost; //边的权重
}Edge;

//chu shi hua tu
void init_graph(GraphMtx* gm);
//打印二维数组
void show_graph(GraphMtx* gm);
//插入顶点
void insert_vertex(GraphMtx* gm, T v);
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost);

//用kruskal算法构造最小生成树
void minSpanTree_kruskal(GraphMtx* gm);

#endif

mixSpanTree.c

#include "mixSpanTree.h"

void init_graph(GraphMtx* gm){
  gm->MaxVertices = Default_vertex_size;
  gm->NumEdges = gm->NumVertices = 0;

  //kai pi ding dian de nei cun kong jian
  gm->VerticesList = (T*)malloc(sizeof(T) * (gm->MaxVertices));
  assert(NULL != gm->VerticesList);

  //创建二维数组
  //让一个int的二级指针，指向一个有8个int一级指针的数组
  //开辟一个能存放gm->MaxVertices个int一级指针的内存空间
  gm->Edge = (int**)malloc(sizeof(int*) * (gm->MaxVertices));
  assert(NULL != gm->Edge);
  //开辟gm->MaxVertices组，能存放gm->MaxVertices个int的内存空间
  for(int i = 0; i < gm->MaxVertices; ++i){
    gm->Edge[i] = (int*)malloc(sizeof(int) * gm->MaxVertices);
  }
  //初始化二维数组
  //让每个顶点之间的边的关系都为不相连的
  for(int i = 0; i < gm->MaxVertices; ++i){
    for(int j = 0; j < gm->MaxVertices; ++j){
      if(i == j)
	gm->Edge[i][j] = 0;
      else
	gm->Edge[i][j] = MAX_COST;
    }
  }
}
//打印二维数组
void show_graph(GraphMtx* gm){
  printf("  ");
  for(int i = 0; i < gm->NumVertices; ++i){
    printf("%c  ", gm->VerticesList[i]);
  }
  printf("\n");
  for(int i = 0; i < gm->NumVertices; ++i){
    //在行首,打印出顶点的名字
    printf("%c:", gm->VerticesList[i]);
    for(int j = 0; j < gm->NumVertices; ++j){
      if(gm->Edge[i][j] == MAX_COST){
	printf("%c  ", '*');
      }
      else{
	printf("%d  ", gm->Edge[i][j]);
      }
    }
    printf("\n");
  }
  printf("\n");
}
//插入顶点
void insert_vertex(GraphMtx* gm, T v){
  //顶点空间已满，不能再插入顶点了
  if(gm->NumVertices >= gm->MaxVertices){
    return;
  }
  gm->VerticesList[gm->NumVertices++] = v;
}

int getVertexIndex(GraphMtx* gm, T v){
  for(int i = 0; i < gm->NumVertices; ++i){
    if(gm->VerticesList[i] == v)return i;
  }
  return -1;
}
//添加顶点间的线
void insert_edge(GraphMtx* gm, T v1, T v2, E cost){
  if(v1 == v2)return;

  //查找2个顶点的下标
  int j = getVertexIndex(gm, v1);
  int k = getVertexIndex(gm, v2);
  //说明找到顶点了,并且点之间还没有线
  if(j != -1 && k != -1 ){
    //因为是无方向，所以更新2个值
    gm->Edge[j][k] = gm->Edge[k][j] = cost;
    //边数加一
    gm->NumEdges++;
  }
}

//比较边的权重,本函数作为快速排序函数的参数来使用。
int cmp(const void* a, const void* b){
  return ((*(Edge*)a).cost - (*(Edge*)b).cost);
}
//判断参数的2个顶点的父节点是否相同
bool is_same(int* father, int begin, int end){
  while(father[begin] != begin){
    begin = father[begin];
  }
  while(father[end] != end){
    end = father[end];
  }
  return begin == end;
}
//找到end节点的父节点x，再找到begin节点的父节点y，更新x节点的父节点为y
void mark_same(int* father, int begin, int end){
  while(father[begin] != begin){
    begin = father[begin];
  }
  while(father[end] != end){
    end = father[end];
  }
  father[end] = begin;

}
//用kruskal算法构造最小生成树
void minSpanTree_kruskal(GraphMtx* g){

  int n = g->NumVertices;
  Edge* edge = (Edge*)malloc(sizeof(Edge) * n*(n-1)/2);
  assert(edge != NULL);

  int k = 0;
  //查找一半的矩阵，把各条边的起点，终点，权重，放到edge数组里，参照上面的图5
  for(int i = 0; i < n; ++i){
    for(int j = i; j < n; j++){
      if(g->Edge[i][j] != 0 && g->Edge[i][j] != MAX_COST){
	edge[k].begin = i;
	edge[k].end = j;
	edge[k].cost = g->Edge[i][j];
	k++;
      }
    }
  }

  //按照权重来排序(用系统函数）
  //第一个参数：要被排序的数组
  //第二个参数：数组中元素的个数
  //第三个参数：每个数组元素占用的内存空间
  //第四个参数：函数指针，指定排序的规则
  qsort(edge, k, sizeof(Edge), cmp);

  //初始化每个节点的父节点，让每个节点的父节点为自身
  int *father = (int*)malloc(sizeof(int) * n);
  assert(NULL != father);
  for(int i = 0; i < n; ++i){
    father[i] = i;
  }

  for(int i = 0; i < n; ++i){
    //判断2个节点的父节点是否相同，不相同就连接
    if(!is_same(father, edge[i].begin, edge[i].end)){
      printf("%c->%c:%d\n",g->VerticesList[edge[i].begin],g->VerticesList[edge[i].end], edge[i].cost);
      //连接后，找到节点end的父节点x，再找到节点begin的父节点y，把节点x的父节点更新为y
      mark_same(father, edge[i].begin, edge[i].end);
    }
  }
}

mixSpanTreemain.c

#include "mixSpanTree.h"

int main(){
  GraphMtx gm;
  //初始化图
  init_graph(&gm);
  //插入顶点
  insert_vertex(&gm, 'A');
  insert_vertex(&gm, 'B');
  insert_vertex(&gm, 'C');
  insert_vertex(&gm, 'D');
  insert_vertex(&gm, 'E');
  insert_vertex(&gm, 'F');

  //添加连线
  insert_edge(&gm, 'A', 'B', 6);
  insert_edge(&gm, 'A', 'D', 5);
  insert_edge(&gm, 'A', 'C', 1);
  insert_edge(&gm, 'B', 'E', 3);
  insert_edge(&gm, 'B', 'C', 5);
  insert_edge(&gm, 'C', 'E', 6);
  insert_edge(&gm, 'C', 'D', 5);
  insert_edge(&gm, 'C', 'F', 4);
  insert_edge(&gm, 'F', 'E', 6);
  insert_edge(&gm, 'D', 'F', 2);
  //打印图
  show_graph(&gm);

  //kruskal
  minSpanTree_kruskal(&gm);

}

完整代码

编译方法：gcc -g mixSpanTree.c mixSpanTreemain.c