洛谷P2421 [NOI2002]荒岛野人(扩展欧几里得)

题目背景

原 A-B数对（增强版）参见P1102

题目描述

克里特岛以野人群居而著称。岛上有排列成环行的M个山洞。这些山洞顺时针编号为1,2,…,M。岛上住着N个野人，一开始依次住在山洞C1,C2,…,CN中，以后每年，第i个野人会沿顺时针向前走Pi个洞住下来。

每个野人i有一个寿命值Li，即生存的年数。

下面四幅图描述了一个有6个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为1，2，3；每年要走过的洞穴数依次为3，7，2；寿命值依次为4，3，1。

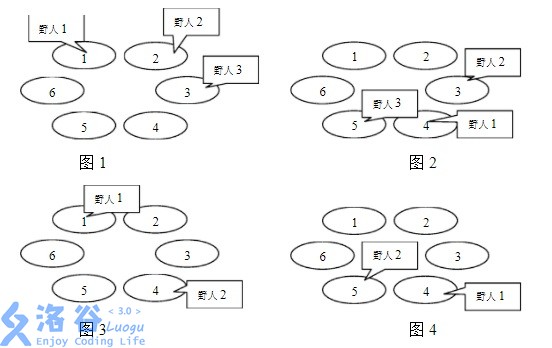
奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

输入输出格式

输入格式：

第1行为一个整数N(1<=N<=15)，即野人的数目。

第2行到第N+1每行为三个整数Ci, Pi, Li (1<=Ci,Pi<=100, 0<=Li<=106 )，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

输出格式：

仅包含一个数M，即最少可能的山洞数。输入数据保证有解，且M不大于10^6。

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

对于50% 的数据：N 的范围是[1…1,000]。

对于另外50% 的数据：N 的范围是[1…100,000]。

对于100% 的数据：C 的范围是[1…1,000,000,000]，N 个整数中每个数的范围是：[0…1,000,000,000]。

我居然切了一道紫题？？！！好开心qwq

设第$i$个人的寿命为$x_i$，每次走$y_i$，刚开始在$a$，

若洞穴数为$b$，那么我们需要找到最小的$b$满足对于任意的两个野人$i,j$

$a_i+y_i * T_i \not \equiv a_j + y_j + T_j \pmod b$，$T$表示第几年。

然后这个是个标准的欧几里得式子

枚举一个$b$，判断就好了

#include<cstdio>

#include<cstring>

#include<algorithm>

#include<cmath>

using namespace std;

const int MAXN = , B = ;

inline int read() {

    char c = getchar(); int x = , f = ;

    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}

    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();

    return x * f;

}

int N;

struct Node {

    int bg, step, life;

    bool operator < (const Node &rhs) const {

        return this -> step < rhs.step;

    }

}a[MAXN];

int x, y;

int exgcd(int a, int b, int &x, int &y) {

    if(b == ) {

        x = , y = ; return a;

    }

    int r = exgcd(b, a % b, x, y);

    int tmp = x; x = y, y = tmp - (a / b) * y;

    return r;

}

bool check(int X) {

    for(int i = ; i <= N; i++) {

        for(int j = ; j <= i - ; j++) {

            int B = X;

            int A = a[i].step - a[j].step, C = a[j].bg - a[i].bg, r = __gcd(A, B);

            if(C % r != ) continue;

            A = A / r; B = B / r; C = C / r;

            exgcd(A, B, x, y);

            x = (x * C) % B;

            while(x < ) x += B;

            if(x <= a[i].life && x <= a[j].life) return ;

        }

    }

    return ;

}

main() {

#ifdef WIN32

    freopen("a.in", "r", stdin);

#endif

    N = read();

    int fuck = ;

    for(int i = ; i <= N; i++)

        a[i].bg = read(), a[i].step = read(), a[i].life = read(),

        fuck = max(fuck, a[i].bg);

    sort(a + , a + N + );

    for(int i = fuck; i <= 1e6; i++)//一定要从最大值开始，，好坑。。

        if(check(i))

            {printf("%d\n", i); exit();}

}