贝叶斯推断之最大后验概率(MAP)

贝叶斯推断之最大后验概率(MAP)

本文详细记录贝叶斯后验概率分布的数学原理，基于贝叶斯后验概率实现一个二分类问题，谈谈我对贝叶斯推断的理解。

1. 二分类问题

给定N个样本的数据集，用\(X\)来表示，每个样本\(x_n\)有两个属性，最终属于某个分类\(t\)

\(t=\left\{0,1\right\}\)

\(\mathbf{x_n}=\begin{pmatrix}x_{n1} \\ x_{n2} \\ \end{pmatrix}\)， 假设模型参数\(w=\begin{pmatrix} w_1 \\ w_2\end{pmatrix}\)

\(\mathbf{X}=\begin{bmatrix} x_1^T \\ x_2^T \\. \\. \\ x_n^T\end{bmatrix}\)

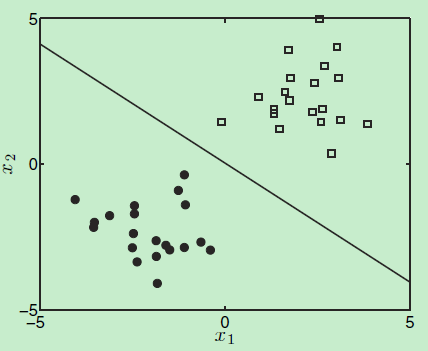
将样本集用用图画出来如下：

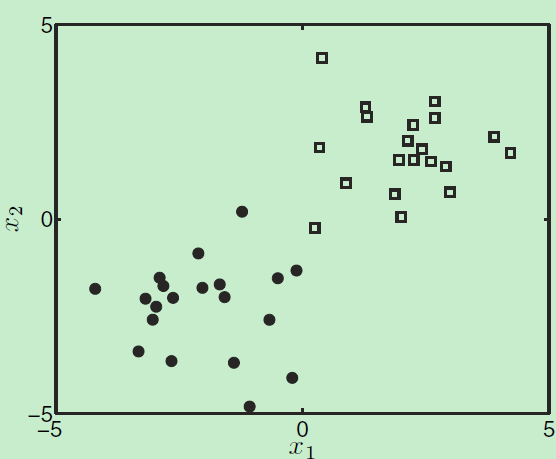
根据贝叶斯公式有：

\[p(w|t,X)=\frac {p(t|X,w)p(w)} {p(t|X)} \] (公式1)

\(p(w | t,X)\)告诉我们：在已知训练样本集 \(X\) 以及这些样本的某个分类 \(t\) (这是一个监督学习，因为我们已经有了样本集\(X\)、以及样本集中每个样本所属的分类\(t\))，需要求解模型参数 \(w\) 。因此，\(w\) 是未知的，是需要根据样本通过贝叶斯概率公式来进行求解的。求得了\(p(w|t,X)\)的分布，也就知道了模型参数\(w\)

当我们求得了最优的模型参数 \(w^*\) 之后，给定一个待预测的样本 \(\mathbf{x_{new}}\) 根据公式\[P(T_{new}=1|x_{new}, w^*)\] 来计算新样本 \(\mathbf{x_{new}}\) 归类为 1 的概率是多少，这就是模型的预测。

公式1 中等号右边一共有三部分，\(p(t|X,w)\)称为似然概率(likelihood)，\(p(w)\)称为先验概率，这两部分一般比较容易求解。最难求解的是分母: \(p(t|X)\) 称为边界似然函数(marginal likelihood)。但是幸运的是，边界似然函数与模型参数\(w\)无关，因此，可以将分母视为关于 \(w\) 的一个常量。

在数学上，若先验概率与似然概率共轭，那么后验分布概率\(p(w|t, X)\) 与先验概率服从相同的分布。比如说：先验概率服从Beta分布，似然概率服从二项分布，这时先验概率分布与似然概率分布共轭了，那么后验概率也服从Beta分布。

因此，在使用贝叶斯公式时，如果选择的先验概率分布与似然概率分布共轭，那后验概率分布就很容易计算出来了（或者说是能够准确地计算出一个 具体的/精确的 模型参数 \(w^*\)），这就是：can compute posterior analytically。但现实是，它们二者之间不共轭，从而出现了三种常用的近似计算方法：

• 点估计(Point Estimate--MAP方法)
• 拉普拉斯近似方法(Laplace approximation)
• 采样法(Sampling--Metropolis-Hastings)

而本文只介绍点估计法。

回到公式1，首先来看先验概率\(p(w)\) ，先验概率类似于在做一个决定时，已有的经验。因为我们已经有了训练样本\(X\)，将这些样本对应的等高线画出来，它们根高斯分布很接近，那么就可以认为先验概率服从高斯分布。也即\[p(w)=N(0,\sigma^2I)\]。其中，\(w\) 是一个向量，\(I\) 是单位矩阵。

接下来是似然概率 \(p(t|X,w)\) ，假设在给定模型参数\(w\) 以及样本集\(X\) 的条件下，各个样本的分类结果是相互独立的，因此：

\[p(t|X,w)=\prod_{n=1}^N p(t_n|x_n, w)\] (公式2)

举个例子，在已知模型参数 \(w\) 时，\(w\) 将\(x_1\) 预测为正类，将 \(x_2\) 预测为负类……将 \(x_n\) 预测正类，模型对各个样本的预测结果是相互独立的。即：\(w\) 对 \(x_1\) 的预测结果 不会影响它对 \(x_2\)的预测结果。

由于，是二分类问题，\(t_n=\left\{0,1\right\}\) ,可以进一步将公式2 写成：\[p(t|X,w)=\prod_{n=1}^N p(T_n=t_n|x_n, w)\] ，其中 \(T_n\) 代表样本\(x_n\)被归为某个类的 随机变量，\(t_n\)是该随机变量的取值。比如\(t_n=0\)表示样本\(x_n\)被分类为正类，\(t_n=1\)表示被归为负类。

2. sigmod函数

由于随机变量取某个值的概率在[0,1]之间，因此要求解\(p(t|X,w)\)，我们的目标是：找一个函数\(f(\mathbf{x_n};w)\) 这个函数能够产生一个概率值。为了简化讨论，选择 \(sigmod(w^T*x)\) ，于是：

\[P(T_n=1|x_n,w)=\frac{1}{1+exp(-w^T*x_n)}\]

那么：

\[P(T_n=0|x_n,w)=1-P(T_n=1|x_n,w)=\frac{exp(-w^T*x_n)}{1+exp(-w^T*x_n)}\]

将上面两个公式合二为一：

\[P(T_n=t_n|x_n,w)=P(T_n=1|x_n,w)^{t_n}P(T_n=0|x_n,w)^{1-t_n}\]

对于N个样本，公式2可写成：

\[p(t|X,w)=\prod_{n=1}^N (\frac{1}{1+exp(-w^T*x_n)})^{t_n}(\frac{exp(-w^T*x_n)}{1+exp(-w^T*x_n)})^{1-t_n}\] (公式3)

至此，先验概率服从高斯分布，似然概率由公式3 给出，就可以求解前面提到的后验概率公式：\[p(w|X,t,\sigma^2)\]

只要求得了后验概率，就可以使用如下公式计算新样本分为负类的概率：

\[P(t_{new}=1|x_{new}, X, t)=E_{p(w|X,t,\sigma^2)}\left(\frac{1}{1+exp(-w^T*x_{new})}\right)\]

解释一下这个公式：因为现在已经求得了后验概率\(p(w|X,t,\sigma^2)\)的表达式，它是一个关于\(f(x_n;w)\)的函数，计算这个函数的期望值\(E\)，这个期望值就是 预测新样本\(x_{new}=1\)的概率。

好，接下来就是求解后验概率了。

3. 求解后验概率

前面已经说过，先验概率服从高斯分布\(N(0,\sigma^2I)\)，似然分布由 公式3 给出，而分母--边界似然函数是一个关于 \(w\) 的常数，因此定义一个函数 \(g(w;X,t,\sigma^2)=p(t|X,w)p(w|\sigma^2)\) ，函数\(g\) 显然与后验概率\(p(w|X,t,\sigma^2)\)成比例。因此，求得了函数\(g\) 的最大值，就相当于求得了后验概率的最优参数\(w^*\)。

这里有个问题就是：凭什么能最大化函数g呢？\(g\)是 \(w\) 的函数，\(w\)取哪个值时函数 \(g\) 达到最大值呢？

这里需要用到一个方法叫做牛顿法(Newton-Raphson method)。牛顿法可用于寻找函数中的零点。它通过下面公式：

\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\]

不断迭代，最终找到函数值为0的点。

而在数学中判断函数在某个点取极值时，有如下定理：

以一元可导函数\(h(x)\)为例，\(h(x)\)导数为0的点是极值点，但是这个极值点是极小值，还是极大值呢？这时可通过判断\(h(x)\)是二阶导数来判断该极值点到底是极小值还是极大值。若\(h'(x_n)=0\)且\(h''(x_n)<0\)，则，则\(h(x)\)在在 \(x_n\)处取极大值。

因此，若能够判断 \(g(w;X,t,\sigma^2)\)关于\(w\)的二阶导数小于0，那么就可以使用牛顿法来求解 \(g(w;X,t,\sigma^2)\)的一阶导数关于\(w\)的零点，即\(g'(w;X,t,\sigma^2)=0\)时\(w\)的取值为\(w_0\)，这个\(w_0\)就是最优解 \(w^*\)了。

好，那下面就来证明一下\(g(w;X,t,\sigma^2)\)关于\(w\)的二阶导数是小于0的。由于\(w\)是向量，在多元函数中，相当于要证明的是：\(g(w;X,t,\sigma^2)\)关于\(w\)的黑塞矩阵是负定的。

将函数\(g\)取对数，最大化\(log (g(w;X,t,\sigma^2))\)

\(log (g(w;X,t,\sigma^2))=log({p(t|X,w)p(w|\sigma^2}))\)

\[=log(p(t|X,w)+log(p(w|\sigma^2)\]

为了简化公式，做如下约定：

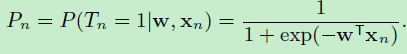
假设\(w\)是一个\(D\)维向量：

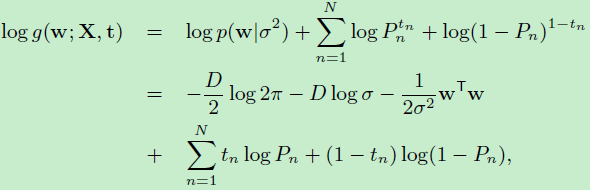
前面三项是先验分布服从高斯分布后，化简得到的结果。根据向量求导公式：\[\frac{\partial w^Tw}{\partial w}=w\]

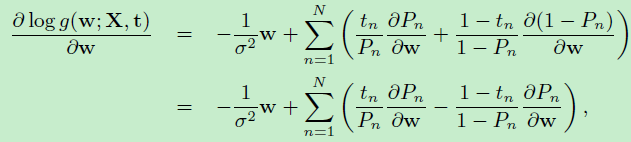
由链式求导法则：

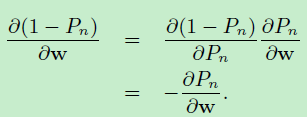
得到：

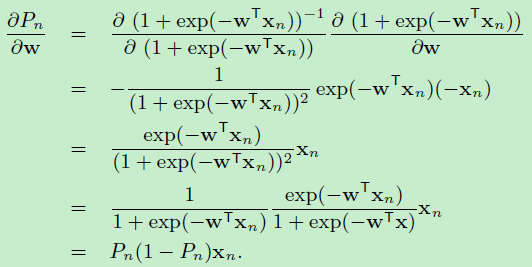
于是：\(log (g(w;X,t,\sigma^2))\)对 \(w\)的一阶偏数如下：

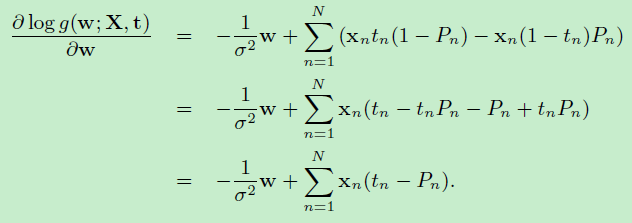
二阶偏导数如下：

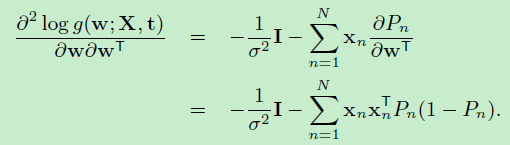
\(I\)是单位矩阵，\(0=<P_n<=1\)是概率值，求得的二阶偏导数就是黑塞矩阵，它是负定的。

证明完毕。

至此，就可以放心地用牛顿法不断迭代，找出\(g(w;X,t,\sigma^2)\)取最大值时参数\(w\)的值了，而这个值就是\(w^*\)

现在，\(w^*\)求出来了，就可以用下面公式预测新样本 \(x_{new}\)被预测为负类(\(T_{new}\)取值为1)的概率了

\[P(T_{new}=1|x_{new},w^*)=\frac{1}{1+exp(-w^{*T}x_{new})}\]

decision boundary

由于是个二分类问题，来看看使用贝叶斯后验概率进行分类的 决定边界 长什么样子。由于输出的是一个概率值，显然约定\(P(T_{new}=1|x_{new},w^*)>0.5\)预测为负类，\(P(T_{new}=1|x_{new},w^*)<0.5\)时预测为正类。那等于0.5时呢？

根据：\[P(T_{new}=1|x_{new},w^*)=\frac{1}{1+exp(-w^{*T}x_{new})}=0.5\]得出：

\[-w^{*T}*x=0=w_1^*x_1+w_2^*x_2\]

\[x_2=\frac{w_1^*}{w_2^*}*(-x_1)\]

也就是说样本\(\mathbf{x}=\begin{pmatrix}x_{1} \\ x_{2} \\ \end{pmatrix}\)的两个属性\(x_1\)和\(x_2\)是成线性比例的。而这条直线就是decision boundary

总结

贝叶斯方法是机器学习中常用的一种方法，在贝叶斯公式中有三部分，先验概率分布函数、似然概率分布函数、和边界似然概率分布函数（贝叶斯公式的分母）。求出了这三部分，就求得了后验概率分布，然后对于一个新样本\(x_{new}\)计算后验概率分布的期望值，这个期望值就是贝叶斯模型的预测结果。

由于后验概率分布的计算依赖于先验概率分布函数、似然概率分布函数，当这二者共轭时，后验概率与先验概率服从相同的分布函数，从而可以推导计算出后验概率分布(posterior could be computed analytically)。但是，当这二者不共轭时，则是计算后验概率分布的近似值。计算近似值一共有三种方法，点估计法(point estimate --- MAP)，拉普拉斯近似法，Metropolis-Hastings采样法。而本文主要介绍 是第一种方法：点估计法(point estimate --- maximum a posteriori)。

maximum a posteriori中的最大化体现在哪里呢？其实是体现在似然分布函数的最大化上。黑塞矩阵的负定性证明了\(g(w;X,t,\sigma^2)\)有最大值，再使用牛顿法不断迭代找到了这个使得函数\(g\)取最大值的最优参数解\(w^*\)。而求得了最优参数\(w^*\)，就求得了后验概率分布公式。对于一个待预测的新样本\(x_{new}\)，计算该样本后验概率分布的期望值，这个期望值就是贝叶斯模型对新样本的预测结果。

参考资料

牛顿法：https://zh.wikipedia.org/wiki/牛顿法
博客园Markdown公式乱码：http://www.cnblogs.com/cmt/p/markdown-latex.html

原文：http://www.cnblogs.com/hapjin/p/8834794.html