『嗨威说』算法设计与分析 - 贪心算法思想小结（HDU 2088 Box of Bricks）

本文索引目录：

一、贪心算法的基本思想以及个人理解

二、汽车加油问题的贪心选择性质

三、一道贪心算法题点拨升华贪心思想

四、结对编程情况

一、贪心算法的基本思想以及个人理解：

　　1.1　　基本概念：

　　首先我们从课本中仔细品读基本的贪心概念，顾名思义，贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。当然，希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。如单源最短路经问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。

　　因此对于贪心算法来说，这类算法没有固定的模板套路，当局部最优与全局最优解一致性被证明之后，即可使用贪心算法。

　　1.2　　使用条件：

　　（1）需要具有贪心选择性质

　　所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。

　　动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行，以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。

　　对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。

　　（2）需要具有最优子结构性质

　　当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

　　1.3　　使用思想：

　　贪心算法是从问题的某一个初始值出发并且不断接近所给定的特定目标，以尽可能快的地求得更好的解。当达到算法中的某一步不能再继续前进时，算法停止。但是贪心算法无法保证最后的解是最佳的，并且不能求解最大或最小解问题，只能求解满足某些约束条件的可行解的范围。

　　1.4　　贪心算法的经典问题种类：

（1）背包问题

（2）活动时间安排的问题

（3）线段覆盖问题

（4）数字组合问题

（5）最大整数问题

（6）均分纸牌问题

（7）找零钱问题

二、汽车加油问题的贪心选择性质：

　　PTA7-1 汽车加油问题：寻找汽车满油量时可以行驶的最大路程的最后一个加油站，并且加油后重置当前油量的变量，并且用一个ans标记变量增加次数，并继续用此方法前进，特别需要注意的是需要检查每一小段路程是否超过汽车满油量时的最大支撑路程。

三、一道贪心算法题点拨升华贪心思想：

　　2.1　　题目来源：

　　　　HDU：http://acm.hdu.edu.cn/showproblem.php?pid=2088

　　2.2　　题目题干：

　　Box of Bricks

·Problem Description：

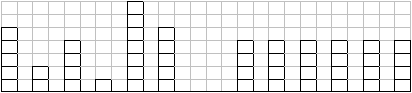
　　Little Bob likes playing with his box of bricks. He puts the bricks one upon another and builds stacks of different height. “Look, I've built a wall!”, he tells his older sister Alice. “Nah, you should make all stacks the same height. Then you would have a real wall.”, she retorts. After a little consideration, Bob sees that she is right. So he sets out to rearrange the bricks, one by one, such that all stacks are the same height afterwards. But since Bob is lazy he wants to do this with the minimum number of bricks moved. Can you help?

·Input

　　The input consists of several data sets. Each set begins with a line containing the number n of stacks Bob has built. The next line contains n numbers, the heights hi of the n stacks. You may assume 1≤n≤50 and 1≤hi≤100.
　　The total number of bricks will be divisible by the number of stacks. Thus, it is always possible to rearrange the bricks such that all stacks have the same height.
　　The input is terminated by a set starting with n = 0. This set should not be processed.

 

·Output

　　For each set, print the minimum number of bricks that have to be moved in order to make all the stacks the same height.
　　Output a blank line between each set.

 

·Sample Input

　　6

　　5 2 4 1 7 5

　　0

 

·Sample Output

　　5

　　2.3　　题目大意：

　　　　题目意思是：给定一堆积木，并且分成k列，试问如何用最少的移动操作（只能移动到相邻位置），能够将k列堆积木达到平均高度。

　　2.4　　题目思路：

　　　　本题的贪心性质选择为：计算出总共的砖块数，在求出N堆砖的平均高度(即需要达到的最终高度)，把高的堆上的砖移到不足平均高度的堆上。应该计算出所有不足高度的堆上总共差多少砖达到高度，即为结果。

 

　　2.5　　题目AC代码：

#include<stdio.h>
#include<string.h>

int main()
{
    int N;
    int a[];
    int kase = ;
    while(scanf("%d",&N) && N)
    {
        int sum = ;
        for(int i = ; i < N; i++)
        {
            scanf("%d",&a[i]);
            sum += a[i];
        }
        int ans = ;
        for(int i = ; i < N; i++)
        {
            if(a[i] < sum/N)
                ans += sum/N - a[i];
        }
        printf("Set #%d\n",kase++);
        printf("The minimum number of moves is %d.\n\n",ans);
    }

    return ;
}

四、 结对编程情况：

　　经过前几次实践题合作之后，结对编程逐渐顺利，能够让双方都能不断进行思路碰撞，实现较为合适的算法，当和三木小哥哥想到一起完成了算法设计、完成代码书写、成功AC一题之后，会有较为愉悦的心情感，较为顺利的完成三道题，继续加油，暂无较大问题。

如有不合理的地方，请及时指正，我愿听取改正~

参考链接：https://oi-wiki.org/